0

Guest

Courses New

2 pt charges +q and -2q are placed at the vertices of a eq. triangle ABC .obtain expression for the magnitude and direction of the resultant electric field at the vertex A due to these charges

2 pt charges +q and -2q are placed at the vertices of a eq. triangle ABC .obtain expression for the magnitude and direction of the resultant electric field at the vertex A due to these charges

Question Image
Grade:12

2 Answers

Samyak Jain
333 Points
4 years ago
You cannot perform scalar addition of two electric field vectors. You have to do vector sum of the vectors and
then find its magnitude.
Electric field at A due to charge q at B is along side AB and away from it and that at A due to carge – 2q ta C
is along side AC and towards it.
Their magnitudes are Kq / a2 and 2Kq / a2 assuming q to be a positive charge.
Electric field due to point charge q can be resolved as (Kq / a2)cos30\degree j + (Kq / a2)sin30\degree i
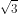
                                                                          = (Kq / 2a2) i + (\sqrt{3}Kq / 2a2) j.
Electric field due to point charge – 2q can be resolved as – (2Kq / a2)cos30\degree j + (2Kq / a2)sin30\degree i
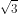
                                                                         = (Kq / a2) i  –  (\sqrt{3}Kq / a2) j.
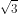
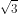
Their resultant is (Kq / 2a2) i + (\sqrt{3}Kq / 2a2) j + (Kq / a2) i  –  (\sqrt{3}Kq / a2) j
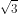
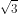
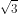                        =  (3Kq / 2a2) i  –  (\sqrt{3}Kq / 2a2) j  =  (\sqrt{3}Kq / 2a2)(\sqrt{3} i – j)
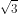
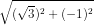
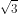
Magnitude of resultant  =  (\sqrt{3}Kq / 2a2)\sqrt{(\sqrt{3})^2 + (-1)^2}   =   (\sqrt{3}Kq / 2a2) . 2
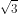                                      =  \sqrt{3}Kq / a2 .
Khimraj
3007 Points
4 years ago
Steps and Understanding :
1) We will find Electric Potential by writing V = K(q) / d 
where q is charge contained in ring. 
d - distance of charge from point .
k = 1/4π£° 
where £° is permitivity in vacuum. 
2) We will find Electric Field by 
E = -dV/dx 
 

Think You Can Provide A Better Answer ?

Other Related Questions on Electrostatics

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More