Other Related Questions on discuss with colleagues and iitians

Are core branches(Mechanical) in Top 3 NIT worth it ?
Are core branches(Mechanical) in Top 3 NIT worth it ?
discuss with colleagues and iitians
1 Answer Available
Last Activity: 3 Years ago

My rank in JEE Advanced 2022 is 1871. Should I go for IIT Guwahati ECE or IIT Kanpur Mechanical and try for a branch change to CS or Electrical Engineering? Is changing your branch very difficult?
My rank in JEE Advanced 2022 is 1871. Should I go for IIT Guwahati ECE or IIT Kanpur Mechanical and try for a branch change to CS or Electrical Engineering? Is changing your branch very difficult?
discuss with colleagues and iitians
1 Answer Available
Last Activity: 3 Years ago

Can i sacrifice board exams for jee mains as board exams are no where valueable as cuet and other will be seen for admission
Can i sacrifice board exams for jee mains as board exams are no where valueable as cuet and other will be seen for admission
discuss with colleagues and iitians
1 Answer Available
Last Activity: 3 Years ago

Is a student studying in IGCSE syllabus eligible for taking IOQP or IOQJS?
Is a student studying in IGCSE syllabus eligible for taking IOQP or IOQJS?
discuss with colleagues and iitians
1 Answer Available
Last Activity: 3 Years ago

I have wasted my 11th? Is it still possible to get into my dream iit? Do i have to cover 11 th syllabus first? When and how can i finish it?
I have wasted my 11th? Is it still possible to get into my dream iit? Do i have to cover 11 th syllabus first? When and how can i finish it?
discuss with colleagues and iitians
1 Answer Available
Last Activity: 3 Years ago





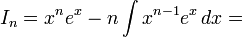

 .
.










