 Discuss with colleagues and IITians> Log...
Discuss with colleagues and IITians> Log...

 2 Answers
2 AnswersSudheesh Singanamalla
The logarithm (or log) of a number to a given base is the power to which the base must be raised in order to produce that number.
the logarithm of 1000 to base 10 is 3, because 10 to the power of 3 is 1000.



![\log_b(\sqrt[p]x) = \frac {\log_b x}p. \,](http://upload.wikimedia.org/math/5/6/a/56a5930f2ae7a5992baef464910df49a.png)
- lets take an example now,
- suppose we want to find the value of 3.055*6.225
- lets take log to the base 10 .
- log ( a * b ) = log a + log b
- ==> log(1.055 * 6.225) = log 3.055 + log 6.225
- to take log we take the number of integers before the decimal point and subtract it by 1.
- since there is 1 element before the decimal point it becomes 1-1 = 0
- therfore we write the value of log as 0. and then the number's log value.
- then in the log table we check for '30' in the 5th vertical column which gives the log of 3.05 since there is another 5 after this 3.05 , after the 10the vertical column there are small columns which have some values under the numbers 0-9.... check for the number 5 in this and add it to the value you found in 3.05
- therefore log 3.05 = 0.4843
- log 3.055 = 0.4850
- similarly find for the other number
- log 6.22 = log of 62 in the 2nd column (under the value 2)
- = 0.7938
- log 6.225 = 0.7941
- so now the values are 0.4850 and 0.7941
- so now add both of them that gives you the log value.
- so log ( 3.055 * 6.225 ) = 0.7941 + 0.4850 = 1.2791
- so that is the log value.
- now try this for yourself :
- find the log of (i) 5.226 * 41.25
- (ii) 22.47 * 33.11
- Please approve !
vijesh jayan
Two kinds of logarithms are often used in chemistry: common (or Briggian) logarithms and natural (or Napierian) logarithms. The power to which a base of 10 must be raised to obtain a number is called the common logarithm (log) of the number. The power to which the base e (e = 2.718281828.......) must be raised to obtain a number is called the natural logarithm (ln) of the number.
In simpler terms, my 8th grade math teacher always told me: LOGS ARE EXPONENTS!! What did she mean by that?
- Using log10 ("log to the base 10"):
log10100 = 2 is equivalent to 102 = 100
where 10 is the base, 2 is the logarithm (i.e., the exponent or power) and 100 is the number. - Using natural logs (loge or ln):
Carrying all numbers to 5 significant figures,
ln 30 = 3.4012 is equivalent to e3.4012 = 30 or 2.71833.4012 = 30 - Many equations used in chemistry were derived using calculus, and these often involved natural logarithms. The relationship between ln x and log x is:
ln x = 2.303 log x Why 2.303? Let's use x = 10 and find out for ourselves.
Rearranging, we have (ln 10)/(log 10) = number.
We can easily calculate that ln 10 = 2.302585093... or 2.303 and log 10 = 1.
So, the number has to be 2.303. Voila! - Historical note: Before calculators, we used slide rules (a tool based on logarithms) to do calculations requiring 3 significant figures. If we needed more than 3 signficant figures, we pulled out our lengthy logarithm tables. Anyway, enough history......
The rest of this mini-presentation will concentrate on logarithms to the base 10 (or logs). One use of logs in chemistry involves pH, where pH = -log10 of the hydrogen ion concentration.
FINDING LOGARITHMS
Here are some simple examples of logs.
| Number | Exponential Expression | Logarithm |
|---|---|---|
| 1000 | 103 | 3 |
| 100 | 102 | 2 |
| 10 | 101 | 1 |
| 1 | 100 | 0 |
| 1/10 = 0.1 | 10-1 | -1 |
| 1/100 = 0.01 | 10-2 | -2 |
| 1/1000 = 0.001 | 10-3 | -3 |
To find the logarithm of a number other than a power of 10, you need to use your scientific calculator or pull out a logarithm table (if they still exist). On most calculators, you obtain the log (or ln) of a number by
- entering the number, then
- pressing the log (or ln) button.
- Example 1: log 5.43 x 1010 = 10.73479983...... (way too many significant figures)
- Example 2: log 2.7 x 10-8 = -7.568636236...... (too many sig. figs.)
So, let's look at the logarithm more closely and figure out how to determine the correct number of significant figures it should have.
For any log, the number to the left of the decimal point is called the characteristic, and the number to the right of the decimal point is called the mantissa. The characteristic only locates the decimal point of the number, so it is usually not included when determining the number of significant figures. The mantissa has as many significant figures as the number whose log was found. So in the above examples:
- Example 1: log 5.43 x 1010 = 10.735
The number has 3 significant figures, but its log ends up with 5 significant figures, since the mantissa has 3 and the characteristic has 2. - Example 2: log 2.7 x 10-8 = -7.57
The number has 2 significant figures, but its log ends up with 3 significant figures.
Natural logarithms work in the same way:
- Example 3: ln 3.95 x 106 = 15.18922614... = 15.189
Application to pH problems:
pH = -log (hydrogen ion concentration) = -log [H+]
- Example 4: What is the pH of an aqueous solution when the concentration of hydrogen ion is 5.0 x 10-4 M?
pH = -log [H+] = -log (5.0 x 10-4) = - (-3.30) = 3.30
FINDING ANTILOGARITHMS (also called Inverse Logarithm)
Sometimes we know the logarithm (or ln) of a number and must work backwards to find the number itself. This is called finding the antilogarithm or inverse logarithm of the number. To do this using most simple scientific calculators,
- enter the number,
- press the inverse (inv) or shift button, then
- press the log (or ln) button. It might also be labeled the 10x (or ex) button.
- Example 5: log x = 4.203; so, x = inverse log of 4.203 = 15958.79147..... (too many significant figures)
There are three significant figures in the mantissa of the log, so the number has 3 significant figures. The answer to the correct number of significant figures is 1.60 x 104. - Example 6: log x = -15.3;
so, x = inv log (-15.3) = 5.011872336... x 10-16 = 5 x 10-16 (1 significant figure)
Natural logarithms work in the same way:
- Example 7: ln x = 2.56; so, x = inv ln (2.56) = 12.93581732... = 13 (2 sig. fig.)
Application to pH problems:
pH = -log (hydrogen ion concentration) = -log [H+]
- Example 8: What is the concentration of the hydrogen ion concentration in an aqueous solution with pH = 13.22?
pH = -log [H+] = 13.22
log [H+] = -13.22
[H+] = inv log (-13.22)
[H+] = 6.0 x 10-14 M (2 sig. fig.)
CALCULATIONS INVOLVING LOGARITHMS
Because logarithms are exponents, mathematical operations involving them follow the same rules as those for exponents.
| Common Logarithm | Natural Logarithm |
|---|---|
| log xy = log x + log y | ln xy = ln x + ln y |
| log x/y = log x - log y | ln x/y = ln x - ln y |
| log xy = y log x | ln xy = y ln x |
log 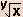 = log x1/y = (1/y )log x = log x1/y = (1/y )log x |
ln 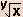 = ln x1/y =(1/y)ln x = ln x1/y =(1/y)ln x |
- Example 9: log 5.0 x 106 = log 5.0 + log 106 = 0.70 + 6 = 6.70
Hint: This is an easy way to estimate the log of a number in scientific notation! - Example 10: log (154/25) = log 154 - log 25 = 2.188 - 1.40 = 0.788 = 0.79 (2 sig. fig.)
- Example 11: log (5.46 x 10-3)6 = 6 log 5.46 x 10-3 = 6 x (-2.263) = -13.58
- Example 12: log (4.35)1/4 = 1/4 log 4.35 = 0.160
QUIZ: Give the correct answer to the correct number of significant figures.
| Question 1 | log 23.0 = ? |
| Question 2 | What is the pH of an aqueous solution in which [H+] = 2.7 x 10-3 M? |
| Question 3 | Find x if log x = 10.23. |
| Question 4 | If the pH of an aqueous solution is 6.52, what is the concentration of the hydrogen ion? |
| Question 5 | log (1.2 x 106)3 = ? |
Answers: (1) 1.362 (2) 2.57 (3) 1.7 x 1010 (4) 3.0 x 10-7 M (5) 18.24

LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.

Full Live Access

Study Material

Live Doubts Solving

Daily Class Assignments
Other Related Questions on discuss with colleagues and iitians

Are core branches(Mechanical) in Top 3 NIT worth it ?
discuss with colleagues and iitians
Last Activity: 3 Years ago

My rank in JEE Advanced 2022 is 1871. Should I go for IIT Guwahati ECE or IIT Kanpur Mechanical and try for a branch change to CS or Electrical Engineering? Is changing your branch very difficult?
discuss with colleagues and iitians
Last Activity: 3 Years ago

Can i sacrifice board exams for jee mains as board exams are no where valueable as cuet and other will be seen for admission
discuss with colleagues and iitians
Last Activity: 3 Years ago

Is a student studying in IGCSE syllabus eligible for taking IOQP or IOQJS?
discuss with colleagues and iitians
Last Activity: 3 Years ago

I have wasted my 11th? Is it still possible to get into my dream iit? Do i have to cover 11 th syllabus first? When and how can i finish it?
discuss with colleagues and iitians
Last Activity: 3 Years ago

