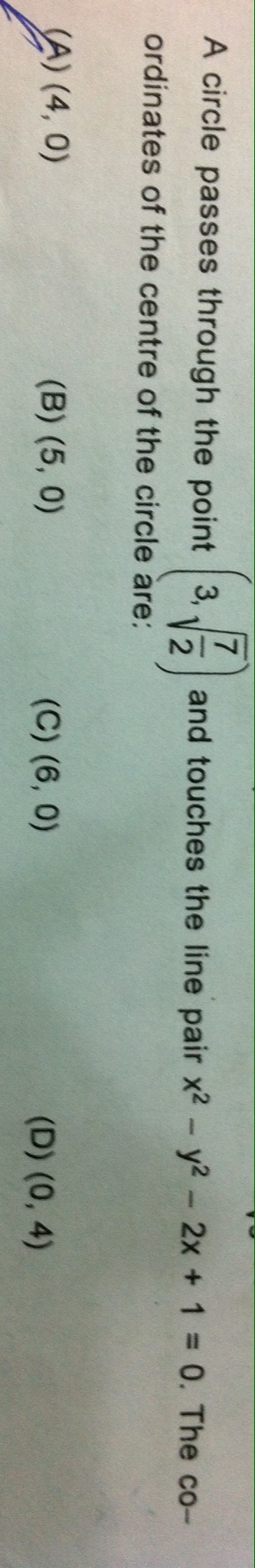0

Guest

Courses New

A circle passes through the point (3,(7/2)^0.5) and touches the line pair x^2 – y^2 -2x+1=0. the co ordinates of centre of circle are? (4,0) (6,0)

 
A circle passes through the point (3,(7/2)^0.5) and touches the line pair x^2 – y^2 -2x+1=0. the co ordinates of centre of circle are?
  1. (4,0)
    1. (6,0)

Question Image
Grade:11

1 Answers

Riddhish Bhalodia
askIITians Faculty 434 Points
8 years ago
OK
so first we solve for the lines
x^2-y^2 -2x+1 = (x-1)^2 - y^2 = 0
whihc gives the two lines as
x+y=1 \quad and \quad x-y=1
and now plotting them on the coordinate axes, it’s easy to see by symmetry that the center of circle would lie on x- axis and hence will be of the form
(a,0).
thus we can equate the radius
perpendicular distance from (a,0) to the line x+y=1 is equal to the distance between points (a,0) \quad and \quad (3,\sqrt{7/2})

thus the equation will be
|a-1|/\sqrt{2} = \sqrt{(a-3)^2 + 7/2}
solving the quadratic we get a as
a=4 and a=6
so the answer is A and C

Think You Can Provide A Better Answer ?

Other Related Questions on Analytical Geometry

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More