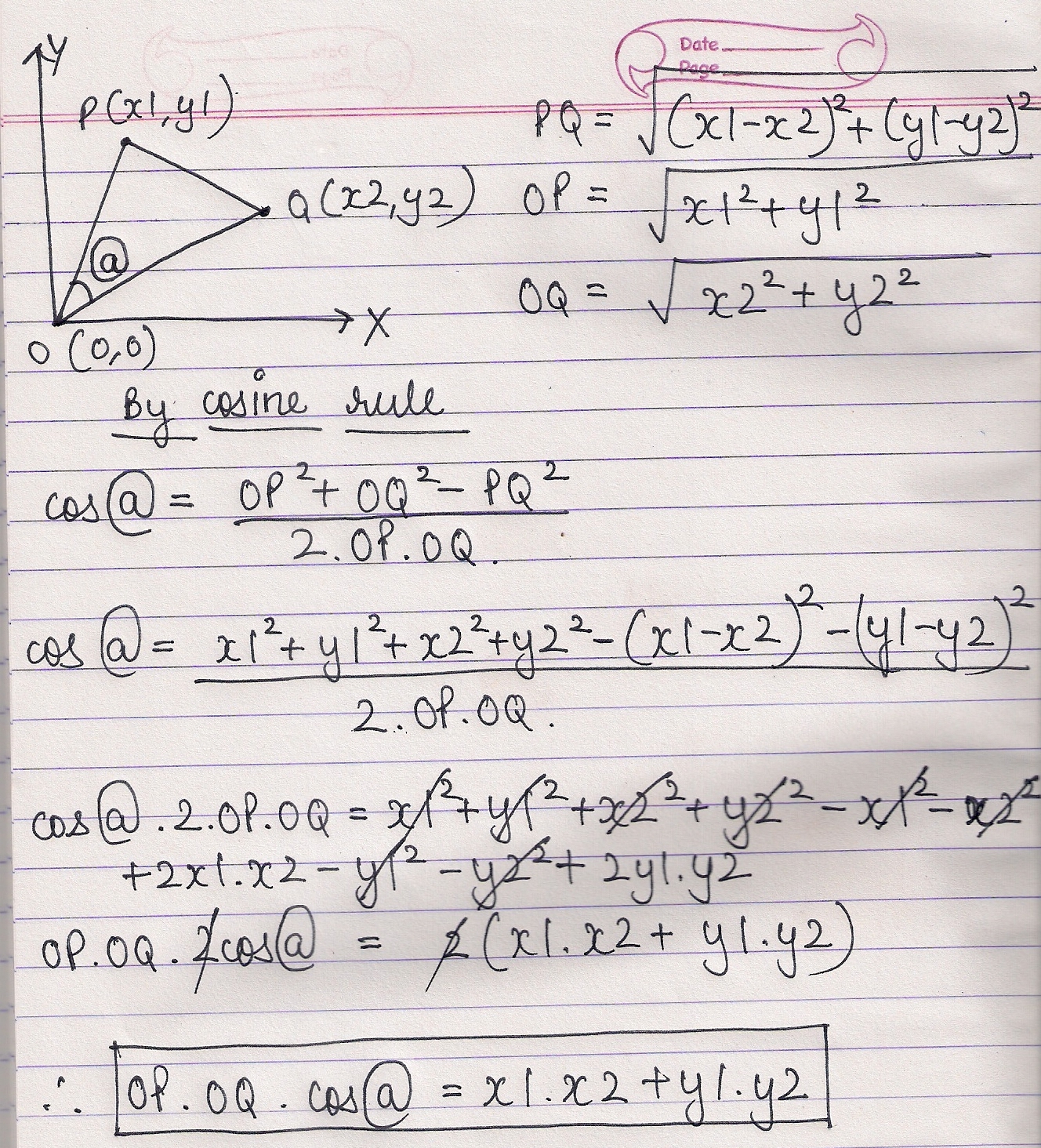Click to Chat
1800-2000-838
+91-120-4616500
CART 0
Use Coupon: CART20 and get 20% off on all online Study Material
Welcome User
OR
LOGIN
Complete Your Registration (Step 2 of 2 )
If the line segment joining the points P(x1,y1) and Q(x2,y2) subtends an qngle @ at origin O prove that OP.OQcos@ = x1x2 +y1y2
If the line segment joining the points P(x1,y1) and Q(x2,y2) subtends an qngle @ at origin O
prove that OP.OQcos@ = x1x2 +y1y2
hey yar op.oqcos@=>x1.x2cos0+x1.y1cos90+x2.y1cos90+x1.y2cos90+x2.y2cos90+y1.y2cos0 since (x1 and x2) and (y1 and y2)are in straight line
hey yar
op.oqcos@=>x1.x2cos0+x1.y1cos90+x2.y1cos90+x1.y2cos90+x2.y2cos90+y1.y2cos0
since (x1 and x2) and (y1 and y2)are in straight line
hey yar by resolution of vectors op.oqcos@=>x1.x2cos0+x1.y1cos90+x2.y1cos90+x1.y2cos90+x2.y2cos90+y1.y2cos0 since (x1 and x2) and (y1 and y2)are in straight line therefore the answer becomes OP.OQcos@=x1x2+y1y2 since cos0=1 and cos 90=0 thus prooved
by resolution of vectors
therefore the answer becomes
OP.OQcos@=x1x2+y1y2
since cos0=1 and cos 90=0
thus prooved
As the line OP and OQ subtends an angle @, so we can use cosine law........... 2.OP.OQ.cos@ =(X1^2+Y1^2)+(X2^2+Y2^2)- {(X1-X2)^2+(Y1-Y2)^} =2X1X2+2Y1Y2 SO OP.OQ.COS@= X1X2 + Y1Y2
As the line OP and OQ subtends an angle @, so we can use cosine law...........
2.OP.OQ.cos@ =(X1^2+Y1^2)+(X2^2+Y2^2)- {(X1-X2)^2+(Y1-Y2)^}
=2X1X2+2Y1Y2
SO OP.OQ.COS@= X1X2 + Y1Y2
Post Question
Dear , Preparing for entrance exams? Register yourself for the free demo class from askiitians.
points won -