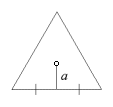
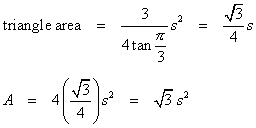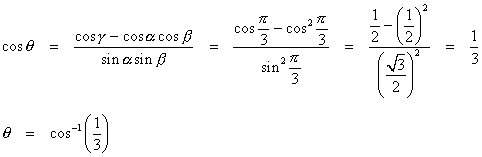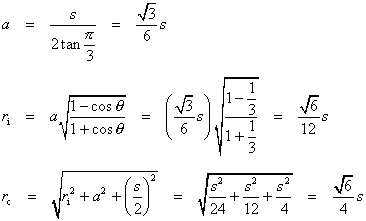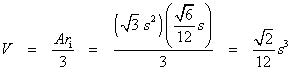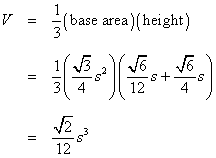Ask a Doubt
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on analytical geometry

The locus of the point represented by x= t^2 +t+1 and y=t^-t+1 is
analytical geometry
0 Answer Available
Last Activity: 2 Years ago

show that the centroids of the triangles of which three perpendiculars lie along the lines y=m1x,y=m2x,y=m3x lie on y(3+m2m3+m3m2+m1m2)=x(m1+m2+m3+3m1m2m3)
analytical geometry
0 Answer Available
Last Activity: 2 Years ago

show that the equation (ab-h²)(ax²+2hxy+by²+2gx+2fy)+af²+bg²-2fgh=0 represent a pair of straight lines and that these straight lines form a rhombus with the lines ax²+2hxy+by²=0
analytical geometry
0 Answer Available
Last Activity: 2 Years ago

A circle has its center on straight line 5x-2y+1=0 and cuts the x axis at two points whose absciasse are -5,3 find equation of the circle and it's radius.
analytical geometry
0 Answer Available
Last Activity: 2 Years ago

Prove that ax^2+by^2+cz^2 +2ux+2vy+2wz+d=0 represent a cone if u^2/a+v^/b+w^2/c=d
analytical geometry
0 Answer Available
Last Activity: 2 Years ago