Samyak Jain
Last Activity: 5 Years ago
Ans. is 8.
We know that formula of variance is [∑(x
i –
)
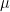
2 ] / N, where i = 1,2, …, N ,
x
i are observations,
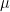
is mean, N is number of observations.
Solving this we get variance = [∑x
i2 – N
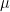2] / N = (∑x
i2 / N) –
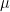2 and standard deviation is square root of variance.
Initial mean (
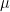1) = 25 = ∑x
i / 8
Initial standard deviation (
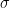
) = 5
Initial variance (
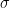2) = 5
2 = 25 = (∑x
i2 / 8) –
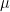12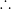 
25 = (∑x
i2 / 8) – 25
2 or (∑x
i2 / 8) = 25 + 625 = 650
∑xi2 = 650 x 8 = 5200.
Now, finally there are 10 items.
Final mean,
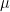2 = (
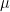1 x 8 + 15 + 25) / 10 = (25 x 8 +15 + 25) / 10 = 240 / 10 =
24.
Final variance = (final ∑x
i2 / final N) –
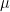2 2 = {(5200 + 15
2 + 25
2) / 10} – 24
2 = {(5200 + 225 + 625) / 10} – 576
= 605 – 576
= 29.
