proof of L'hospitals theorem

Dear sachin,

If f and g are differentiable in a neighborhood of x = c, and f(c) = g(c) = 0, then

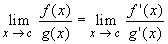
provided the limit on the right exists. The same result holds for one-sided limits.

If f and g are differentiable and 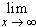f(x) = 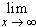g(x) = - 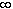then

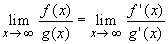
provided the last limit exists.

Proof:

The first part can be proved easily, if the right hand limit equals f'(c) / g'(c): Since f(c) = g(c) = 0 we have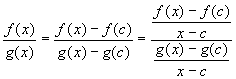

Taking the limit as x approaches c we get the first result. However, the actual result is somewhat more general, and we have to be slightly more careful. We will use a version of the Mean Value theorem:

Take any sequence {x_n} converging to c from above. All assumptions of the generalized Mean Value theorem are satisfied (check !) on [c, x_n]. Therefore, for each n there exists a number c_n in the interval (c, x_n) such that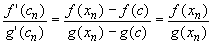

We are all IITians and here to help you in your IIT JEE preparation.

All the best.

 If you like this answer please approve it....

win exciting gifts by answering the questions on Discussion Forum

Consider the linear approximation to f(x) and g(x) at x=a:

The ratio of these for x near a is:

which, if g'(a) is not 0 approaches f '(a) / g'(a) as x approaches a.

If g'(a) = 0 and f '(a) = 0 we can apply the same rule to the derivatives, to give f "(a) / g"(a).

If these second derivatives are both 0 you can continue to higher derivatives, etc. the result will be the ratio of the first pair of non-vanishing higher derivatives at a.

Of course if the first non-vanishing derivative of the numerator is the kth and occurs before the kth then the ratio is 0; if the first non-vanishing entry of the denominator occurs after that of the numerator, the ratio goes to infinity at a.