Revision Notes on Ellipse

• The standard equation of ellipse with reference to its principal axis along the coordinate axis is given by x2/a2 + y2/b2 = 1
• In the standard equation, a >b and b2 = a2 (1-e2) Hence, the relation between a and b is a2 – b2 = a2e2, where ‘e’ is the eccentricity and 0 < e < 1.

• The foci of the ellipse are S(ae, 0) and S’ = (-ae, 0)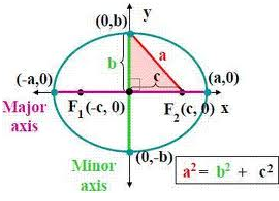

• Equations of the directrices are given by x = a/e and x = -a/e

• The coordinates of vertices are A’ = (-a, 0) and A = (a,0)

• The lengths of the major and minor axis are 2a and 2b respectively.

• The length of latus rectum is 2b2/a = 2a(1-e2)

• The sum of the focal distances of any pint on the ellipse is equal to the major axis. As a result, the distance of focus from the extremity of a minor axis is equal to semi major axis.

• If a question does not mention the relation between a and b then by convention a is assumed to be greater than b i.e. a > b.

• The point P(x1, y1) lies outside, inside or on the ellipse according as x12/a2 + y12/b2 – 1>< or = 0.

• In parametric form, the equations x = a cos θ and y = b sin θ together represent the ellipse.

• The line y = mx + c meets the ellipse x2/a2 + y2/b2 = 1 in either two real, coincident or imaginary points according to whether c2 is < = or > a2m2 + b2

• The equation y = mx + c is a tangent to the ellipse if c2 = a2m2+ b2

• The equation of the chord of ellipse that joins two points with eccentric angles α and β is given byx/acos (α + β)/2 + y/b sin (α + β)/2 = cos (α - β)/2

• The equation of tangent to the ellipse at the point (x1, y1) is given byxx1/a2 + yy1/b2 = 1

• In parametric form, (xcosθ) /a + (ysinθ/b) is the tangent to the ellipse at the point (a cos θ a, b sin θ)

• Equation of normal

1. Equation of normal at the point (x₁,y₁) is

a2x/x1 – b2y/y1 = a2- b2 = a2e2

2. Equation of normal at the point (a cos θ a, b sin θ) is ax secθ – by cosec θ = (a2-b2)

3. Equation of normal in terms of its slope ‘m’ is

y = mx – [(a2-b2)m /√a2+b2m2]

• The equation of director circle is x2+ y2= a2 + b2  

• The portion of the tangent to an ellipse between the point of contact and the directrix subtends a right angle at the corresponding focus.

The perpendiculars from the center upon all chords which join the ends of any particular diameters of the ellipse are of constant length.