Light Reflection and Refraction CBSE Class 10 Science Revision Notes Chapter 10

 

Laws of Reflection

• The angle of incidence is equal to angle of reflection

• Incident ray, reflected ray and normal all lie in the same plane.

Spherical Mirrors

Most common type of curved mirrors are spherical mirrors. Mirrors in which reflecting surface are spherical in shape, is known as spherical mirrors. Reflecting surface of a mirror can be curved inwards or curved outwards. The one which is curved inward is known as concave mirror and the one which curved outwards is known as convex mirror.

Fig.1. Spherical mirrors

Some Important Terms

• Pole- The centre of the reflecting surface in a spherical mirror is a pole. It is represented by P.

• Centre of curvature- Reflecting surface in a spherical mirror has a centre, this is known as centre of curvature. Centre of curvature in convex mirror lies behind the mirror whereas in concave mirror, it lies in front of the mirror.

• Radius of curvature- The radius of the reflecting surface of the spherical mirror is known as radius of curvature. It is represented by R.

• Principal axis- Straight line passing through the pole and centre of curvature in a spherical mirror is known as principal axis.

• Principal focus- The reflected rays appear to come from a point on the principal axis, this is known as principal focus.

• Focal length- The distance between the pole and the principal focus in a spherical mirror is known as focal length and it is represented by f.

• Aperture- The diameter of the reflecting surface is defined as aperture.

Note: Radius of curvature is twice the focal length (R=2f).

Fig.2. Image showing pole, principal axis, centre of curvature, aperture and principal focus in concave mirror

Representations of the images formed by Spherical Mirrors using Ray Diagrams

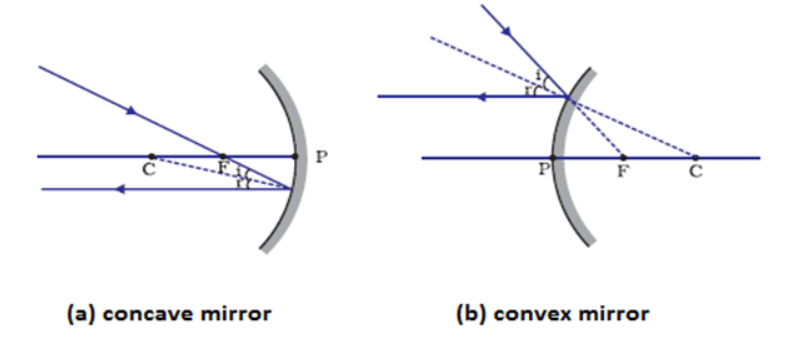
We draw the ray diagram to locate the image of an object formed. The intersection point of at least two reflected will give the position of image of the point object. The two rays that can be used to draw the ray diagram are-

• A ray parallel to the principal axis should pass through the focus after reflection in case of concave mirror, or appear to diverge in case of convex mirror.

• A ray passing through the focus of the concave mirror or directed towards the focus in case of convex mirror, should appear parallel to the principal axis after reflection.

• A ray which is passing through the centre of curvature in a concave mirror or directed in case of convex mirror, should reflect along the same path.

• A ray when incident obliquely to principal axis on a concave or convex mirror is also reflected obliquely.

Image formation by Concave Mirror

Fig. 3.  Ray diagram for the image formation by concave mirror

Position of the object	Position of the image	Size of the image	Nature of the image
At infinity	At the focus F	Highly diminished	Real and inverted
Beyond C	Between F and C	Diminished	Real and inverted
At C	At C	Same size	Real and inverted
Between C and F	Beyond C	Enlarged	Real and inverted
At F	At infinity	Highly enlarged	Real and inverted
Between P and F	Behind the mirror	Enlarged	Virtual and erect

Table.1.  Nature, relative size and position of the image formed by concave mirror

Position, nature, and the size of the image formed by a concave mirror is dependent on the position of the object in relation to P, C and F. Image formed can be real or virtual. The image can also be magnified, diminished or even of the same size.

Uses of Concave Mirror

Used in search lights, torches, head lights of the vehicles. Also used in shaving mirrors. Used by dentists also to see larger image of the teeth. Other use in solar furnaces.

Image formation by Convex Mirror

Two positions of the object are considered while understanding the image formed by convex mirror. Either the object should be at infinity or at finite distance from the mirror. Formation of the image by the convex mirror are as follows-

Fig. 5. Ray diagram for the image formation by convex mirror

Position of the object	Position of the image	Size of the image	Nature of the image
At infinity	At the focus F, behind the mirror	Highly diminished	Virtual and erect
Between infinity and the pole P of the mirror	Between P and F, behind the mirror	Diminished	Virtual and erect

Table.2.  Nature, relative size and position of the image formed by convex mirror

Uses of Convex Mirror

They are used as rear-view mirrors. They are used to see the traffic behind. They are preferred as they give erect but diminished image.

Sign convention for reflection by spherical mirrors

New cartesian sign convention is used to give sign convention used for spherical mirrors. The conventions are as follows-

1. The object is always placed to the left of the mirror.

2. All distances parallel to the principal axis are measured from the pole of the mirror.

3. All the distances measured to the right of the origin (along + x-axis) are taken as positive while those measured to the left of the origin (along – x-axis) are taken as negative.

4. Distances measured perpendicular to and above the principal axis (along + y-axis) will be taken as positive.

5. Distances measured perpendicular to and below the principal axis (along –y-axis) will be taken as negative.

Mirror formula and magnification

The distance of the object from its pole is known as object distance (u), whereas distance from the pole of the mirror is known as image distance (v). The mirror formula is given by-

It is applicable for spherical mirrors in all positions of the object.

Magnification

It is defined as relative extent to which an object is magnified in comparison to its object size.

Where m is the magnification, h_o is the height of the object and h_i is the height of the image. However, it is to be taken as negative for real images. A negative sign in the value of magnification indicates that the nature of the image is real. A positive sign in the value of the magnification indicates the virtual nature of the image.

Refraction of light

Bending of the light rays as it passes from one medium to another medium is known as refraction of light.

Laws of Refraction

• Incident ray, refracted ray and normal all lie in the same plane.

• The ratio of sine of angle of incidence to the sine of angle of refraction is constant. This law is also known as Snell’s law of refraction. 

Refractive Index

When light passes from one medium to another medium, it changes its direction. The extent to which the direction changes is expressed in terms of refractive index. The value of refractive index is dependent on the speed of light in two media. v₁ is the speed of light in medium 1 and v₂ is the speed of light in medium 2. The refractive index of medium 2 with respect to medium 1 is represented as n₂₁.

If medium 1 is vacuum or air, then the refractive index of medium 2 with respect to vacuum is known as absolute refractive index of the medium.

Where c is the speed of light in air, v is the speed of light in other medium and n_m is the refractive index of the medium.

Refraction by Spherical Lenses

Lenses are defined as transparent materials which are bounded by two surfaces, out of which one or both can be spherical. When both the two spherical surfaces bulge outwards, it is known as convex lens. They converge the light rays. When the two spherical surfaces bulge inwards, they are known as concave lens. They are known as diverging lens. The centre of these spherical surfaces is known as centre of curvature, represented by C.

Any imaginary straight line passing through the centre of curvature of a lens is known as principal axis. The centre point is known as optical centre. The effective diameter of the spherical lens is known as aperture.

Image formation by lenses

Nature, relative size, and position of the image formed by convex lens are given below in the form of table-

Position of the object	Position of the image	Relative size of the image	Nature of the image
At infinity	At focus F2	Highly diminished	Real and inverted
Beyond 2F1	Between F2 and 2F2	Diminished	Real and inverted
At 2F1	At 2F2	Same size	Real and inverted
Between F1 and 2F1	Beyond 2F2	Enlarged	Real and inverted
At focus F1	At infinity	Infinitely large	Real and inverted
Between focus F1 and optical centre O	On the same side of the lens as the object	Enlarged	Virtual and erect

Image formation in Lenses using Ray Diagrams

Rules for drawing the ray diagrams are as follows-

1. A ray of light which is parallel to the principal axis will pass through the principal focus after refraction from the convex lens.

2. A ray of light passing through principal focus, will emerge parallel to principal axis after refraction from the convex lens.

3. A light ray passing through optical centre will emerge out without any deviation.

Image formed by the Convex Lens for various positions of the object

Image formed by the Concave Lens

Sign convention for Spherical Lenses

Sign convention are used as similar for spherical mirrors. But the focal length of a convex lens is positive and that of concave lens in negative.

Lens formula and magnification

The lens formula is given as

Where, u is object distance, v is image distance and f is focal length.

The ratio of the height of an image to the height of an object is defined as magnification.

Magnification is represented by m, h₀ is the height of the object and h_i is the height of the image.

Power of a Lens

The degree of convergence or divergence of light rays is expressed in terms of power. So, the reciprocal of focal length is known as its power. It is represented by letter P. The power is given by-

P = 1/f

The SI unit of power is dioptre. It is represented by D. Power of concave lens is negative and power of convex lens is positive.

 

You Might Like to Refer:

Neet coaching |CBSE Online Class 10 | cbse study material for class 12