Revision Notes on Quadratic Equations

• Remainder Theorem:

It states that if a polynomial P(x) is divided by a linear function (x – k), then the remainder is P(k).

P(x)/(x – k) = Q(x) + R/(x – k), where Q(x) is quotient and R is remainder.

So, P(x) = Q(x)(x-k) + R at x = k, P(k) = R.

• Factor theorem:

Let P(x) = (x – k)Q(x) + R

when P(k) = 0, P(x) = (x – k)Q(x). Therefore, P(x) is eaxctly divisible by (x – k).

• In order to solve a quadratic equation of the form ax² + bx + c, we first need to calculate the discriminant with the help of the formula D = b² – 4ac.

• The solution of the quadratic equation ax² + bx + c = 0 is given by x = [- b ± √ b² – 4ac] / 2a

• If α and β are the roots of the quadratic equation ax² + bx + c = 0, then we have the following results for the sum and product of roots:

       α + β = -b/a

       α.β = c/a

       α – β = √D/a

• It is not possible for a quadratic equation to have three different roots and if in any case it happens, then the equation becomes an identity.

• Nature of Roots:

Consider an equation ax² + bx + c = 0, where a, b and c ∈ R and a ≠ 0, then we have the following cases:

(a) D > 0 iff the roots are real and distinct i.e. the roots are unequal

(b) D = 0 iff the roots are real and coincident i.e. equal

(c) D < 0 iff the roots are imaginary

(d) The imaginary roots always occur in pairs i.e. if a + ib is one root of a quadratic equation, then the other root must be the conjugate i.e. a-ib, where a, b ∈ R and i = √-1.

Consider an equation ax² + bx + c = 0, where a, b and c ∈ Q and a ≠ 0, then

(a) If D > 0 and is also a perfect square then the roots are rational and unequal.

(b) If α = p + √q is a root of the equation, where ‘p’ is rational and √q is a surd, then the other root must be the conjugate of it i.e. β = p - √q and vice versa.

• Roots under partciular cases:

(a) Exactly one root is at infinity:

If exactly one root is ∞ and the other root is finite, then co-efficient of x² must tend to zero and coefficient of x must not be equal to zero. 

(b) Both the roots at infinity:

When both roots of the equation are infinity, then the co-efficient of x² and co-efficient of x both must tend to zero and c must not be equal to zero.  

• Quadratic Equation and its graph:

The most general form of quadratic equation is ax² + bx + c, where a is non-zero. We now discuss different shapes of graphs obtained corresponding to different values of a, b and c.

Case 1: If a > 0 and D > 0

Then the quadratic equation has two roots and the graph cuts the x-axis at two different points.

Case 2: If a > 0 and D = 0

Then the curve touches the x-axis and hence both the zeroes of polynomial coincide.

Case 3: If a > 0 and D < 0

Then the curve lies completely above the x-axis.

Case 4: If a < 0 and D > 0

Then the graph is downward and the curve cuts the x-axis at two distinct points.

Case 5: If a < 0 and D = 0

Then the graph touches the x-axis from below.

Case 6: If a < 0 and D < 0

Then the graph lies completely below the x-axis and y < 0 for x ∈ R.

The following figure clearly illustrates the position of the graph in these cases:

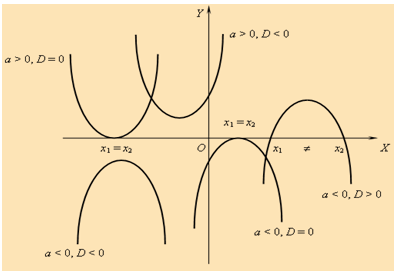
• If the roots of the quadratic equation are known, then the quadratic equation may be constructed with the help of the formula

    x² – (Sum of roots)x + (Product of roots) = 0.

   So if α and β are the roots of equation then the quadratic equation is

   x² – (α + β)x + α β = 0

• For the quadratic expressiony = ax² + bx + c, where a, b, c ∈ R and a ≠ 0, then the graph between x and y is always a parabola.

(a) If a > 0, then the shape of the parabola is concave upwards

(b) If a < 0, then the shape of the parabola is concave upwards

• Inequalities of the form P(x)/ Q(x) > 0 can be easily solved by the method of intervals of number line rule.

• Solving quadratic and rational inequalities (Wavy Curve Method):

While solving such inequalities, the following steps should be taken

(a) Factorize the given expression into linear factors.

(b) Make the coefficient of x positive in all the factors.

(c) Plot the points where given expression vanishes or becomes undefined on number line in increasing order.

(d) Start the number line from right to left taking positive or negative value.

• The maximum and minimum values of the expression y = ax² + bx + c occur at the point x = -b/2a depending on whether a > 0 or a < 0.

(a) y ∈ [(4ac-b²) / 4a, ∞] if a > 0

(b) If a < 0, then y ∈ [-∞, (4ac-b²) / 4a]

• The quadratic function of the form f(x, y) = ax²+by² + 2hxy + 2gx + 2fy + c = 0 can be resolved into two linear factors provided it satisfies the following condition: abc + 2fgh –af² – bg² – ch² = 0

• In general, if α₁,α₂, α₃, …… ,α_n are the roots of the equation

f(x) = a₀xⁿ +a₁x^n-1 + a₂x^n-2 + ……. + a_n-1x + a_n, then

(a) Σ α₁ = - a₁/a₀

(b) Σ α₁α₂ = a₂/a₀

(c) Σ α₁α₂α₃ = - a₃/a₀

………   ……….

Σ α₁α₂α₃ ……α_n= (-1)ⁿ a_n/a₀

• Every equation of n^th degree has exactly n roots (n ≥1) and if it has more than n roots then the equation becomes an identity.

• If there are two real numbers ‘a’ and ‘b’ such that f(a) and f(b) are of opposite signs, then f(x) = 0 must have at least one real root between ‘a’ and ‘b’.

• Every equation f(x) = 0 of odd degree has at least one real root of a sign opposite to that of its last term.

• Condition for a common root:

(a) Let a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0 have a common root α then the required condition is given by:

α = (b₁c₂ - b₂c₁)/ (a₂c₁ - a₁c₂) = (a₂c₁ - a₁c₂)/(a₁b₂ - a₂b₁)

(b) If both the roots of the given equation are common then a₁/a₂ =  b₁/b₂  = c₁/c₂.

• Log inequalities:

(a) For a > 1, if log_ax > log_ay, then this gives x > y that is if base is greater than unity the inequality remains unchanged when log is removed.

(b) For 0 < a < 1, if log_ax > log_ay, then this gives x < y that is if base is less than unity the inequality sign is reversed when log is removed.

(c) If a > 1, log_ax < P then x < a^P.

(d) If a > 1, log_ax > P then x > a^P.

(e) If a < 1, log_ax < P then x > a^P.

(f) If a < 1, log_ax > P then x < a^P.

• To solve log inequality when base is constant:

First of all find that the base is positive, expression inside the log is positive and the base is not equal to unity. Thios is known as the initial condition

Check whether the base is greater than unity or less than unity.

If base is greater than unity then remove the log without changing the inequality and if the base is less than unity then reverse the inequality when log is removed.

Solve the inequality and term it as the final condition.

Take the inetrsection of the intial and final condition.

• To solve log inequality when base is variable:

(a) Define log i.e. find that the base is positive, expression inside the log is positive and the base is not equal to unity. Thios is known as the initial condition.

(b) Take the case I where base is greater than unity and call it condition I.

(c) Solve the inequality as per case I i.e. remove the log without changing the inequality label it as condition I(s).

(d) Take the intersection of condition I, I(s) and initial condition and term it as condition L.

(e) Take the case 2, when base is less than unity and term it as condition 2.

(f) Solve the inequality as per case 2 i.e. reverse the inequality on removing the log and term it as condition 2(s).

(g) Take the intersection of condition 2, 2(s) and initial condition and term it as condition T.

(h) Take the union of conditions S and T.