Revision Notes on Ellipse

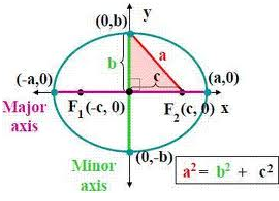
• The standard equation of ellipse with reference to its principal axis along the coordinate axis is given by x²/a² + y²/b² = 1

• In the standard equation, a > b and b² = a² (1 – e²) Hence, the relation between a and b is a² – b² = a²e², where ‘e’ is the eccentricity and 0 < e < 1.

• The foci of the ellipse are S(ae, 0) and S’ = (-ae, 0)

• Equations of the directrices are given by x = a/e and x = -a/e

• The coordinates of vertices are A’ = (-a, 0) and A = (a,0)

• The lengths of the major and minor axis are 2a and 2b respectively.

• The length of latus rectum is 2b²/a = 2a(1 - e²)

• Distance between the two foci is 2ae and distance between directrix is 2a/e.

• Two ellipses are said to be similar if they have the same eccentricity.

• The sum of the focal distances of any pint on the ellipse is equal to the major axis. As a result, the distance of focus from the extremity of a minor axis is equal to semi major axis.

• The circle described on the major axis of an ellipse as diameter is called the auxiliary circle.

• If a question does not mention the relation between a and b then by convention a is assumed to be greater than b i.e. a > b.

• The point P(x₁, y₁) lies outside, inside or on the ellipse according as x₁²/a² + y₁²/b² – 1 >, < or = 0.

• In parametric form, the equations x = a cos θ and y = b sin θ together represent the ellipse.

• Comparison Chart between Standard Ellipse:?

Basic Elements	x2/a2 + y2/b2 = 1
	a > b	a < b
centre	(0, 0)	(0, 0)
vertex	(±a, 0)	(0, ±b)
Length of major axis	2a	2b
Length of minor axis	2b	2a
foci	(± ae, 0)	(0, ± be)
Equation of directirx	x = ± a/e	y = ± b/e
Relation between a, b and c	b2 = a2(1 – e2)	a2 = b2(1 – e2)
Equation of major axis	y = 0	x = 0
Equation of minor axis	x = 0	y = 0
Length of latus rectum	2b2/a	2a2/b
Ends of latus rectum	(± ae, ± b2/a)	(± a2/b, ± be)
Distance between foci	2ae	2be
Distance between directrix	2a/e	2b/e
Parametric equation	(a cos θ, b sin θ) (0 < θ < 2π)	(a cos θ, b sin θ)

• The line y = mx + c meets the ellipse x²/a² + y²/b² = 1 in either two real, coincident or imaginary points according to whether c² is < = or > a²m² + b²

• The equation y = mx + c is a tangent to the ellipse if c² = a²m² + b²

• The equation of the chord of ellipse that joins two points with eccentric angles α and β is given by
  x/a cos (α + β)/2 + y/b sin (α + β)/2 = cos (α - β)/2

• Equation of tangent to the ellipse:

• The equation of tangent to the ellipse at the point (x₁, y₁) is given by xx₁/a² + yy₁/b² = 1

• In parametric form, (x cos θ) /a + (y sin θ) /b = 1 is the tangent to the ellipse at the point (a cos θ, b sin θ).

• Equation of normal:

• Equation of normal at the point (x₁,y₁) is a²x/x₁ – b²y/y₁ = a² - b² = a²e²

• Equation of normal at the point (a cos θ a, b sin θ) is ax sec θ – by cosec θ = (a² - b²)

• Equation of normal in terms of its slope ‘m’ is y = mx – [(a² - b²)m /√a² + b²m²]

• The equation of director circle is x² + y² = a² + b²  

• Chord of contact:

Pair of tangents drawn form outside point P(x₁, y₁) to the ellipse meet it at R and P. Line joining P and R is called the chord of contact of point P(x₁, y1) with respect to the ellipse. The equation of chord of contact is 

xx₁/a² + yy₁/b² = 1.

• The portion of the tangent to an ellipse between the point of contact and the directrix subtends a right angle at the corresponding focus.

• The perpendiculars from the center upon all chords which join the ends of any particular diameters of the ellipse are of constant length.

• Chord with a given middle point:

AB is a chord of the circle whose mid-point is P(x₁, y₁). Then the equation of the chord AB is T = S₁, where

S₁ = x₁²/a² + y₁²/b² – 1 and T = xx₁/a² + yy₁/b² – 1.

• Two diameters of ellipse are said to be conjugate diameters if each bisects the chords parallel to the other.

• The eccentric angles at the ends of a pair of conjugate diameters of an ellipse differ by a right angle.

• The sum of squares of any two conjugate semi-diameters of an ellipse is constant and equal to the sum of squares of semi-axis of ellipse.