Chapter 3: Functions – Exercise 3.1

Functions – Exercise 3.1 – Q.1

Function = Let A and B be two non-empty sets. A relation f from A to B i.e. a sub-set of A × B, is called a function (or a mapping or a map) from A to B, if

(i) for each a ϵ A there exists b ϵ B such that (a, b) ϵ f

(ii) (a, b) ϵ f and (a, c) ϵ f ⟹ b = c

If (a, b) ϵ f, then 'b' is called the image of 'a' under f

If a function f is expresed as the set of ordered pairs, the domain f is the set of all first components of members of f and the range of f is the set of second components of members of f.

Functions – Exercise 3.1 – Q.2

Function = Let A and B be two non-empty sets. Then a function ' f' from set A to set B is a rule or method or correspondence which associates elements of set A to elements of set b such that:

(i) all elements of set A are associated to element in set B.

(ii) an element of se A is associated to a unique element in set B.

In other words, a function ' f' from a set A to set B associates each element of set A to a unique element of set b.

Functions – Exercise 3.1 – Q3

Function is a type of relation. But in a function no two ordered pairs have the same first element. For eg: R₁ and R₂ are two relations.

Clearly, R₁ is a function, but R₂ is not a function because two ordered pairs (1, 2) and (1, 4) have the same first element. This means every function is a relation but every relation is not a function.

Functions – Exercise 3.1 – Q4

We have,

f(x) = x² - 2x - 3

Now,

f(-2) = (-2)² - 2 (-2) - 3

= 4 + 4 - 3

= 5

f(-1) = (-1)² - 2(-1) - 3

= 1 + 2 - 3

= 0

f(-0) = (-0)² - 2 × 0 - 3

= - 3

f(1) = (1)² -2 × 1 - 3

= 1 - 2 – 3

= – 4

f(2) = (2)² - 2 × 2 - 3

= 4 - 4 - 3

= - 3

(a) Rang (f) = {-4, -3, 0, 5}

(b) Clearly, pre-images of 6,-3 and 5 is ∅, {0, 2}, -2 respectively.

Functions – Exercise 3.1 – Q5

We have,

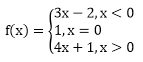
Now,

f(1) = 4 × 1 + 1 = 5,

f(-1) = 3 × (-1) - 2 = – 3 – 2 = – 5,

f(0) = 1,

 and, f(2) = 4 × 2 + 1 = 9

∴ f(1) = 5,   f(-1) = – 5,

f(0) = 1,   f(2) = 9,

Functions – Exercise 3.1 – Q6

We have,

f(x) = x²                      ---- (i)

(a) clearly range of f = R⁺ (set of all real numbers greater than or equal to zero)

(b) we have,

{x : f(x) = 4}

⟹ f(x) = 4            ---- (ii)

Using equation (i) and equation (ii), we get

x² = 4

⟹ x = ± 2

∴ {x : f(x) = 4} = {-2, 2}

(c) {y : f(y) = -1}

⟹ f(y) = -1 ---- (iii)

Clearly, x² ≠ -1 Or X² ≥ 0

⟹ f(y) ≠ –1

∴ {y : f(y) = –1} = ∅

Functions – Exercise 3.1 – Q7

We have,

f = R⁺ → R

and f(x) = log_e x     --- (i)

(a) Now

f = R⁺→ R

∴ the image set of the domain of f = R

(b) Now,

{x : f (x) = – 2}

⟹ f (x) = – 2            ----(ii)

Using equation (i) and equation (ii), we get

log_e x = – 2

⟹ x = e^-2

∴ {x : f (x) = – 2} = {e^-2}

(c) Now,

f(xy) = log_e (xy)                                 [f(x) = log_e x]

= log_e x + loge y                        [∵ logmn = logm + logn]

f(x) + f(y)

∴ f(xy) = f(x) + f(y)

Yes, f(xy) = f(x) + f(y).

Functions – Exercise 3.1 – Q8

(a) we have,

{(x, y) = y = 3x,x ϵ (1, 2, 3),y ϵ {3, 6, 9, 12}}

Putting x = 1,2, 3 in y = 3x, we get

y = 3, 6, 9 respectively

∴ R = {(1, 3), (2, 6), (3, 9)}

Yes, it is a function.

(b) we have,

{(x, y) : y > x + 1,x = 1, 2 and y = 2, 4, 6}

Putting x = 1, 2 in y > x + 1, we get y > 2, y > 3 respectively.

∴ R = {(1, 4), (1, 6), (2, 4), (2, 6)}

It is not a function from A to B because two ordered pairs in R have the same first element.

(c) we have,

{(x, y) = x + y = 3, x , y ϵ {0,1, 2, 3}}

Now,

y = 3 - x

Putting x = 0,1, 2, 3, we get

y = 3, 2, 1, 0 respectively

∴ R = {(0, 3), (1, 2), (2, 1,(3, 0)}

Yes, this relation is a function.

Functions – Exercise 3.1 – Q9

We have,

f : R → R and g : c → c

∴ Domain (f) = R and Domain (g) = c

∴ Domain (f) ≠ Domain (g) = c

∴ f(x) and g(x) are not equal functions.

Functions – Exercise 3.1 – Q10

(i) We have,

f(x) = x²

Range of f (x) = R⁺ (set of all real numbers greater than or equal to zero) = {x ϵ R|x ≥ 0}

(ii) We have,

g(x) = sinx

Range of g(x) = {x ϵ R : -1 x ≤ 1}

(iii) We have,

h(x) = x² + 1

Range of h (x) = {x ϵ P : ≥ 1}

Functions – Exercise 3.1 – Q11

(a) We have,

f₁ = {(1, 1), (2, 11), (3, 1), (4, 15)}

f₁ is a function from X to Y.

(b) We have,

f₂ = {(1, 1), (2, 7), (3, 5)}

f₂ is not a function from X to Y because there is an element 4 ϵ x which is not associated to any element of Y.

(c) We have,

f₃ = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}

f₃ is not a function from X to Y because an element 2 ϵ x is associated to two elements 9 and 11 in Y.