Chapter 8: Quadratic Equations Exercise – 8.1

Question: 1

Solve quadratic equations:

(i) x²  - 3x + 2 = 0 , x = 2 , x = - 1

(ii)  x² + x + 1 = 0, x = 0, x = 1

(v) 2x² - x + 9 = x² + 4x + 3, x = 2 and x = 3

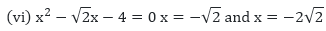
(vii) a²x² - 3abx + 2b² = 0

Solution:

(i) Here LHS = x² - 3x + 2 RHS = 0

Now, substitute x = 2 in LHS

We get, (2)² - 3(2) + 2

= 4 - 6 + 2

 = 6 - 6

= 0

RHS Since, LHS =RHS

Therefore, x - 2 is a solution of the given equation.

Similarly, substituting x = - 1 in

LHS

We get, (-1)² - 3(-1) + 2

 = 1 + 3 + 2

= 6

RHS Since, LHS?

RHS = x = - 1 is not the solution of the given equation.

(ii) Here,

LHS = x²  + x + 1 and RHS = 0

Now, substituting x = 0 and x = 1 in

LHS = 0² + 0 + 1

 = (1)² + 1 + 1

= 1 + 2

= 3 LHS

RHS Both x = 0 and x = 1 are not solutions of the given equation. 

(iii) Here,

LHS = x² - 3√3x + 6 = 0 and

RHS = 0 Substituting the value of x = √3 and x = - 2√3 in

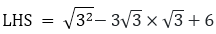
= 3 – 9 + 6

= 9 - 9

= 0

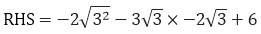
= 12 + 18 + 6

= 36

RHS x = √3 is a solution of the above mentioned equation. Whereas, x = - 2√3 is not a solution of the above mentioned equation. 
(iv) Here,

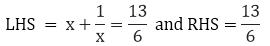
Substituting where x = 5/6 and x = 4/3 in the LHS

RHS where x = 5/6 and x = 4/3 are not the solutions of the given equation.

(v) 2x² - x + 9 = x² + 4x + 3, x = 2

= 2x² - x + 9 - x² + 4x + 3 = x² - 5x + 6 = 0

Here, LHS = x² - 5x + 6 and RHS = 0

Substituting x = 2 and x = 3

= x² - 5x + 6

= (2)² - 5(2) + 6

= 10 - 10

= 0

= RHS = x² - 5x + 6

= (3)² - 5(3) + 6

= 9 - 15 + 6

= 15 – 15

 = 0

= RHS x = 2 and x = 3 both are the solutions of the given quadratic equation. 

(vi) Here,

Substituting the value x = - √2 and x = - 2√2 in

= 2 – 2 – 4

= – 4

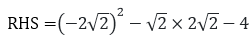
= 8 – 4 – 4

= 8 – 8

= 0

= RHS x = - 2√2 is the solution of the above mentioned quadratic equation. 

(vii) Here,

LHS = a²x² - 3abx + 2b² and RHS = 0

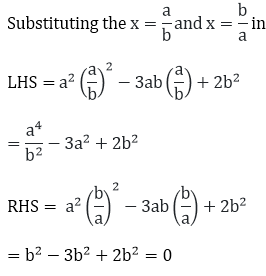
RHS = x = b/a

is the solution of the above mentioned quadratic equation. 

Question: 2

(i) Given that 2/3 is a root of the given equation. The equation is 7x² + kx - 3 = 0

(ii) Given that x=a is a root of the given equation x² - x(a + b) + k = 0

(iii)  Given that x = √2 is a root of the given equation kx² + √2x - 4

(iv) Given that x = - a is the root of the given equation x² + 3ax + k = 0

Solution:

(i) Given that 2/3 is a root of the given equation. The equation is 7x² + kx - 3 = 0

According to the question 2/3 satisfies the equation.

(ii) Given that x = a is a root of the given equation x² - x(a + b) + k = 0 = x = a satisfies the equation =  a²- a(a + b) + k = 0

= a² - a²- ab + k

K = ab

(iii) Given that x = √2 is a root of the given equation kx² + √2x - 4

x = √2 satisfies the given quadratic equation.

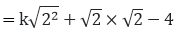
= 2k + 2 – 4 = 0

= 2k – 2 = 0

k = 1

(iv) Given that x= -a is the root of the given equation x² + 3ax + k = 0

Therefore, = (- a)² + 3a(- a) + k = 0

= a² + 3a² + k = 0

= k = 4a²= - a satisfies the equation 

Question: 3

Given to check whether 3 is a root of the equation

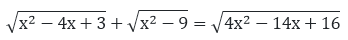
Solution:

= 0

Similarly putting x = 3 in

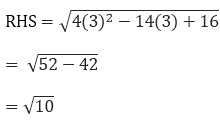
LHS ≠ RHS

x = 3 is not the solution the given quadratic equation.