Chapter 7: Statistics Exercise – 7.6
Question: 1
Draw an Ogive by less than the method for the following data:
| No. of rooms | No. of houses |
| 1 | 4 |
| 2 | 9 |
| 3 | 22 |
| 4 | 28 |
| 5 | 24 |
| 6 | 12 |
| 7 | 8 |
| 8 | 6 |
| 9 | 5 |
| 10 | 2 |
Solution:
| No. of rooms | No. of houses | Cumulative Frequency |
| Less than or equal to 1 | 4 | 4 |
| Less than or equal to 2 | 9 | 13 |
| Less than or equal to 3 | 22 | 35 |
| Less than or equal to 4 | 28 | 63 |
| Less than or equal to 5 | 24 | 87 |
| Less than or equal to 6 | 12 | 97 |
| Less than or equal to 7 | 8 | 107 |
| Less than or equal to 8 | 6 | 113 |
| Less than or equal to 9 | 5 | 119 |
| Less than or equal to 10 | 2 | 120 |
We need to plot the points (1, 4), (2, 3), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113), (9, 118), (10, 120), by taking upper class limit over the x-axis and cumulative frequency over the y-axis.

Question: 2
The marks scored by 750 students in an examination are given in the form of a frequency distribution table:
| Marks | No. of Students |
| 600 – 640 | 16 |
| 640 – 680 | 45 |
| 680 – 720 | 156 |
| 720 – 760 | 284 |
| 760 – 800 | 172 |
| 800 – 840 | 59 |
| 840 – 880 | 18 |
Solution:
| Marks | No. of Students | Marks Less than | Cumulative Frequency |
| 600 – 640 | 16 | 640 | 16 |
| 640 – 680 | 45 | 680 | 61 |
| 680 – 720 | 156 | 720 | 217 |
| 720 – 760 | 284 | 760 | 501 |
| 760 – 800 | 172 | 800 | 693 |
| 800 – 840 | 59 | 840 | 732 |
| 840 – 880 | 18 | 880 | 750 |
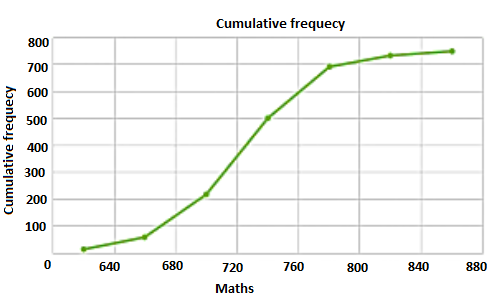
Plot the points (640, 16), (680, 61), (720, 217), (760, 501), (800, 673), (840, 732), (880, 750) by taking upper class limit over the x-axis and cumulative frequency over the y-axis.
Question: 3
Draw an Ogive to represent the following frequency distribution:
| Class-interval | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 |
| No. of students | 2 | 6 | 10 | 5 | 3 |
Solution:
The given frequency distribution is not continuous, so we will first make it continuous and then prepare the cumulative frequency:
| Class-interval | No. of Students | Less than | Cumulative frequency |
| 0.5 – 4.5 | 2 | 4.5 | 2 |
| 4.5 – 9.5 | 6 | 9.5 | 8 |
| 9.5 – 14.5 | 10 | 14.5 | 18 |
| 14.5 – 19.5 | 5 | 19.5 | 23 |
| 19.5 – 24.5 | 3 | 24.5 | 26 |
Plot the points (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23), (24.5,26) by taking the upper class limit over the x-axis and cumulative frequency over the y-axis.

Question: 4
The monthly profits (in Rs) of 100 shops are distributed as follows:
| Profit per shop | No of shops: |
| 0 – 50 | 12 |
| 50 – 100 | 18 |
| 100 – 150 | 27 |
| 150 – 200 | 20 |
| 200 – 250 | 17 |
| 250 – 300 | 6 |
Draw the frequency polygon for it
Solution:
We have
| Profit per shop | Mid-value | No of shops: |
| Less than 0 | 0 | 0 |
| Less than 0 – 60 | 25 | 12 |
| Less than 60 – 120 | 75 | 18 |
| Less than 120 – 180 | 125 | 27 |
| Less than 180 – 240 | 175 | 20 |
| Less than 240 – 300 | 225 | 17 |
| Less than 300 – 360 | 275 | 6 |
| Above 360 | 300 | 0 |

Question: 5
The following distribution gives the daily income of 50 workers of a factory:
| Daily income (in Rs): | No of workers: |
| 100 – 120 | 12 |
| 120 – 140 | 14 |
| 140 – 160 | 8 |
| 160 – 180 | 6 |
| 180 – 200 | 10 |
Convert the above distribution to a 'less than' type cumulative frequency distribution and draw its ogive.
Solution:
We first prepare the cumulative frequency table by less than method as given below:
| Daily income | Cumulative frequency |
| <120 | 12 |
| <140 | 26 |
| <160 | 34 |
| <180 | 40 |
| <200 | 50 |
Now we mark on x-axis upper class limit, y-axis cumulative frequencies. Thus we plot the point (120, 12), (140, 26), (160, 34), (180, 40), (200, 50).

Question: 6
The following table gives production yield per hectare of wheat of 100 farms of a village:
| Production yield: | No of farms: |
| 50 – 55 | 2 |
| 55 – 60 | 8 |
| 60 – 65 | 12 |
| 65 – 70 | 24 |
| 70 – 75 | 38 |
| 75 – 80 | 16 |
Draw 'less than' ogive and 'more than' ogive
Solution:
Less than method: Cumulative frequency table by less than method
| Production yield | Number of farms | Production yield more than | Cumulative frequency |
| 50 – 55 | 2 | 55 | 2 |
| 55 – 60 | 8 | 60 | 10 |
| 60 – 65 | 12 | 65 | 22 |
| 65 – 70 | 24 | 70 | 46 |
| 70 – 80 | 38 | 75 | 84 |
| 75 – 80 | 16 | 80 | 100 |
Now we mark on x-axis upper class limit, y-axis cumulative frequencies. We plot the point (50,100), (55, 98), (60, 90), (65, 78), (70, 54), (75, 16)

Question: 7
During the medical check-up of 35 students of a class, their weight recorded as follows:
| Weight (in kg) | No of students |
| Less than 38 | 0 |
| Less than 40 | 3 |
| Less than 42 | 5 |
| Less than 44 | 9 |
| Less than 46 | 14 |
| Less than 48 | 28 |
| Less than 50 | 32 |
| Less than 52 | 35 |
Draw a less than type ogive for the given data. Hence, obtain the median weight from the graph and verify the verify the result my using the formula.
Solution:
Less than method: It is given that On x-axis upper class limits. Y-axis cumulative frequency We plot the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 4), (48, 28), (50, 32), (52, 35).
More than method: cumulative frequency
| Weight | No. of students | Weight more than | Cumulative frequency |
| 38 – 40 | 3 | 38 | 34 |
| 40 – 42 | 2 | 40 | 32 |
| 42 – 44 | 4 | 42 | 30 |
| 44 – 46 | 5 | 44 | 26 |
| 46 – 48 | 14 | 46 | 21 |
| 48 – 50 | 4 | 48 | 7 |
| 50 – 52 | 3 | 50 | 3 |
x – axis lower class limits on y-axis cf We plot the points (38, 35), (40, 32), (42, 30), (44, 26), (46, 26), (48, 7), (50,3).

Question: 8
The following table shows the height of trees:
| Height | No. of trees |
| Less than 7 | 26 |
| Less than 14 | 27 |
| Less than 21 | 92 |
| Less than 28 | 134 |
| Less than 35 | 216 |
| Less than 42 | 287 |
| Less than 49 | 341 |
| Less than 56 | 360 |
Draw 'less than' ogive and 'more than' ogive
Solution:
By less than method
| Height | No. of trees |
| Less than 7 | 26 |
| Less than 14 | 27 |
| Less than 21 | 92 |
| Less than 28 | 134 |
| Less than 35 | 216 |
| Less than 42 | 287 |
| Less than 49 | 341 |
| Less than 56 | 360 |
Plot the points (7, 26), (14, 57), (21, 92), (28, 134), (35, 216), (42, 287), (49, 341), (56, 360) by taking upper class limit over the x-axis and cumulative frequency over the y-axis.
By more than method:
| Height | No. of trees | Height more than | C.F. |
| 0 – 7 | 26 | 0 | 360 |
| 7 – 14 | 27 | 5 | 334 |
| 14 – 21 | 92 | 10 | 303 |
| 21 – 28 | 134 | 15 | 268 |
| 28 – 35 | 216 | 20 | 226 |
| 35 – 42 | 287 | 25 | 144 |
| 42 – 49 | 341 | 30 | 73 |
| 49 – 56 | 360 | 35 | 19 |

Question: 9
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution:
| Profit (In lakhs In Rs) | Number of shops (frequency) |
| More than or equal to 5 | 30 |
| More than or equal to 10 | 28 |
| More than or equal to 15 | 16 |
| More than or equal to 20 | 14 |
| More than or equal to 25 | 10 |
| More than or equal to 30 | 7 |
| More than or equal to 35 | 3 |
Draw both ogive for the above data and hence obtain the median.
Solution:
More than method:
| Profit (In lakhs In Rs) | Number of shops (frequency) |
| More than or equal to 5 | 30 |
| More than or equal to 10 | 28 |
| More than or equal to 15 | 16 |
| More than or equal to 20 | 14 |
| More than or equal to 25 | 10 |
| More than or equal to 30 | 7 |
| More than or equal to 35 | 3 |
Now, we mark on x-axis lower class limits, y-axis cumulative frequency. Thus, we plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25,10), (30, 7) and (35, 3)
Less than method:
| Profit in lakhs | No of shops | Profits less than | C.F |
| 0 – 10 | 2 | 10 | 2 |
| 10 – 15 | 12 | 15 | 14 |
| 15 – 20 | 2 | 20 | 16 |
| 20 – 25 | 4 | 25 | 20 |
| 25 – 30 | 3 | 30 | 23 |
| 30 – 35 | 4 | 35 | 27 |
| 35 – 40 | 3 | 40 | 30 |
Now we mark the upper class limits along x-axis and cumulative frequency along y-axis. Thus we plot the points (10, 2), (15,14), (20,16), (25, 20), (30, 23), (35, 27), (40, 30).
We find that the two types of curves intersect of P from point L it is drawn on x-axis The value of a profit corresponding to M is 17.5. Hence median is 17.5 lakh
