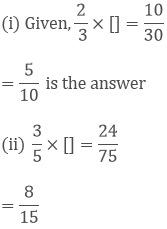Chapter 1: Fractions Exercise – 2.1
Question: 1
Compare the following fractions by using the symbol > or < or =;
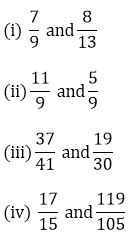
Solution:
(i) We have,
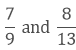
Taking the LCM of 9 and 13, we get,
9 x 13 = 117
Now, we convert the given fractions to equivalent fractions by making the denominators 117,
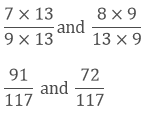
As we know, 91 > 72
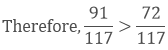
Hence, 79 > 813
(ii) We have,
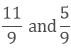
The given fractions are equivalent fractions as the denominators are equal,
And we know that, 11 > 5
Therefore, 119 > 59
(iii) We have,
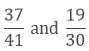
Taking the LCM of 41 and 30, we get,
41 x 30 = 1230
Now, we convert the given fractions to equivalent fractions by making the denominators 1230,
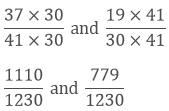
Now, we clearly know 1110 > 779
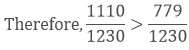
Hence, 3741 > 1930
(iv) We have,
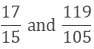
Taking the LCM of 15 and 105, we get,
5 x 3 x 7 = 105
Now, we convert the given fractions to equivalent fractions by making the denominators 105,
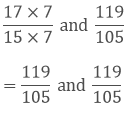
Question: 2
Arrange the following fractions in ascending order:
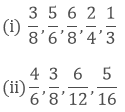
Solution:
(i) We have,
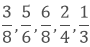
Taking the LCM of 8, 6, 8, 4 and 3, we get,
2 x 4 x 3 = 24
Now, we convert the given fractions to equivalent fractions by making the denominators 24,
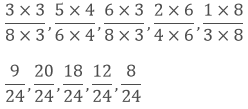
We know that, 8 < 9 < 12 < 18 < 20
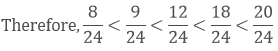
Hence, 13 < 38 < 24 < 68 < 56
(ii) We have,
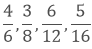
Taking the LCM of 6, 8, 12 and 16, we get,
2 x 2 x 2 x 2 x 3 = 48
Now, we convert the given fractions to equivalent fractions by making the denominators 48,
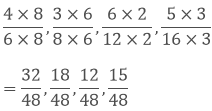
We know that, 12 < 15 < 18 < 32
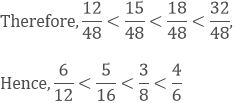
Question: 3
Arrange the following fractions in descending order:
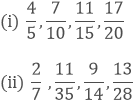
Solution:
(i) We have,
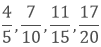
Taking the LCM of 5, 10, 15 and 20, we get,
5 x 2 x 2 x 3 = 60
Now, we convert the given fractions to equivalent fractions by making the denominators 48
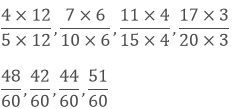
As we know 51 > 48 > 44 > 42
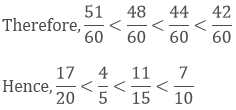
(ii) We have,
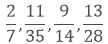
Taking the LCM of 7, 35, 14 and 28, we get,
7 x 5 x 2 x 2 = 140
Now, we convert the given fractions to equivalent fractions by making the denominators 140
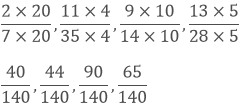
As we know 40 > 44 > 65 > 90
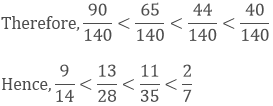
Question: 4
Write the equivalent fractions of 3/5
Solution:
Multiplying or dividing both the numerator and denominator by the same number,
so that the fraction keeps its value.
So the equivalent fractions of 3/5 are
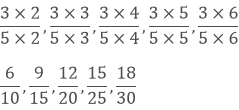
are the five equivalent fractions of 3/5
Question: 5
Find the sum:
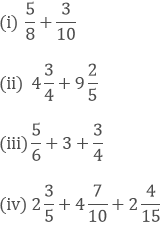
Solution:
(i) We have,
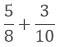
Taking the LCM of 8 and 10, we get,
2 x 4 x 5 = 40
Now, we convert the given fractions to equivalent fractions by making the denominators 40
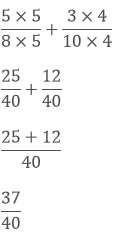
(ii) We have,
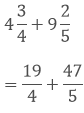
Taking out the LCM of 4 and 5, we get,
4 x 5 = 20
Now, we convert the given fractions to equivalent fractions by making the denominators 20
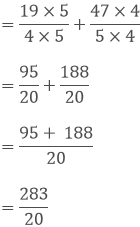
(iii) We have,
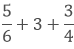
Taking out the LCM of 6 and 4, we get,
2 x 2 x 3 = 12
Now, we convert the given fractions to equivalent fractions by making the denominators 12
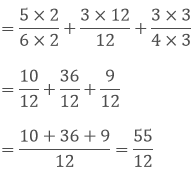
(iv) We have,
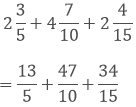
Taking out the LCM of 5, 10 and 15, we get,
5 x 2 x 3 = 30
Now, we convert the given fractions to equivalent fractions by making the denominators 30
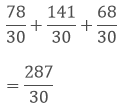
Question: 6
Find the difference of
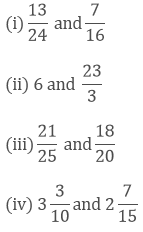
Solution:
(i) We have,
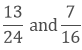
Taking out the LCM of 24 and 16, we get,
2 x 2 x 2 x 2 x 3 = 48
Now, we convert the given fractions to equivalent fractions by making the denominators 48
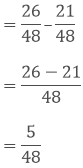
(ii) We have, 6 and 23/3
The difference between 6 and 23/3
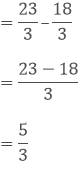
(iii) We have,
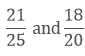
Taking out the LCM of 25 and 20, we get,
5 x 5 x 4 = 100
Now, we convert the given fractions to equivalent fractions by making the denominators 100
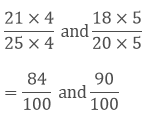
The difference between both the fractions are
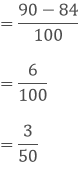
(iv) We have,
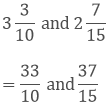
Taking out the LCM of 10 and 15, we get,
2 x 3 x 5 = 30
Now, we convert the given fractions to equivalent fractions by making the denominators 30
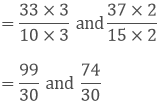
The difference between both the fractions are
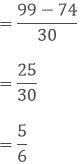
Question: 7
Find the difference:
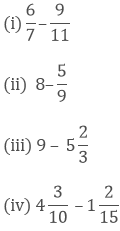
Solution:
(i) We have,
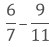
Taking out the LCM of 7 and 11, we get,
7 x 11 = 77
Now, we convert the given fractions to equivalent fractions by making the denominators 77
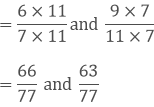
The difference between both the fractions are
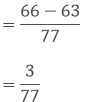
(ii) We have,
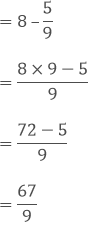
(iii) We have,
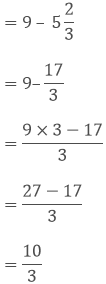
(iv) We have,
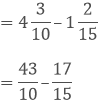
Taking out the LCM of 10 and 15, we get,
2 x 3 x 5 = 30
Now, we convert the given fractions to equivalent fractions by making the denominators 30
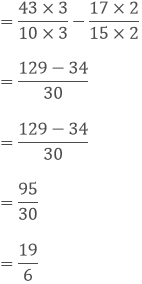
Question: 8
Simplify:
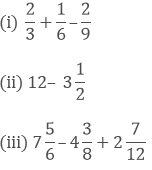
Solution:
(i) We have,
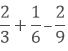
Taking out the LCM of 3, 6 and 9, we get,
3 x 3 x 2 = 18
Now, we convert the given fractions to equivalent fractions by making the denominators 18, we get,
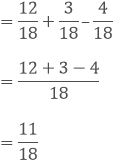
(ii) We have,
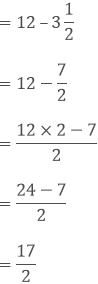
(iii) We have,
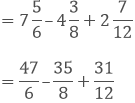
Taking out the LCM of 6, 8 and 12, we get,
2 x 2 x 2 x 3 = 48
Now, we convert the given fractions to equivalent fractions by making the denominators 48, we get,
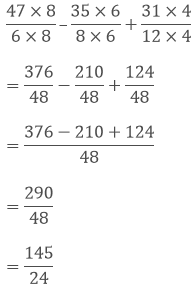
Question: 9
What should be added to to get 12?
to get 12?
Solution:
We have,
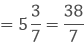
Let x be the number added to 38/7 to get 12
Therefore,
x + 387 = 12
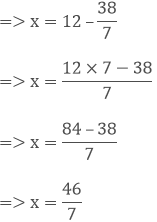
Question: 10
What should be added to ?
?
Solution:
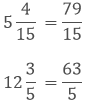
Let x be the number added to 79/15 to get 63/5
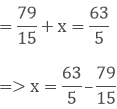
Taking out the LCM of 5 and 15, we get,
3 x 5 = 15
Now, we convert the given fractions to equivalent fractions by making the denominators 15, we get,
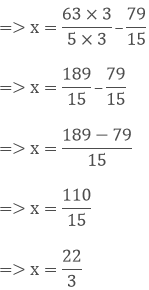
Question: 11
Suman studies for hours daily. She devotes
hours daily. She devotes hours of her time for science and mathematics. How much time does she devote for other subjects?
hours of her time for science and mathematics. How much time does she devote for other subjects?
Solution:
Given,
Suman studies for hours daily
hours daily
She devotes hours of her time for science and mathematics. Let x be time she devotes for other subjects.
hours of her time for science and mathematics. Let x be time she devotes for other subjects.
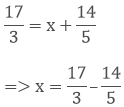
Taking out the LCM of 3 and 5, we get,
3 x 5 = 15
Now, we convert the given fractions to equivalent fractions by making the denominators 48, we get,
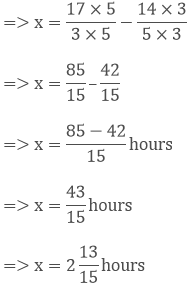
Question: 12
A piece of wire of length If it is cut into two pieces in such a way that the length of one piece is
If it is cut into two pieces in such a way that the length of one piece is what is the length of the other piece?
what is the length of the other piece?
Solution:
A piece of wire of length one piece is
one piece is
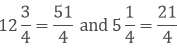
Let the length of other piece be x m.
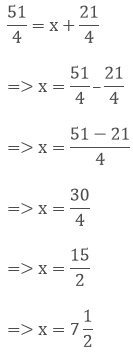
Question: 13
A rectangular piece of paper is long and
long and wide. Find its perimeter?
wide. Find its perimeter?
Solution:
Given,
A rectangular piece of paper is long and
long and wide
wide
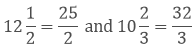
Perimeter = 2(length + width)

Question: 14
In a “magic square”, the sum of numbers in each row, in each column and along the diagonal is same. Is this a “magic square”?
| 4/11 | 9/11 | 2/11 |
| 3/11 | 5/11 | 7/11 |
| 8/11 | 1/11 | 6/11 |
Solution:
Given,
| 4/11 | 9/11 | 2/11 |
| 3/11 | 5/11 | 7/11 |
| 8/11 | 1/11 | 6/11 |

Therefore, the sum of numbers in each row, in each column and along the diagonal is same and the sum is 15/11.
Question: 15
The cost of Mathematics book is Rs and that of science book is
and that of science book is Which costs more and by how much?
Which costs more and by how much?
Solution:
Given,
The cost of Mathematics book is Rs and that of science book is
and that of science book is
We need to compare the cost of mathematics and science book,
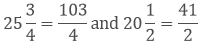
Taking out the LCM of 4 and 2, we get,
2 x 2 = 4
Now, we convert the given fractions to equivalent fractions by making the denominators 4, we get
= 103/4
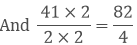
As we know, 103 > 82
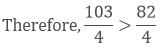
Hence, the cost of mathematics book is more than that of the cost of the science book.
Question: 16
Provide the number in the box [] and also give its simplest form in each of the following:
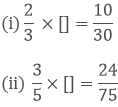
Solution: