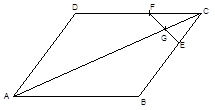Orthogonal System of Vectors
Table of Content |
 In the orthogonal system of vectors we choose these vectors as three mutually perpendicular unit vectors denoted by
In the orthogonal system of vectors we choose these vectors as three mutually perpendicular unit vectors denoted by ![]() , and
, and ![]() directed along the
directed along the
positive directions of X, Y and Z axes respectively.
Corresponding to any point P(x, y z) we can associate a vector w.r.t. a fixed orthogonal system and then this vector is the position vector (p.v.) of that point. i.e. p.v. of P = ![]()
Distance of P from O = ![]() =
= ![]()
x, y, z are called the components of the vector
Section Formula
Internal Division
Let A and B be two points with position vectors ![]() and
and ![]() respectively, and C be a point dividing AB internally in the ratio m : n. Then the position vector of C is given by
respectively, and C be a point dividing AB internally in the ratio m : n. Then the position vector of C is given by ![]() .
.
|
Proof: Let O be the origin. The
Þ n. Þ n(P.V. of Þ Þ |
External Division
Let A and B be two points with position vectors ![]() and
and ![]() respectively and let C be a point dividing
respectively and let C be a point dividing ![]() externally in the ratio m : n. Then the position vector of
externally in the ratio m : n. Then the position vector of ![]() is given by
is given by![]() .
.
Note:
(i) If C is the mid–point of AB, then P.V. of C is ![]() .
.
(ii) We have,![]() . Hence
. Hence ![]() is in the form of
is in the form of ![]() .
.
where, ![]() and
and ![]() .Thus, position vector of any point
.Thus, position vector of any point ![]() on
on ![]() can always be taken as
can always be taken as ![]() where l + m = 1.
where l + m = 1.
(iii) If circumcentre is origin and vertices of a triangle have position vectors ![]() , then the position vector of orthocentre will be
, then the position vector of orthocentre will be ![]() .
.
Illustration 4: ABC is a triangle. A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
Solution: Take the vertex A of the triangle ABC as the origin. Let ![]() be the p.v. of B and C. The mid point of BC has the p.v. =
be the p.v. of B and C. The mid point of BC has the p.v. = ![]() The equation of the median is
The equation of the median is ![]() . Let D divide AB in the ratio 1:m
. Let D divide AB in the ratio 1:m
Þ p.v. of ![]() .Let E divide AC in the ratio 1:l
.Let E divide AC in the ratio 1:l
Þ p.v. E = ![]() Þl = m. p.v. of the mid-point of DE =
Þl = m. p.v. of the mid-point of DE = ![]() which lies on the median. Hence the median bisects DE.
which lies on the median. Hence the median bisects DE.
Isector of the Angle Between Two Vectors
Consider two non–zero, non–collinear vectors ![]() and
and ![]() . The bisector of the angle between the two vectors
. The bisector of the angle between the two vectors ![]() and
and ![]() is k
is k
where k Î R+.
Illustration 5: If the vector ![]() bisects the angle between
bisects the angle between ![]() and
and ![]() , where
, where ![]() is a unit vector then find
is a unit vector then find ![]() .
.
Key concept: Bisector of the angle between the two vectors ![]() and
and ![]() is k
is k where k Î R+.
where k Î R+.
Solution: According to the given conditions l![]() =
= ![]()
Þ 3![]() = 3l
= 3l![]()
= ![]() (3l + 1) –
(3l + 1) – ![]() (2 + 9l) +
(2 + 9l) + ![]() (15l – 2)
(15l – 2)
Þ ![]()
Þ 9 = (3l + 1)2 + (2 + 9l)2 + (15l – 2)2
Þ 315l2 – 18l = 0 Þl = 0, ![]() .
.
If l = 0, ![]() (not acceptable)
(not acceptable)
For l = ![]() ,
, ![]()
Scalar (or Dot) Product of Two Vectors
|
The scalar product of
Geometrical Interpretation: |
![]() is the product of length of one vector and length of the projection of the other vector in the direction of former.
is the product of length of one vector and length of the projection of the other vector in the direction of former.
![]() . Projection of
. Projection of ![]() in direction of
in direction of ![]() =
=![]() .Projection of
.Projection of ![]() in direction of
in direction of ![]()
Properties:
![]() Þ
Þ![]()
![]()
![]()
![]() (acosq)b = (projection of
(acosq)b = (projection of ![]() ) b = (projection of
) b = (projection of ![]() ) a
) a
![]() (Distributive law)
(Distributive law)
![]()
![]() Û
Û![]() are perpendicular to each other Þ
are perpendicular to each other Þ![]()
![]() =
= ![]()
![]()
If ![]() then
then![]()
If ![]() are non-zero, the angle between them is given by
are non-zero, the angle between them is given by ![]()
= ![]()
Illustration 6: Prove by vector method that (a1b1 + a2b2 + a3b3)2 £ (a12+ a22 + a32) (b12 + b22 + b32).
Solution: Let ![]() = a1
= a1![]() + a2
+ a2![]() + a3
+ a3![]() and
and ![]() =
= ![]() .
.
Now ![]() ×
×![]() = a1 b1 + a2b2 + a3b3 , also
= a1 b1 + a2b2 + a3b3 , also ![]() ×
×![]() = |
= |![]() | |
| |![]() | cosq£ |
| cosq£ |![]() | |
| |![]() |.
|.
Þ (![]() ×
×![]() )2£ |
)2£ |![]() |2 |
|2 |![]() |2 Þ (a1b1 + a2b2 + a3b3)2£
|2 Þ (a1b1 + a2b2 + a3b3)2£![]()
Illustration 7: If |![]() | = 3, |
| = 3, |![]() | = 1, |
| = 1, |![]() | = 4 and
| = 4 and ![]() , find the value of
, find the value of ![]()
Solution: We know, ![]()
Þ 0 = ![]() (Given
(Given ![]() )
)
Þ0 = ![]()
Þ![]() = –
= –![]() = –13
= –13
Illustration 8: In a DABC, prove by vector method that
cos 2A + cos 2B + cos 2C ³ –3/2
Solution: As we know; ![]() …(i)
…(i)
and ![]() … (ii)
… (ii)
![]()
Þ 3R2 + 2R2 (cos 2A + cos2B + cos 2C) ³ 0
Þ cos 2A + cos 2B + cos 2C ³ –3/2
Vector (Or Cross) Product of Two Vectors
|
The vector product of two vectors |
If we curl the fingers of our right hand from ![]() to
to ![]() through the smaller angle (keeping the initial point of
through the smaller angle (keeping the initial point of ![]() and
and ![]() same), the thumb points in the direction of
same), the thumb points in the direction of ![]() . In this case,
. In this case, ![]() ,
,![]() and
and ![]() (or
(or ![]() ), in that order are said to form a right handed system. It is evident that
), in that order are said to form a right handed system. It is evident that ![]() = absinq.
= absinq.
Properties:
-
 Þ
Þ
-
 (non-commutative)
(non-commutative) -
 (Distributive)
(Distributive) -

-
 Û
Û are collinear (if none of
are collinear (if none of  is a zero vector)
is a zero vector) -

-

-
If
 then
then 
-
=

- Any vector perpendicular to the plane of
 is l (
is l ( ) where l is a real number. Unit vector perpendicular to
) where l is a real number. Unit vector perpendicular to  is ±
is ± 
|
Area is also treated as a vector with its direction in the proper sense. |
Illustration 9: ![]() and
and ![]() are unit vectors and || = 4. If angle between
are unit vectors and || = 4. If angle between ![]() and
and ![]() is cos–1
is cos–1![]() and
and ![]() , then show that
, then show that![]() can be written as
can be written as ![]() also find the value of l.
also find the value of l.
Key concept: If ![]() , then it can be written as
, then it can be written as ![]() =0, that means vector
=0, that means vector ![]() and (
and (![]() -2
-2![]() ) are collinear.
) are collinear.
Solution: Since vector ![]() and (
and (![]() -2
-2![]() ) are collinear, vector
) are collinear, vector ![]() can be written as
can be written as![]() Þ
Þ![]()
![]()
Þ ![]() Þ16 + 4 – 4(4) (1)
Þ16 + 4 – 4(4) (1) ![]() = l2(1)
= l2(1)
Þ l2 = 16 Þl± 4.
Illustration 10: If ![]() ,
, ![]() ,
, ![]() are three vectors such that
are three vectors such that ![]() ,
, ![]() , then show that
, then show that ![]() = 1,
= 1, ![]()
Solution: Given ![]() …(i)
…(i)
![]() …(ii)
…(ii)
(1) – (2) Þ![]()
Þ ![]()
Now either ![]() is perpendicular to
is perpendicular to ![]() which is not possible
which is not possible
Or ![]() = 0 Þ
= 0 Þ![]() .
.
Also ![]() Þ
Þ![]() .
. ![]()
Equation the coefficients of ![]() , we get
, we get ![]() .
.
Thus ![]() and
and ![]() .
.
Scalar Triple Product
|
It is defined for three vectors i.e. V = magnitude of |
The value of scalar triple product depends on the cyclic order of the vectors and is independent of the position of the dot and cross. These may be interchange at pleasure. However and anti-cyclic permutation of the vectors changes the value of triple product in sign but not a magnitude.
Properties:
-
If
 are given as
are given as  etc., then
etc., then 
-
 i.e. position of dot and cross can be interchanged without altering the product. Hence it is also represented by
i.e. position of dot and cross can be interchanged without altering the product. Hence it is also represented by 
|
· · · |
-
 in that order form a right handed system if
in that order form a right handed system if 
Illustration 11: Show that ![]() .
.
Key concept: In such type of questions first we reduce each term as a product of two or three vector, by substituting a group of vectors by a single vector and then solve.
Solution: Let ![]()
Now L.H.S. = ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= 0 = R.H.S.
Vector Triple Product
The vector product of two vectors, one of which is itself the vector product of two vectors, is a vector quantity called vector triple product.
It is defined for three vectors ![]() as the vector
as the vector ![]() . This vector being perpendicular to
. This vector being perpendicular to ![]() , is coplanar with
, is coplanar with ![]() i.e.
i.e. ![]()
Take the scalar product of this equation with a. We get
0 = ![]() Þ
Þ![]()
If we choose the coordinate axes in such a way that
![]() , it is easy to show that l = 1. Hence
, it is easy to show that l = 1. Hence
![]()
In general, ![]() ( Vector triple product is not associative ) .
( Vector triple product is not associative ) .
![]() , if some or all of
, if some or all of ![]() are zero vectors or
are zero vectors or ![]() are collinear.
are collinear.
Illustration 12: Let ![]() be three mutually perpendicular vectors of the same magnitude. If the vector
be three mutually perpendicular vectors of the same magnitude. If the vector ![]() satisfy the equation
satisfy the equation
![]() then find
then find ![]()
Solution: Here ![]() -
-
{![]()
or l2![]()
where ![]()
l2 { ![]()
Þl2 {3![]() Þ3
Þ3![]()
Hence ![]() .
.
Collinear and Coplanar Vectors
1. Methods to Prove Collinearity
-
Two vectors
 and
and  are collinear if there exists kÎR such that
are collinear if there exists kÎR such that  .
. -
If
 are collinear.
are collinear. -
Three points A(
 ), B(
), B( ), C(
), C( )are collinear if there exists kÎR such that
)are collinear if there exists kÎR such that  that is
that is  .
. -
If
 then A, B, C are collinear.
then A, B, C are collinear. -
A(
 ), B(
), B( ), C(
), C( ) are collinear if there exists scalars l, m, n, (not all zero) such that
) are collinear if there exists scalars l, m, n, (not all zero) such that  where l + m + n = 0.
where l + m + n = 0.
All the above methods are equivalent and any of them can be utilized to prove the collinearity. (of 2 vectors or 3 points)
Illustration 13: Let ![]() be three non–zero vectors such that any two of them are non–collinear. If
be three non–zero vectors such that any two of them are non–collinear. If ![]() is collinear with
is collinear with ![]() and
and ![]() is collinear with
is collinear with ![]() , then prove that
, then prove that ![]() .
.
Key concept: Two vectors ![]() and
and ![]() are collinear if there exists kÎR such that
are collinear if there exists kÎR such that ![]() .
.
Solution: It is given that ![]() is collinear with
is collinear with ![]()
Þ![]() for some scalar l …(i)
for some scalar l …(i)
Also ![]() is collinear with
is collinear with ![]()
Þ![]() for some scalar m …(ii)
for some scalar m …(ii)
from (i) and (ii)
Þ(1 + 2m) ![]() + (3 – ml)
+ (3 – ml) ![]() = 0
= 0
Þ1 + 2m = 0 and 3 – ml = 0 {![]()
![]() and
and ![]() are non–collinear vectors}
are non–collinear vectors}
Þ m = – 1/2 and l = – 6
Substituting the values of l and m in (i) & (ii), we get
![]()
2. Methods to Prove Coplanarity
-
Three vectors
 are coplanar if there exists l, mÎR such that
are coplanar if there exists l, mÎR such that  i.e., one can be expressed as a linear combination of the other two.
i.e., one can be expressed as a linear combination of the other two. -
If
 are coplanar (necessary and sufficient condition).
are coplanar (necessary and sufficient condition). -
Four points A
 , B
, B , C
, C and D
and D lie in the same plane if there exist l, mÎR such that
lie in the same plane if there exist l, mÎR such that  i.e.
i.e.  .
. -
If
 = 0 then A, B, C, D are coplanar.
= 0 then A, B, C, D are coplanar. -
A, B, C, D are coplanar if there exists scalars k, l, m, n (not all zero), such that
 where k + l + m + n = o.
where k + l + m + n = o.
Again all the above methods are equivalent. Choose the best amongst them depending on convenience.
Illustration 14: Prove that if cos a¹ 1, cosb¹ 1 and cos g¹ 1, then the vectors ![]()
![]() can never be coplanar.
can never be coplanar.
Key concept: If three vectors![]() are coplanar then
are coplanar then ![]() .
.
Solution: Suppose that ![]() are coplanar.
are coplanar.
Þ  ( R2® R2 – R1 and R3® R3 – R1 )
( R2® R2 – R1 and R3® R3 – R1 )
or 
or cosa (cosb – 1)(cosg – 1) – (1 – cosa)(cosg – 1) – (1 – cosa)(cosb – 1) = 0
dividing through out by (1 – cosa) (1 – cosb)(1 – cosg); we get
![]()
or –1 + ![]()
Þ ![]()
as ![]()
Hence they can not be coplanar
Applications of Vectors
1. Vector Equation of a Straight Line
|
Following are the two most useful forms of the equation of a line. (i) Line passing through a given point A |
where ![]() is the p.v. of any general point P on the line and l is any real number. The vector equation of a straight line passing through the origin and parallel to a vector
is the p.v. of any general point P on the line and l is any real number. The vector equation of a straight line passing through the origin and parallel to a vector ![]() is
is ![]() = n
= n ![]() .
.
|
(ii) Line passing through two given points A For each particular value of l, we get a particular point on the line. Each of the above equations can be written easily in Cartesian form also. For example, in case (i), writing
|
we get ![]()
Þ x = a1 + lb1, y = a2 + lb2, z = a3 + lb3.
Illustration 15: Given vectors ![]() where O is the centre of circle circumscribed about DABC, then find vector
where O is the centre of circle circumscribed about DABC, then find vector ![]() .
.
Solution: Here, ![]()
Þ![]() and
and ![]()
|
Now Þ or Þ Þ |
Now if we take ![]() then from (i),
then from (i),
![]() …(ii)
…(ii)
and ![]() …(iii)
…(iii)
\ Solving (ii) and (iii);
![]() and
and ![]()
Þ ![]()
2. Shortest Distacne Between Two Lines
Two lines in space can be parallel, intersecting or neither (called skew lines). Let ![]() be two lines.
be two lines.
(i) They intersect if ![]() .
.
(ii) They are parallel if ![]() are collinear. Parallel lines are of the form
are collinear. Parallel lines are of the form ![]() Perpendicular distance between them is constant and is equal to
Perpendicular distance between them is constant and is equal to ![]() .
.
(iii) For skew lines, shortest distance between them (along common perpendicular) is given by ![]() .
.
3. Equation of a Plane in Vector Form
|
Following are the four useful ways of specifying a plane. (i) A plane at a perpendicular distance d from the origin and normal to a given direction or
|
|
|
(ii) A plane passing through the point A |
(iii) Parameteric equation of the plane passing through A![]() and parallel to the plane of vectors
and parallel to the plane of vectors ![]() is given by
is given by ![]() Þ.
Þ.![]()
(iv) Parameteric equation of the plane passing through A![]() , B
, B![]() C
C![]() (A, B, C non-collinear) is given by
(A, B, C non-collinear) is given by ![]() Þ
Þ![]() .
.
In Cartesian form, the equation of the plane assumes the form Ax + By + Cz = D. The vector normal to this plane is ![]() and the perpendicular distance of the plane from the origin is
and the perpendicular distance of the plane from the origin is ![]() .
.
Angle Between a Line and a Plane:
The angle between a line and a plane is the complement of the angle between the line and the normal to the plane.
Angle Between Two Planes:
It is equal to the angle between their normal unit vectors ![]() . i.e. cosq =
. i.e. cosq = ![]()
4. Some Miscellaneous Result
|
(i) Volume of the tetrahedron ABCD =
|
|
|
(ii) Area of the quadrilateral with diagonals
|
5. Reciprocal System of Vectors
If ![]() are three non-coplanar vectors, then a system of vectors
are three non-coplanar vectors, then a system of vectors ![]() defined by
defined by ![]() is called the reciprocal system of vectors because
is called the reciprocal system of vectors because ![]() .
.
Further ![]()
![]()
The scalar product of any vector of one system with a vector of other system which does not correspond to it is zero i.e.
![]()
If ![]() is a reciprocal system to
is a reciprocal system to ![]() then
then ![]() is also reciprocal system to
is also reciprocal system to ![]() .
.
Illustration 16: Show that the points ![]() and
and ![]() are equi-distant from the plane r × (5i + 2j – 7k) + 9 = 0 and are on the opposite sides of it.
are equi-distant from the plane r × (5i + 2j – 7k) + 9 = 0 and are on the opposite sides of it.
Solution: The given plane is ![]() = -9
= -9
Length of the perpendicular from ![]() to it is
to it is
![]()
Length of the perpendicular from ![]()
= ![]()
Thus the length of the two perpendiculars are equal in magnitude but opposite in sign. Hence they are located on opposite sides of the plane.
Solved Objective Problems
Q1. Any four non-zero vector will always be:
(A) Linearly dependent (B) Linearly independent
(C) Either ‘A’ or ‘B’ (D) None of these
Sol. Four or more than four non zero vectors are always linearly dependent.
Hence (A) is correct answer.
Q2. If ![]() and
and ![]() are reciprocal vectors, then:
are reciprocal vectors, then:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) None of these
(D) None of these
Sol. If ![]() and
and ![]() are reciprocal, then
are reciprocal, then
![]() and
and ![]()
![]()
![]()
![]()
![]()
Hence (C) is correct answer.
Q3. If ![]() and
and ![]() , then:
, then:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
![]()
![]()
![]()
Also, ![]()
![]()
![]()
![]()
Thus ![]()
Hence (C) is correct answer.
Q4. If three unit vectors ![]() satisfy
satisfy ![]() , then angle between
, then angle between ![]() and
and ![]() is:
is:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
![]() = 1
= 1
![]()
![]()
![]()
![]()
![]()
Hence (B) is correct answer.
Q5. Projection of ![]() on
on ![]() is equal to:
is equal to:
(A) 3 (B) -3
(C) 9 (D) -9
Sol. Projection of ![]() on
on ![]() is
is ![]()
Thus required projection
= ![]()
= ![]()
Hence (B) is correct answer.
Q6. If ![]() and
and ![]() are two non-collinear unit vectors, then projection of
are two non-collinear unit vectors, then projection of ![]() on
on ![]() is equal to:
is equal to:
(A) 2 (B) -2
(C) 1 (D) None of these
Sol. ![]()
Thus projection of ![]() on
on ![]() is zero.
is zero.
Hence (D) is correct answer.
Q7. ABCD is a parallelogram with ![]() and
and ![]() . Area of this parallelogram is equal to:
. Area of this parallelogram is equal to:
(A) ![]() sq. units (B)
sq. units (B) ![]() sq. units
sq. units
(C) ![]() sq. units (D)
sq. units (D) ![]() sq. units
sq. units
Sol. Area vector of parallelogram
= ![]()
= 
= ![]()
= ![]()
![]() Area of the parallelogram
Area of the parallelogram
= ![]() sq. units
sq. units
Hence (B) is correct answer.
Q8. If ![]() and
and ![]() always make an acute angle with each other for every value of
always make an acute angle with each other for every value of ![]() , then:
, then:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
= x(x + 1) + x – 1 + a
= ![]() + 2x + a – 1
+ 2x + a – 1
We must have
![]()
![]() + 2x + a – 1 > 0
+ 2x + a – 1 > 0 ![]()
![]() 4 – 4(a – 1) < 0
4 – 4(a – 1) < 0
![]() a > 2
a > 2
Hence (B) is correct answer.
Q9. Let ![]() be three non zero vectors such that
be three non zero vectors such that ![]() Then
Then ![]() , where
, where ![]() is equal to:
is equal to:
(A) 1 (B) 2
(C) -1 (D) -2
Sol. Clearly ![]() and
and ![]() represents the sides of a triangle.
represents the sides of a triangle.
It’s area vector,
![]()
![]()
Thus, ![]()
![]()
![]()
Hence (D) is correct answer.
Q10. If ![]() ,
, ![]() where
where ![]() , then:
, then:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
Taking cross with ![]() in first equation, we get
in first equation, we get
![]()
![]()
![]() and
and ![]()
Also, ![]()
![]()
![]()
Hence (A) is correct answer.
Q11. Let ![]() be unit vectors such that
be unit vectors such that ![]() ,
, ![]() ,
, ![]() ,
, ![]() Then angle between
Then angle between ![]() and
and ![]() is :
is :
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
Taking dot with ![]() on both sides, we get
on both sides, we get
![]()
![]()
![]()
If ![]() be the angle between
be the angle between ![]() and
and ![]() then
then
![]()
![]()
![]()
Hence (B) is correct answer.
Q12. Let ![]() be pair wise mutually perpendicular vectors, such that
be pair wise mutually perpendicular vectors, such that ![]() . Then length of
. Then length of ![]() is equal to:
is equal to:
(A) 2 (B) 4
(C) 3 (D) 6
Sol. ![]()
= ![]()
= ![]()
= 1 + 4 + 4 + 0 + 0 + 0
= 9
![]()
![]() = 3
= 3
Hence (C) is correct answer.
Q13. Let ![]() be three unit vectors such that
be three unit vectors such that ![]() Then
Then ![]() is equal to:
is equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) None of these
(D) None of these
Sol. ![]()
Thus ![]() are coplaner.
are coplaner.
Hence ![]()
Hence (D) is correct answer.
Q14. ABCD is a parallelogram ![]() and
and ![]() are the midpoints of side BC and CD respectively. If
are the midpoints of side BC and CD respectively. If ![]() , then
, then ![]() is equal to:
is equal to:
(A) 1/2 (B) 1
(C) 3/2 (D) 2
Sol. Let P.V. of A,B,D be ![]() and
and ![]() respectively.
respectively.
Then P.V. of C = ![]()
Also, P.V. of ![]()
and, P.V. of ![]()
![]()
Hence (C) is correct answer.
Q15. Two constant force ![]() and
and ![]() act on a particle. If particle is displaced from a point A with position vector
act on a particle. If particle is displaced from a point A with position vector ![]() to the point B with position vector
to the point B with position vector ![]() Then work done in the process is equal to:
Then work done in the process is equal to:
(A) 15 units (B) 10 units
(C) -15 units (D) -10 units
Sol. Total force, ![]()
Displacement, ![]()
![]()
Work done = ![]()
= 2 – 12 – 5 = - 15 units.
Hence (C) is correct answer.
Q16. A, B, C and D are any four points in the space. If ![]()
![]() , where
, where ![]() is the area of triangle ABC, then
is the area of triangle ABC, then ![]() is equal to:
is equal to:
(A) 2 (B) 1/2
(C) 4 (D) 1/4
Sol. Let P.V. of A, B, C and D be ![]() and
and ![]()
![]()
![]() ,
,
![]()
and ![]()
![]()
![]()
![]()
= ![]()
= ![]()
= ![]()
= 2(![]() )
)
![]()
![]()
= 4![]()
= 4![]()
Hence (C) is correct answer.
Q17. The position vector of the points A, B, C and D are ![]() ,
, ![]() ,
, ![]() and
and ![]() . It is known that these points are coplanar, then
. It is known that these points are coplanar, then ![]() is equal to:
is equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) None of these
(D) None of these
Sol. ![]()
![]()
![]()
If vector ![]() and
and ![]() are coplanar, then
are coplanar, then

![]()
Hence (A) is correct answer.
Q18. Let ![]() be any three vectors. Then
be any three vectors. Then ![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) Zero (D) None of these
Sol. ![]()
![]()
![]()
![]()
![]()
Hence (B) is correct answer.
Q19. Let ![]() be any three vectors. Then
be any three vectors. Then ![]() is also equal to:
is also equal to:
(A) ![]() (B)
(B) ![]()
(C) Zero (D) None of these
Sol. ![]()
![]()
![]()
![]()
Hence (A) is correct answer.
Q20. ![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
Similarly, ![]()
and ![]()
![]()
![]()
![]()
Hence (C) is correct answer.
Q21. Value of ![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) None of these
(D) None of these
Sol. ![]()
![]()
![]()
![]()
Hence (A) is correct answer.
Q22. For any four vectors ![]() the expression
the expression ![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) None of these
(D) None of these
Sol. ![]()
![]()
![]()
![]() = 0
= 0
Hence (D) is correct answer.
Q23. For any four vectors ![]() and
and ![]()
![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
![]()
![]()
![]()
![]()
![]()
Hence (B) is correct answer.
Q24. In the parallelogram ABCD if the internal bisectors of the angle ![]() and
and ![]() intersect at the point P, then
intersect at the point P, then ![]() is equal to:
is equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. Let P.V. of B, A and C be ![]() and
and ![]() respectively.
respectively.
Now, ![]() and
and ![]()
![]()
![]()
Hence (D) is correct answer.
Q25. If the vector ![]() bisects the angle between
bisects the angle between ![]() and
and ![]() , where
, where ![]() is a unit vector, then:
is a unit vector, then:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. We must have
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For ![]() (not acceptable)
(not acceptable)
For ![]()
Hence (D) is correct answer.
Q26. Distance of ![]() from the plane
from the plane ![]() is:
is:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) None of these
(D) None of these
Sol. Let Q(![]() ) be the foot of altitude drawn from P to the plane
) be the foot of altitude drawn from P to the plane ![]() = 0,
= 0,
![]()
![]()
Also ![]()
![]()
![]()
![]()
![]() Required distance
Required distance
![]()
![]()
Hence (C) is correct answer.
Q27. Distance of ![]() from the line
from the line ![]() is:
is:
(A)  (B)
(B) 
(C)  (D) None of these
(D) None of these
Sol. (A) Let Q(![]() ) be the foot of altitude drawn from P(
) be the foot of altitude drawn from P(![]() ) to the line =
) to the line = ![]()
![]() and
and ![]()
![]()
![]()
![]()
![]()

Q28. Let ![]() and
and ![]() be unit vector that are mutually perpendicular, then for any arbitrary
be unit vector that are mutually perpendicular, then for any arbitrary ![]() :
:
(A) ![]()
(B) ![]()
(C) ![]()
(D) None of these
Sol. Let ![]()
![]()
Also, ![]()
and ![]()
![]()
Hence (A) is correct answer.
Q29. The line ![]() will not meet the plane
will not meet the plane ![]() , provided:
, provided:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. We must have
![]() and
and ![]()
Hence (C) is correct answer.
Q30. The plane ![]() will contain the line
will contain the line ![]() , provided:
, provided:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. We must have
![]() and
and ![]()
Hence (C) is correct answer.
Q31. If the projection of point ![]() on the plane
on the plane ![]() is the point
is the point ![]() , then:
, then:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. We have
![]() and
and ![]()
![]()
![]()
Hence (B) is correct answer.
Q32. Let ![]() and
and ![]() be unit vectors that are perpendicular to each other, then
be unit vectors that are perpendicular to each other, then ![]() will always be equal to:
will always be equal to:
(A) 1 (B) Zero
(C) -1 (D) None of these
Sol. ![]()
![]()
![]()
![]()
![]()
= ![]()
Hence (A) is correct answer.
Q33. If ![]() , then the vector
, then the vector ![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
![]()
![]()
![]()
![]()
![]()
Hence (D) is correct answer.
Q34. For any two vectors ![]() and
and ![]() , the expression
, the expression ![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) Zero (D) None of these
Sol. 
![]()
Similarly, ![]()
and, ![]()
Let ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence (B) is correct answer.
Q35. Let ![]()
![]() and
and ![]() be three non zero vectors such that
be three non zero vectors such that ![]() , angle between
, angle between ![]() and
and ![]() is
is ![]() and
and ![]() is perpendicular to
is perpendicular to ![]() and
and ![]() , then
, then
 where
where ![]() is equal to:
is equal to:
(A) 1/2 (B) 1/4
(C) 1 (D) 2
Sol. 
![]()
![]()
![]()
![]()
![]()
Hence (A) is correct answer.
Q36. Let ![]() be three vectors such that
be three vectors such that ![]() ,
,![]() ,
, ![]() Then:
Then:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
![]()
![]()
![]()
![]()
![]()
Hence (A) is correct answer.
Q37. Let ![]() and
and ![]() be unit vectors such that
be unit vectors such that ![]() , then the value of
, then the value of ![]() is equal to:
is equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]()
![]()
![]()
Now, ![]()
![]()
![]()
![]()
![]()
Hence (C) is correct answer.
Q38. Let ![]() be three unit vectors such that
be three unit vectors such that ![]() If the angle between
If the angle between ![]() and
and ![]() is
is ![]() , then
, then ![]() , where
, where ![]() is equal to:
is equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) None of these
(D) None of these
Sol. ![]()
![]()
![]()
![]()
Hence (B) is correct answer.
Q39. Let P is any arbitrary point on the circumcircle of a given equilateral triangle of side length ![]() units then,
units then, ![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. Let P.V. of P, A, B and C are ![]() and
and ![]() respectively and O(
respectively and O(![]() ) be the circumcentre of the equilateral triangle ABC.
) be the circumcentre of the equilateral triangle ABC.
![]()
Now, ![]()
Similarly, ![]()
and ![]()
![]()
![]() as
as ![]()
Hence (A) is correct answer.
Q40. ![]() . A vector coplanar with
. A vector coplanar with ![]() and
and ![]() , whose projection on
, whose projection on ![]() is of magnitude
is of magnitude ![]() is:
is:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. Let the required vector be ![]()
Then, ![]() and
and ![]()
![]()
Now, ![]()
![]() (2 – 2 – 1) +
(2 – 2 – 1) + ![]() (2 – 1 – 2)
(2 – 1 – 2)
![]() or 2
or 2
If ![]() , then
, then
![]()
![]()
![]()
![]()
where ![]()
If ![]() then
then ![]()
![]()
![]()
Hence (A) is correct answer.
Q41. If am ![]() + bm
+ bm![]() + cm
+ cm![]() , m =1, 2, 3, are pairwise perpendicular unit vectors, then
, m =1, 2, 3, are pairwise perpendicular unit vectors, then  is equal to
is equal to
(A) 0 (B) 1 or –1
(C) 3 or -3 (D) 4 or –4
Sol.  =
=  =1 Þ
=1 Þ = ± 1 .
= ± 1 .
Hence (B) is correct answer.
Q42. If ![]() are three non-coplanar unit vectors, then
are three non-coplanar unit vectors, then![]() is equal to
is equal to
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol. ![]() = projection of
= projection of ![]() in the direction of
in the direction of ![]() .
.
Hence the given vector is ![]()
Hence (D) is correct answer.
Q43. If sec2A![]() and
and![]() are coplanar, then cot2A + cot2B + cot2C is
are coplanar, then cot2A + cot2B + cot2C is
(A) equal to 1 (B) equal to 2
(C) equal to 0 (D) not defined
Sol. The vectors are co-planar
Þ  = 0
= 0
Þ cot2A + cot2 B + cot2 C + 1 = 0 which is not possible.
Hence (C) is correct answer.
Q44. If a, b, c are three non - coplanar vectors and p, q, r are vectors defined by the relations ![]()
![]() r =
r = ![]() then the value of expression (a + b).p + (b + c).q + (c + a).r is equal to
then the value of expression (a + b).p + (b + c).q + (c + a).r is equal to
(A) 0 (B) 1
(C) 2 (D) 3
Sol. ![]()
Hence the given scalar expression = 1 + 1 + 1 = 3.
Hence (D) is correct answer.
Q45. The value of |a ´![]() |2 + |a ´
|2 + |a ´![]() |2 + |a ´
|2 + |a ´![]() |2
|2![]() is
is
(A) a2 (B) 2a2
(C) 3a2 (D) none of these
Sol. ![]()
Þ |a|2 sin2a + |a|2 sin2b + |a|2 sin2g
= 3|a2| – |a2|(cos2a + cos2b + cos2g)
= 2|a2| = 2a2
Hence (B) is correct answer.
Q46. If ![]() are non-coplanar vectors then
are non-coplanar vectors then  is equal to
is equal to
(A) 3 (B) 0
(B) 1 (D) none of there
Sol. ![]() = 1 – 1 = 0.
= 1 – 1 = 0.
Hence (B) is correct answer.
Q47. Consider DABC and DA1B1C1 in such a way that ![]() and M, N, M1 , N1 be the mid points of AB, BC, A1B1 and B1C1 respectively, then
and M, N, M1 , N1 be the mid points of AB, BC, A1B1 and B1C1 respectively, then
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol.
![]() Þ
Þ![]()
Þ ![]() Þ
Þ![]() Þ
Þ![]()
Þ![]() Þ
Þ![]() Þ 2
Þ 2![]()
Þ![]() Þ 2
Þ 2![]()
Þ ![]() .
.
Hence (D) is correct answer.
Q48. Let ![]() ,
, ![]() , where x1, x2, x3Î {-3, -2, -1, 0, 1, 2}. Number of possible vectors
, where x1, x2, x3Î {-3, -2, -1, 0, 1, 2}. Number of possible vectors ![]() such that
such that ![]() are mutually perpendicular, is
are mutually perpendicular, is
(A) 25 (B) 28
(C) 22 (D) none of these
Sol. ![]() Þ x1 + x2 + x3 = 0
Þ x1 + x2 + x3 = 0
Thus we have to obtain the number of integral solution of this equation.
Coefficient of x° | ( x-3 +x-2 +x-1 + x0 + x + x2)3
= x°
= x9 |(1 – x6)3 ( 1– x)-3 =11C9 – 3.5C3 = 25.
Hence (A) is correct answer.
Q49. Let a, b, c, be distinct and non-negative. If the vectors ai + aj + ck, i + k, and ci + cj + bk lie in a plane, then c is
(A) A.M. of a and b (B) G.M. of a and b
(C) H.M of a and b (D) equal to zero.
Sol.  = 0
= 0
C2® C2 – C1
–1(ab – c2) = 0 Þ c2 = ab
Hence (B) is correct answer.
Q50. If ![]() , and
, and ![]() ,then
,then ![]() is equal to
is equal to
(A) 320![]() (B) 320
(B) 320 ![]()
(C) - 320![]() (D) -320
(D) -320![]()
Sol. ![]()
![]() and process gives on
and process gives on
= –320![]() .
.
Hence (C) is correct answer.
Q51. If ![]() is the vector whose initial point divides the joining of
is the vector whose initial point divides the joining of ![]() and
and ![]() in the ratio k:1 and terminal point is origin. Also
in the ratio k:1 and terminal point is origin. Also ![]() then the interval in which k lies
then the interval in which k lies
(A) (–¥, –6] È [–1/6, ¥) (B) (–¥, –6] È [1/6, ¥)
(C) (–¥, 6] È [–1/6, ¥) (D) (¥, 6] È [–1/6, ¥)
Sol. The point that divides ![]() and
and ![]() in the ratio of k : 1 is given
in the ratio of k : 1 is given
by ![]()

Also ![]() Þ
Þ![]() Þ
Þ![]()
On squaring both sides, we get ![]()
Or 12k2 + 74k + 12 ³ 0Þ (6k + 1) (k + 6) ³ 0
![]()
Hence k Î (–¥, –6] È [–1/6, ¥).
Hence (A) is correct answer.
Q52. If 'a' is real constant and A, B, C are variable angles and, ![]() then the least value of
then the least value of ![]() is :
is :
(A) 10 (B) 11
(C) 12 (D) 13
Sol: The given relation can be re–written as
![]()
Þ ![]()
(as, a.b = |a| |b| cosq)
Þ ![]()
Þ ![]() … (i)
… (i)
also, ![]() (as,
(as, ![]() ) … (ii)
) … (ii)
from (i) and (ii), ![]()
Hence least value of ![]() .
.
Hence (C) is correct answer.
Q53. The vector ![]() and
and ![]() are collinear for
are collinear for
(A) unique value of x , 0 < x < p/6
(B) unique value of x , p/6 < x < p/3
(C) no value of x
(D) infinity many value og x, 0 < x < p/2
Sol: Since ![]() and
and ![]() are collinear, for some l, we can write
are collinear, for some l, we can write ![]() .
.
Þ ![]()
Þ ![]() Þ cosx = x
Þ cosx = x
Here we will get only one unique value of x which belongs to ![]()
Hence (B) is correct answer.
Q54. The vectors ![]() have their initial points at (1, 1), the value of l so that the vectors terminate on one straight line is
have their initial points at (1, 1), the value of l so that the vectors terminate on one straight line is
(A) 0 (B) 3
(C) 6 (D) 9
Sol: Since initial point of ![]() is
is ![]() , their terminal points will be
, their terminal points will be ![]() ,
, ![]() and
and ![]() . Now given all the vectors terminate on one straight line. Hence
. Now given all the vectors terminate on one straight line. Hence
![]() Þ l1 = 1 and l = 9
Þ l1 = 1 and l = 9
Hence (D) is correct answer.
Q55. Given that ![]() is a perpendicular to
is a perpendicular to ![]() and p is a non-zero scalar, then a vector
and p is a non-zero scalar, then a vector ![]() satisfying
satisfying![]() is given by
is given by
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) none of these
(D) none of these
Sol: We have ![]() . Taking dot by vector
. Taking dot by vector ![]() , we get
, we get
![]() Þ
Þ ![]() Þ
Þ ![]()
Þ ![]() Þ
Þ![]() .
.
Hence (A) is correct answer.
Q56. Let P is any arbitrary point on the circumcircle of a given equilateral triangle of side length '![]() ' units then
' units then ![]() is always equal to:
is always equal to:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol: Let P.V. of P, A, B and C are ![]() and
and ![]() respectively and O(
respectively and O(![]() ) be the circumcentre of the equilateral triangle ABC.
) be the circumcentre of the equilateral triangle ABC.
Þ ![]()
Now ![]()
Similarly, ![]()
and ![]()
Þ ![]() =
= ![]()
Hence (A) is correct answer.
Q57. Let ![]() and
and ![]() are two non collinear vector such that
are two non collinear vector such that ![]() . The angle of a triangle whose two sides are represented by the vector
. The angle of a triangle whose two sides are represented by the vector ![]() and
and ![]() are
are
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) none of these
(D) none of these
Sol: Let![]() , clearly
, clearly ![]() and
and ![]() are mutually perpendicular as
are mutually perpendicular as ![]() is coplanar with
is coplanar with ![]() and
and ![]() and
and ![]() is at right angle to the plane of
is at right angle to the plane of ![]() and
and ![]() . And
. And ![]()
Þ![]()
= ![]() =
= ![]()
Also, ![]() =
= ![]()
= ![]() Þ
Þ ![]()
Thus angles are ![]()
Hence (B) is correct answer.
Q58. E and F are the interior points on the sides BC and CD of a parallelogram ABCD. Let ![]() and
and ![]() . If the line EF meets the diagonal AC in G then
. If the line EF meets the diagonal AC in G then ![]() where l is equal to
where l is equal to
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Sol: (D) Let P.V. of A.B. and D be ![]() . Then
. Then ![]()
Þ ![]() and
and ![]()
Equation of EF : ![]()
Equation of AC : ![]()
For point G we must have, ![]()
Þ ![]() Þ
Þ![]()
Hence (D) is correct answer.
Q59. If  and the vector
and the vector ![]() ,
, ![]() and
and ![]() are non-coplanar, then the vectors
are non-coplanar, then the vectors ![]() and
and ![]() are:
are:
(A) coplanar (B) none coplanar
(C) collinear (D) non collinear
Sol: Given 

 [since X, Y, Z are non-coplanar]
[since X, Y, Z are non-coplanar]
Hence ![]() and
and ![]() are coplanar.
are coplanar.
Hence (A) is correct answer.
Q60. If b and c are any two perpendicular unit vectors and a is any vector, then 
(A) b (B) a
(C) c (D) b + c
Sol: Consider three non-coplanar vectors b, c and ![]() . Any vector a can be written as
. Any vector a can be written as ![]() ……(i).
……(i).
Taking dot product with ![]() in (i) we get
in (i) we get
 .Taking dot product with b in (i)
.Taking dot product with b in (i)
![]()
Taking dot product with c in (i), we get, a.c = y
Thus 
Hence (B) is correct answer.
Q61. If the lines ![]() and
and ![]() intersect (t and s are scalars) then.
intersect (t and s are scalars) then.
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) none of these
(D) none of these
Sol: For the point of intersection of the lines
![]()
Þ ![]()
Hence (B) is correct answer.
Q62. If ![]() and
and ![]() then
then
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) none of these
(D) none of these
Sol: ![]() Also
Also ![]() , and
, and ![]()
Þ ![]() are mutually perpendicular vectors.
are mutually perpendicular vectors.
Þ ![]() and
and ![]() Þ
Þ ![]()
Hence (C) is correct answer.
Q63. The position vector of a point P is ![]() where x, y, z Î N and
where x, y, z Î N and ![]() . If
. If ![]() = 10, then the number of possible positions of P is
= 10, then the number of possible positions of P is
(A) 30 (B) 72
(C) 66 (D) 9C2
Sol: Given ![]() = 10 Þ x + y + z = 10, x, y, z ³1
= 10 Þ x + y + z = 10, x, y, z ³1
The number of possible positions of P
= coefficient of x10 in (x + x2 + x3 + … )3
= coefficient of x7 in (1 – x)-3
= 3 + 7 – 1C7 = 9C7 = 9C2 = 36
Hence (D) is correct answer.
Q64. If vectors ax![]() and x
and x![]() make an acute angle with each other, for all x Î R, then a belongs to the interval
make an acute angle with each other, for all x Î R, then a belongs to the interval
(A) ![]() (B) ( 0, 1)
(B) ( 0, 1)
(C) ![]() (D)
(D) ![]()
Sol: Since vectors make an acute angle with each other so their dot product must be positive i.e. ax2 – 10 ax + 6 > 0 " x Î R
Þ- ax2 + 10ax – 6 < 0 " x Î R Þ –a < 0 and 100a2< 24a
Hence (C) is correct answer.
To read more, Buy study materials of Vectors comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.
View courses by askIITians


Design classes One-on-One in your own way with Top IITians/Medical Professionals
Click Here Know More

Complete Self Study Package designed by Industry Leading Experts
Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child
Click Here Know More