Introduction of Vectors
Table of Content |
Vectors is an important topic in the mathematics syllabus of JEE. This chapter includes various topics like Vectors and Scalars, addition of vectors, components of a vector in two dimensions and three dimensional space, scalar and vector products, scalar and vector triple product, Application of vectors to plane geometry. We start with the introduction of vectors.
Introduction
A vector is a quantity which has both the magnitude and the direction. Geometrically a vector is represented by a directed line segment as shown in the adjacent figure or it may be denoted by boldfaced letters. The direction is indicated by the length of the segment AB. A is called the initial point and B the terminal point of vector AB = a.
The line l, of which the segment AB is a part, is called the line of support. The length is denoted by |AB|= |a| = AB= a.
A scalar is a quantity that has only the magnitude and no direction. In other words, a scalar is just a real number.
Displacement, velocity, momentum, area are some examples of vectors while distance, speed, volume temperature are just scalars.
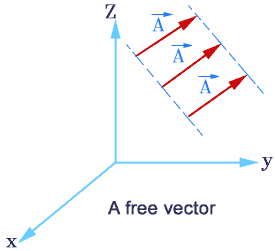
Free Vectors
A vector that can be displaced parallel to itself and applied at any point is known as a Free Vectors. A free vector can be specified by giving its magnitude and any two of the angles between the vector and coordinate axes. Hence free vectors are the vectors in which only the magnitude and the direction are specified but no line of action or position is specified. The vectors which are characterized by the magnitude, direction as well as line of action are called line or bound vectors.
Displacement, velocity are free vectors while force and moment of a force about a point are line vectors.
Null Vector: A null vector is a vector of zero magnitude and arbitrary direction. When a vector is added to its own negative vector, the resultant is the null vector
It is represented by 0. A null vector has no direction or it may have any direction. Generally a null vector is either equal to resultant of two equal vectors acting in opposite directions or multiple vectors in different directions.
0 = A + (-A)
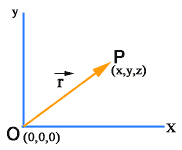
Position Vector of a Point
A vector that indicates the position of a point in a coordinate system is referred to as the Position Vector.
Suppose we have a fixed reference point O, then we can specify the position of a given point P with respect to point O by means of a vector having magnitude and direction represented by a directed line segment OP .This vector is called Position Vector.
In a three dimensional coordinate system if O is at origin then O (0,0,0) and P is any point say P(x,y,z)
in this situation position vector of point P will be:
r = xi + yj + zk, where i, j and k denote the unit vectors in the directions of x, y and z axis respectively.
Watch this Video for more reference
Angle Between Two Vectors
Angle between two vectors is defined as the smaller of the angles formed when the initial points or the terminal points of two vectors are brought together.
Dot Product of Two Vectors: The dot product of two vectors
a = [a1, a2, ..., an] and b = [b1, b2, ..., bn] is defined as
where Σ denotes summation notation and n is the dimension of the vector space. For instance, in three-dimensional space, the dot product of vectors [1, 3, −5] and [4, −2, −1] is:
[1,3,-5] . [4,-2,-1] = (1) (4) +(3) (-2) +(-5) (-1)
= 4-6+5=3
Geometrically, the dot product between two vectors a and b is defined as
a.b = ||a|| ||b|| cos θ, where θ is the angle between a and b.
In particular, if a and b are orthogonal, then the angle between them is 90° and
Moreover, the dot product of a vector by itself is
a.a = ||a||2.
You may also refer the Sample Papers to get an idea about the types of questions asked.
Multiplication of a Vector by a Scalar
Given a vector a and a scalar k ∈ R, then k a (or ak) denotes a vector whose magnitude is |k| a i.e., k times that of a and whose direction is the same or opposite to that of a according as k > 0 or k < 0 respectively. Also, 0 a = 0, zero or null vector which has zero magnitude and arbitrary direction.
1 a = a, (-1) a = - a, etc.
When we have two vectors a and b such that b = k a, k ∈ R, then a and b are called collinear vectors. b is said to be a scalar multiple of a.
a and b are parallel if k > 0 and anti parallel if k < 0.
Note also that k1 (k2 a) = (k1k2) a = k2(k1 a), where k1, k2 ∈ R.
A vector having the magnitude as one (unity) is called a unit vector.
To read more, Buy study materials of Vectors comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.