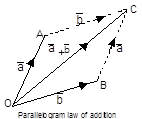Adition of Two Vectors
Table of Content |
A vector has magnitude and direction. So when two vectors are added both the magnitude and direction are taken into consideration.
Triangle Law of Addition
Given two vectors a and b, their sum or resultant written as (a+b) is also a vector obtained by first bringing the initial point of b to the terminal point of a and then joining the initial point of a to the terminal point of b giving a consistent direction by completing the triangle OAB.
And here is how to add two vectors after breaking them into x and y parts:
The vector (8, 13) and the vector (26, 7) add up to the vector (34, 20)
Example: Add the vectors a = (8, 13) and b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
Parallelogram Law of Addition
|
The sum can also be obtained by bringing the initial points of a and b together and then completing the parallelogram OACB
|
|
Also, a + ( b + c ) = (a + b) + c i.e. the addition of vectors obeys the associative law. If a and b are collinear, their sum is still obtained in the same manner although we do not have a triangle or a parallelogram in this case.
Polygon Law of Addition
|
For adding more than two vectors, we have a polygon law of addition which is just an extension of the triangle law. OA + AB + BC+ CD + DE + EF= OF A consequence of this is that, if the terminus of the last vector coincides with the initial point of the first vector, the sum of the vectors is 0 vector. To obtain a-b (difference of two vectors), perform addition of a and (-b). (k1 + k2) a = k1a + k2a ; k (a + b) = ka + kb. |
|
You may refer the Sample Papers to get an idea about the type of questions asked .
Properties of Vector Addition
Certain Rules to be followed while Adding Two Vectors
-
Vectors in the same direction can be added by simply adding their magnitudes. But if the vectors to be added are in opposite directions, then their magnitudes are subtracted and not added.
-
Vectors represented in the form xi + yj + zk can be added by simply adding the coefficients of the three unit vectors. The answer will also be in i,j,k form.
-
Column vectors can be added by simply adding the values in each row.
-
You can find the magnitude of a vector in three dimensions by using the formula a2=b2+c2+d2, where a is the magnitude of the vector, and b, c, and d are the components in each direction.
-
Vectors should not be confused with magnitudes.
Illustration : ABCD is a parallelogram A1 and B1 are the midpoints of side BC and CD respectively. If AA1 + AB1= µAC then find the value of µ.
Key concept: In such type of questions related to parallelogram or triangle first we define the origin and position vector of different vertices.
Solution: Let P.V. of A, B, D be 0, b and d respectively. Then P.V. of C = b+d.
Also P.V. of A1= b+d/2 and P.V. of B1= d+b/2
AA1 + AB1= 3/2(b +d) = 3/2 AC
Hence the value of µ is 3/2.
Illustration : In a quadrilateral PQRS, PQ = a, QR = b, SP = a-b, M is the midpoint of QR and X is a point on SM such that SX = 4/5 SM, then prove that P, X and R are collinear.
Solution: From the given information, we get QM = b/2 and hence PM = a+b/2
Also, SM = PM- PS= 2a-b/2 and SX= 4/5 SM = 8/5 a – 2/5 b
PX= PS+SX = -a+b+(8/5)a-(2/5)b=3/5(a+b)
PR= PQ+QR = a+b
PX/PR = 3/5
Hence, P, X and R are collinear.
Illustration : The points with position vectors
60i + 3j, 40i -8j, ai – 52j are collinear if
1. a = - 40 2. a = 40
3. a = 20 4. None of these
Solution: It is given that the three points A, B and C are collinear
If AB = -20i -11j and AC = (a-60)i -55j, then AB || AC.
This means that (a-60)/-20 = -55/-11
Hence, a = -40.
Illustration : Let a, b, c be three non-coplanar vectors and p, q, r are vectors defined by the relations
p = b x c/ [a b c], q = c x a/ [a b c], r = a x b/ [a b c],
then what is the value of the expression
(a + b) p + (b + c) q + (c + a) r?
Solution: Given expression is
∑ (a + b). (b x c)/ [a b c]
= ∑ ({[a b c] + [b b c]}/ [a b c])
= ∑ (1 + 0) = 3. (If a vector repeats itself in a scalar triple product, its value is 0).
Illustration : Let A, B and C be vectors of length 3, 4, 5 respectively. Let A be perpendicular to B + C, B to C + A and C to A + B. then find the length of the vector A + B + C?
Solution: Given that |A| = 3, |B| = 4 and |C| = 5
Since, A.(B + C) = B.(C + A) = C. (A + B) ….. (1)
Hence, | A + B + C |2 = |A|2 + |B|2 + |C|2 + 2 (A.B + B.C + C.A)
= 9 + 16 + 25 + 0
A.B + B.C + C.A = 0….. (follows from eq (1))
Therefore, | A + B + C |2 = 50
Hence, | A + B + C | = 5√2
Watch this Video for more reference
To read more, Buy study materials of Vectors comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.