Slope of a Line

Define Straight Line in brief

Straight Line is the locus of a moving point P (h, k), which moves in such a condition that P is always collinear with the given two fixed points.

Also, we know from the concept of collinearity that, three points are collinear if they lie on a same straight line or the area of triangle from by these points is zero.

Examples

y = 5, 2x + 5y + 3 = 0, x = 2y – 5 are few examples of straight lines, but y = log(x), y = x², y = x + 1/x does not represent straight lines.

In this article, we will be discussing about straight lines in two variables only. The general equation of straight line in two variables is represented as:

ax + by + c = 0

Where, a and b are the coefficients of x and y respectively and c is called as the Constant.

What is the slope in math?

If we plot a straight line on a Cartesian (XY) plane, then we can see the inclination of the straight line with respect to the x – axis. This inclination or the angle between the straight line and the positive x – axis is termed as slope of a line.

In the Image above, we can observe different lines passing through same point (origin) but have different inclinations with the x – axis. This inclination is termed as the slope of the line.

Given a point, we can have infinite number of straight lines passing through it. This suggest us to have another condition for the same line to be uniquely represented on the XY plane. 

Example

A straight line passing through the origin and having the slope of 90^° or 270°  or – 90^° is the y – axis itself.

From the above example, we can learn two more points:

• For any specific line, if the slope is θ, then it will also have the slope of nπ + θ,  where n is any positive integer.

• The angle measured in anti-clock wise direction is taken as positive while the angle in clock wise direction is considered as negative.

If the inclination of any line from the positive x – axis is θ, then its slope is given by tan θ and is generally represented by m. Slope is also called as the Gradient.

Thus,

Note:- θ can only lie in [0,180^°) or (-180°, 0].

Assume, two given points A (x₁, y₁) and B(x₂, y₂) given in the figure and a line passing through these points. As per the definition of slope, we can write

Can Slope be negative?

Since the slope is very important parameter in the straight line, we must take care of its all the important points.

• Since the slope = tan θ (considering the θ to be positive that is, angle is measured in the anti-clock wise direction) and thus the slope can positive or negative depending upon the quadrant of angle.

As we know from the basic trigonometry that the tan θ is positive in first and the third quadrant. While it is negative in second and fourth quadrant. Thus, on the basis of this, we may say:

1. If 0 < θ < 90°

Slope will be positive as tan θ is positve

2. If 90° < θ < 180° 

Slope will be negative as tan θ is negative

• If θ, which means the inclination towards x – axis is zero. This will represent a straight line parallel to x – axis.

Whereas, if θ = 90°, then the line will be perpendicular to x -axis or parallel to the y – axis.

• For the Points A(x₁, y₁) and B(x₂, y₂), the slope will calculated as: 

Thus, from the above points, we can define the slope as a number which represents steepness and the direction.

By the direction here means, increasing or decreasing. If the slope is positive, then the line will be increasing while travelling from left to right on the x - axis, whereas for positive slope, line decreases while travelling from right to left direction.

The absolute value or the magnitude of slope represents the steepness of the line. Greater the absolute value steeper is the line.
 

How do you change an equation into slope intercept form?

Straight Lines can be represented into different forms depending upon the type of information available with us for a line. These forms are as follows:

• General form

• Point - slope form

• Two - point form

• Slope – intercept form

• Intercept – form

• Normal form or perpendicular form

Given the equation in any form, we can easily convert it into any other desired form. Let’s take a general form of a straight line and we will try to change it into the slope intercept form.

So, we have

L: ax + by + c = 0  ……………….. (1)

Follow the below steps to convert any equation into slope intercept form:

Step 1) Divide the given equation by the coefficient of y so as to make it equals to 1.

On dividing equation (1) by b, we get

(a/b)x + y + (c/b) = 0

Step 2) Keep y on one side (RHS) and bring all other terms on the other side

y = -(a/b)x – (c/b)

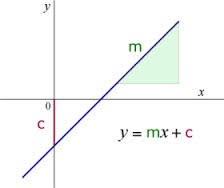*Note:- Keep the sign of y as positive.

Obtained equation is in slope intercept form. The general equation in slope intercept form is as: y = mx + C. Now compare the obtained equation with this general equation to get the value of slope and y – intercept.

m = -(a/b) and C = -(c/b)

Example

Convert 2x – 4y -16 = 0 into the slope intercept form

Dividing the given equation by 4, we get

0.5x – y – 4 = 0,

on rearranging we get

y = 0.5x – 4

How do you find the slope of a line from an equation?

Any equation if converted into slope - intercept form, then its slope can be easily obtained. So, given the equation, first convert it into slope – intercept form by the method as explained in the previous heading. Then by comparing the obtained equation with the general equation of slope – intercept form, slope can be obtained.

Example

What is the slope of the line represented as y = -3x + 5

As the given equation is already in slope intercept form, so we can directly say,

slope = m = -3

Example

Find the slope of the line represented as 24x - 6y = 12

Dividing the given equation by 6,

4x – y = 2

rearranging in the slope – intercept form,

y = 4x – 2

On comparing, we get slope = 4.

Here, the value of slope = 4 represents, that with the increase in one unit of x, y increases by four times. 

More Readings

Slope of a Lin