General Equation of a Line
Table of Content |
Who is the founder of Linear Equation?
Linear Equations were invented by Irish mathematician, physicist and astronomer Sir William Rowan Hamilton in 1843. Sir Hamilton have made the great contributions in field of mathematics.
He has made the special contribution in the algebra by inventing the linear equation. His main work was in the field of mathematical physics and thus the application of his work can be found in various fields in physics like quantum mechanics.
What is the definition of Linear Equation in math?
The word ‘Linear equation‘ is made up of two different words linear and equation. Linear means an algebraic expression having its degree (the highest power on the variable) as one. While, if any algebraic expression equated to zero or any other constant or expression becomes an equation.
Example
f(x) = 2x + 3y – 2z, g(x) = 2x – 1, h(x) = x – 3y + 2 are the examples of linear algebraic equation as the highest power of any variable is equals to one.
If the above linear expressions are equated to zero, then it becomes a linear equation.
that is,
also,
g(x) = 0 ⇒ 2x – 1 = 0
and
h(x) = 0 ⇒ x – 3y + 2
How do you describe a Linear Equation?
As explained above, linear equation is any algebraic equation having degree as one and is equated to zero.
In general, any linear equation having n different variables can be expressed as:
a1x1 + a2x2 + a3x3 + a4x4 + …………………….. + anxn + c = 0
where, a1, a2 ,.. an are the coefficients of x1 , x2 , .. xn respectively and c is any constant.
A linear equation in n variables can represents different graphical shapes.
Example
x = 2 is a one dimension straight line, 2x + 3y = 1 is a two dimension straight line, but x – 7y + 10 = 0 represents the equation of the plane in three dimension and so on.
Below are few graphical examples of one, two and three-dimensional equation of line.
What is a Linear Equation in two variables?
The general equation of a straight line in two variables can be represented as:
ax + by + c = 0
Where, a and b are the coefficients of x and y respectively and c is any arbitrary constant.
The reason, why we call the above linear equation in two variables as a straight line because when this equation is represented on the graph, it will be drawn as Straight Line.
Let us take one example and try to plot its graph.
Example
y = 2x + 3
To plot the graph, we usually keep one variable on Right hand side and take other variables and constant on left hand side.
Now look for the vales of y for different vales of x.
For x = 0, we get y = 3
For x = 1, we get y = 5
For x = 2, we get y = 7
For x = 3, we get y = 9
For x = -1, we get y = 1
For x = -2, we get y = -1
We can also arrange these values in tabular form.
| X | -2 | -1 | 0 | 1 | 2 | 3 |
| Y | -1 | 1 | 3 | 5 | 7 | 9 |
Now mark the above co-ordinates on a XY – plane. After joining these points, we will get the straight line as shown in the graph below:
What is C in the general form of a line?
The general form of a line is given by:
y = mx + c
Where, m is the slope and c represents the y – intercept of the equation of line.
y – intercept is an ordinate of a point on the y – axis where the line intersects with the y – axis. y – intercept can also be defined as the length of the line segment between the origin and the point where line intersects with y – axis.
The value of c can be positive, negative or even zero.
- If C is positive that is, C > 0
In y = mx + c, if c is positive that means for x = 0, the value of y = c which will always be positive.
Thus, the graph of a line at x = 0 will always be above the x – axis.
- If C is negative that is, C < 0
In y = mx + c, if c is negative that means for x = 0, the value of y = c which will again always be negative.
Thus, the graph of a line at x = 0 will always be below the x – axis.
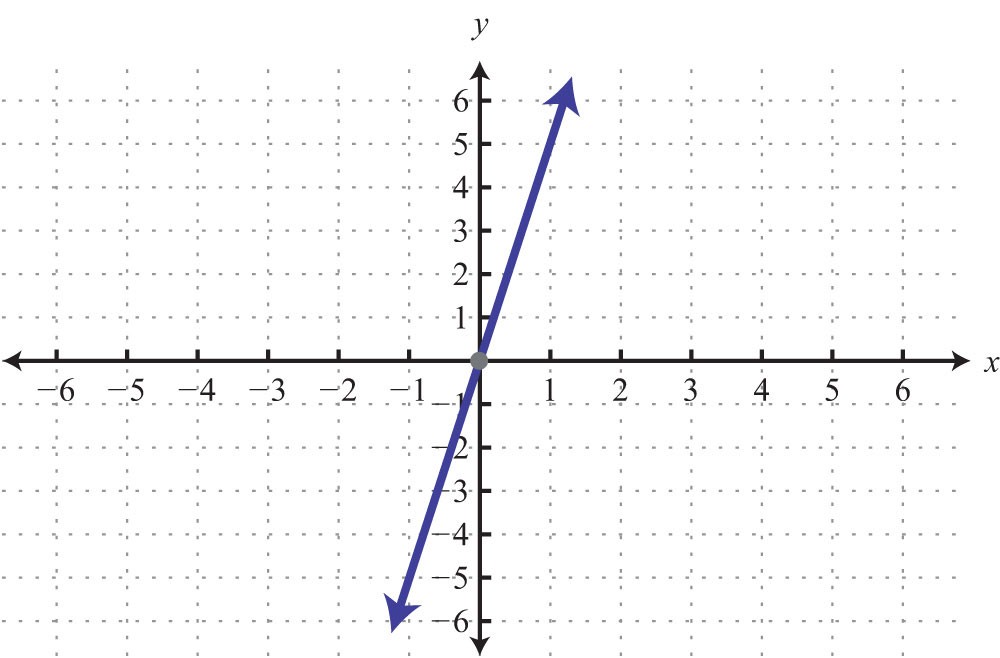
- If C is zero that is, C = 0
In y = mx + c, if c is zero that means for x = 0, the value of y = c will also be zero. That means the point (0, 0) will always satisfy the equation.
Thus, the graph of a line will always pass through origin.
How the linear equations can be represented in matrix form?
Matrix is an array of numbers represented as follows:
So, we can also represent a linear equation in the matrix form.
For ax + by + cz = 0, its matrix representation will be as
For solving the linear equations, we need as many number of different equations as the variables in the equation. For example, for two variable equations we need two equations. Similarly, for three variable equations, we need three equations and so on.
Thus, for solving the below equations:
2x + y + 3z = 4
x – y + 10z = -3
20x + 2y – 13z = 0
We can form a matrix as:
Then this can be solved using one of the matrix method to get the values of x, y and z.
More Readings