Family of Lines

Straight lines is an important topic of mathematics syllabus of IIT JEE. The topic is quite vast and requires thorough understanding of the concepts. When we talk of straight lines, other topics that come to our mind are pair of straight lines and family of lines. This section stresses on these topics in detail. 

Before we proceed toward family of straight lines we shall first discuss pair of straight lines and the joint equation of pair of straight lines. 

Now, we throw some light on the General Equation of Second Degree representing a Pair of Straight Lines

The equation ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents a second degree equation where a, h, b don’t vanish simultaneously.

Let a ≠ 0.

Now, the above equation becomes

a²x² + 2ax (hy + g) = aby² – 2afy – ac

On completing the square on the left side, we get,

a²x² + 2ax (hy + g) = y²(h² – ab) + 2y(gh – af) + g² – ac.

i.e. (ax + hy + g) = + √y²(h²–ab) + 2y(gh–af)g² – ac

We cannot obtain x in terms of y, involving only terms of the first degree, unless the quantity under the radical sign be a perfect square. The condition for this is,

(gh – af)² = (h² – ab) (g² – ac)

i.e. g²h² – 2afgh + a²f² = g²h² – abg² – abg² – ach² + a²bc

Cancelling and dividing by a, we have the required condition as

abc + 2fgh – af² – bg² – ch² = 0

Note:

The angle α between two lines represented by the general equation is the same as the one represented by its homogeneous part.

Illustration 1:

What is the point of intersection of two straight lines given by general equation ax² + 2hxy + by² + 2gx + 2fy + c = 0?

Solution:

The general solution is

ax² + 2hxy + by² + 2gx + 2fy + c = 0                   …… (1)

Let (α, ß) be the point of intersection we consider line paralleled transformation.

x = x’ + α,         y = y’ + ß

From (1) we have

a(x’ + α)² + 2h(x’ + α) (y’ + ß) + b(y’ + ß)² + 2g(x’ + α) + 2f(y’ + ß) + c = 0

⇒ ax’² + 2hx’y’ + by’² + aα² + 2hαß + bß² + 2gα + 2fß + 2x’(a α + hß + g) + 2y’ + 2y’ (hα + bß + f) = 0

⇒ ax’² + 2hx’y’ + by’² + 2x’(aα + hß + g) + 2g’ + 2y’ (hα + bß + f) = 0

Which must be in the form ax'² + 2hx’y’ + by’ = 0

This cannot be possible unless aα + hß + g = 0

hα + bß + f = 0

Solving α/hf–bg = ß/hg–af = 1/ab–h²

α = hf–bg/ab–b², ß = hg–af/ab–h²

Illustration 2:

Represent lines parallel to y = 2x and y = 3x by a second degree equation

Solution:

The lines parallel to y = 2x and y = 3x can be represented as

(y – 2x – c₁) (y – 3x – c₂) (where c₁ and c₂ are constants)

This gives 6x² – 5xy + y² + (3c₁ + 2c₂) x + (– c₁ – c₂) y + c₁ c₂ = 0

Note:

1. Homogeneous part is same as for the equation of above illustration. Therefore, the homogeneous part of a general second degree equation determines the slope of the lines i.e. lines parallel to ax² + 2hxy + by² + c = 0 and through the origin are represented by the equation ax² + 2hxy + by² = 0

2. The equation ax² + 2hxy + by² + 2fy + c = 0 represents a pair of parallel straight lines if h/a = b/h = f/g or bg² = af²

The distance between them is given by 2√g²–ac/a(a+b) or √f²–bc/b(a+b).

Illustration 3:

Does the second degree equation x² + 3xy + 2y² – x – 4y – 6 = 0 represent a pair of lines? If yes, find their point of intersection.

Solution:

We observe that a = 1, h = 3/2, b = 2, g = –1/2, f = 2, c = – 6

abc + 2fgh – af² – bg² – ch² = – 12 + 3 – 4 – 1/2 + 27/2 = 0

Therefore the given second-degree equation represents a pair of lines, x² + 3xy + 2y² – x – 4y – 6 = (x + 2y + 2) (x + y – 3).

Consider the equations formed by first two rows of 

.

i.e. ax + hy + g = 0 and hx + by + f = 0

i.e. x + 3/2 y – 1/2 and 3/2 x + 2y – 2 = 0

Solving these, we get the required point of intersection.

i.e. 2x + 3y – 1 = 0

3x – 4y – 4 = 0

Solving the above equation, we get x = 8, y = –5.
 

What do you mean by the joint equation of a pair of Straight Lines?

If the line lx + my + n = 0, (n ≠ 0) i.e. the line not passing through origin) cuts the curve ax² + by² + 2gx + 2fy + c = 0 at two points A and B, then the joint equation of straight lines passing through A and B and the origin is given by homogenizing the equation of the curve by the equation of the line. i.e. if we have a line lx + my + n = 0 and a second degree curve given by the equation ax² + 2hxy + by² + 2gx + 2fy + c = 0, then the joint equation of a pair of straight lines joining origin to the points of intersection of both is given by  

ax² + 2hxy + by² + (2gx + 2fy) (lx+my/–n) + c (lx+my/–n)² = 0. This is the equation of the lines OA and OB.

Illustration 1:

Prove that the straight lines joining the origin to the points of intersection of the straight line hx + ky = 2hk and the curve (x – k)² + (y – y)² = c² are at right angles if h² + k² = c².

Solution:

Making the equation of the curve homogeneous with the help of that of the line, we get

x² + y² –2(kx + hy) (hx+ky/2hk) + (h² + k² – c²) (hx+ky/2hk) = 0

or 4h²k²x² + 4h²k²y² – 4h²x(hx+ky) – 4h²ky(hx + ky) + (h² + k² – c)(h²x² + k²y² + 2hxy) = 0.

This is the equation of the pair of lines joining the origin to the points of intersection of the given line and the curve. They will be at right angles if

Coefficient of x² + coefficient of y² = 0 i.e.

(h² + k²) (h² + k² – c²) = 0 ⇒ h² + k² = c²       (since h² + k² ≠ 0).
 

What is family of lines?

Having studied pair of lines and the joint equation of pair of lines, we now proceed toward the family of lines. The general equation of the family of lines through the point of intersection of two given lines is L + λL’ = 0, where L = 0 and L’ = 0 are the two given lines, and λ is a parameter.

Remark:

1. Conversely, a line of the form L₁ + λL₂ = 0 passes through the point which is the point of intersection of the lines L₁ = 0 and L₂ = 0. 

2. This also implies that if a linear expression contains an undetermined coefficient then that represents a family of straight lines. Note that in this case, the line L= 0 cannot be a fixed line.

3. If the lines L₁ and L₂ are parallel lines then they meet at infinity.

4. If we have a line ax + by + c = 0, then the line perpendicular to this line is given by bx - ay + k = 0, where k is a parameter.

5. If we have a line ax + by + c = 0, then the line parallel to this line is given by ax + by + k = 0, where k is a parameter.

Illustration 1:

A variable line through the point of intersection of the lines x/a + y/b = 1 and x/b + y/a = 1 meets the coordinate axes in A and B. Show that the locus of the midpoint of AB is the curve 2xy(a + b) = ab(x + y).

Solution:

Let (h, k) be the midpoint of the variable line AB.

The equation of the variable line AB is (bx + ay – ab) + λ(ax + by – ab) = 0

Coordinates of A are (ab(1+λ)b + λa).

Coordinate of B are (0, ab(1+λ)b + λa).

Mid-point of AB is (ab(1 + λ)2(b + λa), ab(1 + λ)2(a + λb))

⇒ h = ab(1+λ)2(b+λa); k = ab(1+λ)2(a+λb) 

⇒ 1/2h = b+λa/ab(1+λ); 1/2k = a+λb/ab(1+λ)

⇒ 1/2h + 1/2k = a+b/ab ⇒ (h + k)ab = 2hk (a + b).

Hence the locus of the midpoint of AB is (x + y) ab = 2xy (a + b).

To find the equation to the straight lines which pass through a given point (x₁, y₁) and make equal angles with the given straight line y = m₁x + c.

If m is the slope of the required line and α is the angle which this line makes with the given line, then tan a = + (m₁–m)/(1+m₁m).

1. The above expression for tan α, gives two values of m, say m_A and m_B.

Illustration 1:

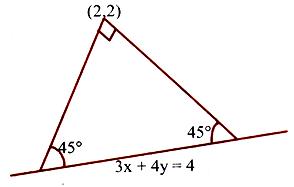
Find the equations to the sides of an isosceles right-angled triangle, the equation of whose hypotenuse is 3x + 4y = 4 and the opposite vertex is the point (2, 2).

Solution:

The problem can be restated as:

Find the equations to the straight lines passing through the given point (2, 2) and making equal angles of 45^o with the given straight line 3x + 4y – 4 = 0

Slope of the line 3x + 4y – 4 = 0 is m₁ = –3/4

Illustration 2:

The straight lines 3x + 4y = 5 and 4x – 3y = 15 intersect at the point A. On these lines points B and C are chosen so that AB = AC. Find the possible equations of the line BC passing through (1, 2).

Solution:

The two given straight lines are at right angles.

Since AB = AC, the triangle is an isosceles right angled triangle.

The required equation is of the form y – 2 = m(x – 1)              … (1)

with tan 45^o = + m+3/4/1–3m/4 = + m–4/3/1+4m/3

⇒ 1 = + m+3/4/1–3m/4 = + m–4/3/1+4m/3 ⇒ m = – 7, 1/7.

Substitute the value of m in (1). We get the required equations.

Illustration 3:

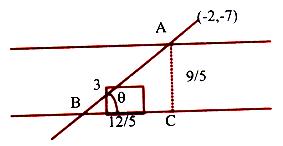
Find the equation of the straight line passing through (–2, 7) and having intercept of length 3 units between the straight lines 4x + 3y = 12 and 4x + 3y = 3.

Solution:

Distance AC between the two given parallel lines

= |c₁–c₂/√a² + b²| = 12–3/√(16 + 9) = 9/5.

⇒ BC = 12/5. If θ is the angle between BC and AB, then tan θ = 9/12 = 3/4.

Slope of the parallel lines = –4/3 = m₂.

If m₁ is the slope of the required line, then tan θ = m₁–m/1+m₁m ⇒ 3/4 = + m₁–4/3/1+4/3m₁

i.e. m₁ + 4/3 = 3/4 (1 – 4/3 m₁) and m₁ + 4/3 = 3/4 (1 – 4/3 m₁).

The slopes are (i) m₁ = –7/24 (ii) m₁ = ∞ (the line is parallel to the y-axis).

The required equations of the lines are 7x + 24y + 182 = 0 and x + 2 = 0.

Alternative Solution:

Equation of the line, through P(–2, 7) and making angle θ with the x-axis, is x+2/cosθ = y+7/sin θ = r.

If this line intersects the given lines at A and B, with AB = 3, the points A and B are A(–2 + r₁ cos θ, – 7 + r₁ sin θ) and B (–2 + (r₁ + 3) cos θ, – 7 + (r₁ + 3) sin θ).

Since A and B lie on the lines 4x + 3y = 3 and 4x + 3y = 12, we have

4r₁ cos θ + 3r₁ sin θ = 32 and

4r₁ cos θ + 3r₁ sin θ + 12 cos θ + 9 sin θ = 41, so that

12 cos θ + 9 sin θ = 0 or 4 cos θ + 3 sin θ = 3.

Solving this equation we find that θ = π/2 and tan θ = –7/24.

Hence the required lines are x + 2 = 0 and y + 7 = –7/24 (x + 2) i.e. 7x + 24y + 182 = 0.
 

Related Resources

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.