Examples based on Straight Line
 Straight Lines is an important topic of coordinate geometry. Various competitive exams like the JEE usually ask several questions from this topic. Students planning to take such elite exams must try to cover all possible topics of IIT JEE Mathematics including straight lines in order to remain competitive in the JEE.
Straight Lines is an important topic of coordinate geometry. Various competitive exams like the JEE usually ask several questions from this topic. Students planning to take such elite exams must try to cover all possible topics of IIT JEE Mathematics including straight lines in order to remain competitive in the JEE.
Illustration 1:
Reduce 3x – 4y + 5 = 0 to all other forms.
Slope Intercept Form
y = 3/4 x + 5/4
where, m = slope = 3/4
c = 5/4 (y – intercept)
Intercept Form
We can write the given line as 3x – 4y = –5
⇒ 3x/–5 + 4y/5 = 1
x/–5/3 + y/5/4 = 1 (intercept form)
x – intercept = –5/3
y – intercept = 5/4
Point – Slope Form
Let x = 1, then y = 3/4 + 5/4 = 2
y – 2 = 3/4 (x – 1)
Parametric Form
x–1/cos θ = r, where tan θ = 3/4
⇒ x–1/4/5 = y–2/3/5 = r
Normal Form
3x – 4y = – 5
–3x + 4y = 5
Dividing by ((–3)2 + 4)½
⇒ –3/5 x + 4/5 y = 5/5 = 1
⇒ x cos α + y sin α = p, p > 0
Where cos α = –3/5, sin α = 4/5, p = 1
___________________________________________________
Illustration 2:
The straight line drawn through the point P(0, 3) and making an angle of 30o with positive x-axis, meets the line x + y = 6 at Q. Find the length PQ.
Solution:
We can solve the question by two methods. We illustrate here both the methods one by one:
Method 1.
Equation of the line through the point P is
(x–0)/cos 30 = (y – 3)/sin 30 = r
⇒ xQ = √3/r , yQ = 3 + r/2, r = distance PQ
Point Q lies on x + y = 6 and hence we have
⇒ r√3/2 + (3 + r/2) = 6
⇒ r = 6/√3+1
Method 2.
Equation of the line through the point P is y = 1/√3 x + 3 [because here m = tan 30o = –1/√3, c = 3]
Solving this line, with x + y = 6, we get
xQ = 3√3/√3+1, yQ = 3√3+6/√3+1
distance PQ = √(xQ – xP)2 + (yQ – yP)2
= 6/√3+1
_________________________________________________________________________
Illustration 3:
Find the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with positive direction of x-axis is 15o.
Solution:
Here, we are given p = 4 and ω = 15o.
Now cos 15o = √3+1/2√2
and sin 15o = √3–1/2√2
By the normal form, the equation of the line is
x cos 15o + y sin 15o = 4 or √3+1/2√2 x + √3–1/2√2 y = 4
or (√3 + 1) x + (√3 – 1)y = 8√2.
This is the required equation.
_____________________________________________________________________
Illustration 4:
Find the equation to the straight line which passes through the point (–5, 4) and is such that the position of it between the axes is divided by the given point in the ratio 1 : 2.
Solution:
Let the required straight line be (x/a) + (y/b) = 1.
Using the given conditions, P (2a+1.0/2+1, 2.0+1.b/2+1) is the point which divides (a, 0) and (0, b) internally in the ratio 1 : 2.
But the point P is (–5/4)
Hence –5 = 2a/3, 4 = b/3 ⇒ a = –15/2, b = 12.
Hence the required equation is x/(–15/2) + y/2 < θ < π.
⇒ tan θ = –√8 = slope of line.
We know that the equation of the straight line passing through the point (x1, y1) having slope m is y – y1 = m(x – x1).
Therefore the equation of the required line is y – 2 = –√8 (x – 1)
⇒ √8 x + y – √8 – 2 = 0.
_______________________________________________________________________
Illustration 5:
Find the equation of the line joining the points (–1, 3) and (4, –2).
Solution:
Equation of the line passing through the points (x1, y1) and (x2, y2) is
y – y1 = y1–y2/x1–x2 (x – x1)
Hence equation of the required line will be
y – 3 = 3+2/–1–4 (x + 1) ∝ x + y – 2 = 0.
_______________________________________________________________________
Illustration 6:
It is possible to find the distance of of a point form a line but how can we determine as to which side of the line does the point lie?
Solution:
From the figure, we observe that
ax0 + by0 + c = 0 (Since the point (x0, y0) lies on the line) …… (1)
Consider, ax1 + by1 + c
= (ax0 + c) + by1 [x0 = x1 = x2]
= b(y1 – y0)
= –ve
Consider, ax2 + by2 + c
= (ax0 + c) + by2
= b(y2 – y0)
= +ve
Thus we observe that the point is on one side of the line, if put in the expression of line is gives one sign, while the point is on the other side of the line, if put in the expression of line it gives opposite sign.
__________________________________________________________________________________
Illustration 7:
Represent the straight-line y = x + 2 in the parametric form.
Solution:
Slope of the given line is = 1 = tan π/4.
Equation of the straight line can be written as y – 2 = x.
or y–2/1/√2 = x/1/√2= r.
Any point on the line is (r/√2, 2 + r/√2).
The point (x, y) is at a distance r from the point (0, 2).
________________________________________________________________________________
Illustration 8:
Tangents are drawn from the point P(3, 4) to the ellipse x2/9 + y2/4 = 1 touching the ellipse at the points A and B. The equation of the locus of the point whose distances from the point P and the line AB are equal is...? (IIT JEE 2010)
Solution:
Clearly, the moving point traces a parabola with focus at P(3, 4) and directrix as AB:
(y-0)/(x-3) = -1/3 or x+3y -3 = 0
Hence, the equation of parabola is
(x-3)2 + (y-4)2 = (x+3y-3)2/10
Hence, the required equation is
9x2 + y2 – 6xy – 54x – 62y + 241 = 0.
____________________________________________________________________________
Illustration 9:
A straight line moves so that the sum of the reciprocals of its intercepts on the coordinate axis is constant. Show that it passes through a fixed point.
Solution:
Let the variable line be x/a + y/b = 1.
Then, we are given in the question that 1/a + 1/b = K, where K is a constant.
Hence, the variable line takes the form
x/a + (K-1/a)y – 1 = 0
or 1/a(x-y) + (Ky-1) = 0
This clearly represents a straight line through the intersection of x-y = 0 and Ky – 1 = 0.
The lines intersect at (1/K, 1/K) and hence x/a + y/b = 1 always passes through the fixed point (1/K, 1/K).
_________________________________________________________________________________
Illustration 10:
Find the acute angle between the lines
2x + y + 11 = 0, x – 6y + 7 = 0.
Solution:
The gradients of the above lines are -2 and 1/6.
Also, the angle of slope of the first line is in second quadrant while that of second line is in first quadrant. Hence, we have
m2 = -2, m1 = 1/6 and tan θ = (-2-1/6)/(1 + (-2)(1/6)) = -13/4
This shows that θ is an obtuse angle.
If φ is the acute angle between the lines, then θ = 180o – φ
and so we have, tan θ = tan (180o – φ).
But, tan (180o – φ) = – tan φ and so
tan θ = – tan φ
So, we have tan φ = - tan θ = -(-13/4) = 13/4.
_______________________________________________________________________________
Illustration 11:
A line joining two points A(2, 0) and B(3, 1) is rotated about A in the anticlockwise direction through an angle of 15o. Find the equation of the line in the new position. If B goes to C, what will be the coordinates of C, in the new position?
Solution:
Slope of BAB(m) = 1 ⇒ m = tan θ = 1 ⇒ θ = 45o.
= tan (60o) (because angle between AB and AC = 15o).
Also AB = AC = √2 and A is (2, 0).
Hence equation of the line AC is
(x–2)/cos 60o = (y–0)/sin 60o
or (x–2)/1/2 = y/(√3/2) = r = √2
⇒ C is (2 + √2.1/2, 0 + √2.√3/2) i.e. C is (2 + 1/√2, √3/√2).
__________________________________________________________________________
Illustration 12:
Find the distance of the point P(–2, 3) from the line AB which is x – y = 5.
Solution:
The equation of the line is
x – y – 5 = 0 [Making right side zero]
∴ Perpendicular Distance of the point (2, 3)
= (–2)–3–5/√(1)2+(–1)2 = –10/√2
= –5√2
∴ Changing the sign, perpendicular Distance in magnitude = 5√2.
___________________________________________________________________________________
Illustration 13:
Draw the lines 3x + 4y – 12 = 0 and 5x + 12y + 13 = 0. Find the equation of the bisector of the angle containing the origin. Also find the acute angle bisector and obtuse angle bisector.
Solution:
Let us make the expression on the left-hand side of the given equations of the same sign – or + ve. After substituting x = 0 and y = 0.
L.H.S. of (i) is 3.0 + 4.0 – 12 = – 12 = – ve
R.H.S. of (ii) is 5.0 + 12.0 + 13 = 13 = + ve
So, multiply equation (i) by (–1), we get
– 3x – 4y + 12 = 0 …… (1)
Equation of the bisector of the angle containing origin is given by +ve sign i.e. (-3x – 4y + 12)/5 = + (5x + 12y + 13)/13
⇒ 64x + 112y – 91 = 0 …… (3)
Again, the given lines are
– 3x – 4y + 12 = 0 …… (1)
5x + 12y + 13 = 0 …… (2)
To find out whether this is an acute angle bisector or obtuse angle bisector, let us find the sign of a1a2 + b1b2 from equation (1) and equation (2).
a1a2 + b1b2
= (–3)(5) + (–4)(12) = – 15 – 48 = – 63 = – ve
The bisector containing the origin is the acute angle bisector.
Now, for obtuse angle bisector, we take –ve origin.
i.e. (–3x – 4y + 12)/5 = + (5x+12y+13)/13
i.e. 14x – 8y – 221 = 0 …… (4)
Well, to confirm all this, let us find angle between one of the lines and one of the bisectors i.e.
5x + 12y + 13 = 0 …… (2)
64x + 112y – 91 = 0 …… (3)
Slope of line (2) is m2 = –5/12
Slope of line (3) is m3 = –64/112
Let q be the angle between these two lines
⇒ tan θ =  < 1
< 1
∴ 64x + 112y – 91 = 0 is an acute angle bisector.
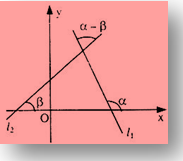
Now, tan (a – b) = (tan α – tan β)/(1 + tan α tan β)
⇒ tan (θ) = (m1 + m2)/(1 + m1m2) (α – β = θ say)
Since lines can be taken in any order and
tan (–θ) = – tan θ. So only the magnitude of θ can be obtained.
Further tan (π–θ) = – tan θ.
Since magnitude also includes the other angle i.e.
Supplementary angle. So θ is given by
tan θacute = 
|
Related Resources
-
You may wish to refer indefinite integral.
-
Click here to refer the most Useful Books of Mathematics.
-
For getting an idea of the type of questions asked, refer the previous year papers.
To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.



 Some important & Interesting Facts
Some important & Interesting Facts where m
where m