Distance between two points

Before we discuss the procedure of finding the distance between points, we shall first throw some light on the position of two points with respect to a given line. These concepts lay the foundation for various other concepts and hence are extremely useful for attempting numerical.

Consider a point (x₁, y₁) and a line ax + by + c = 0. Then, if ax₁ + by₁+ c is of the same sign as ‘c’, then the point (x₁, y₁) lie on the same origin side of ax + by + c = 0 . Conversely, if the sign of c and ax₁ + by₁+ c is opposite, then the point (x₁, y₁) will lie on the non-origin side of ax + by + c = 0.

Let the line be ax + by + c = 0 and P(x₁, y₁), Q(x₂, y₂) be two points. Then, we have two cases:

Case 1:

If P(x₁, y₁) and Q(x₂, y₂) are on the opposite sides of the line ax + by + c = 0, then the point R on the line ax + by + c = 0 divides the line PQ internally in the ratio m₁ : m₂, where m₁/m₂ must be positive.

Co-ordinates of R are {(m₁x₂ + m₂x₁)/(m₁ + m₂₎, (m₁y₂ + m₂y₁)/(m₁ + m₂)}.

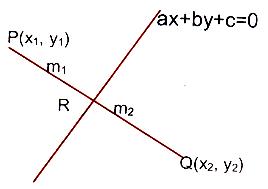Point R lies on the line ax + by + c = 0.

⇒ m₁/m₂ = (ax₁ + by₁ + c)/(ax₂ + by₂ + c) > 0

So that ax₁ + by₁ + c and ax₂ + by₂ + c should have opposite signs.

Case 2:

If ax₁ + by₁ + c and ax₂ + by₂ + c have the same signs then m₁/m₂ = –ve, so that the point R on the line ax + by + c = 0 will divide the line PQ externally in the ratio m₁ : m₂ and the points P(x₁, y₁) and Q(x₂, y₂) are on the same side of the line ax + by + c = 0.

Illustration:

Find the range of θ in the interval (0, π) such that the points (3, 5) and (sin θ, cos θ) lie on the same side of the line x + y – 1 = 0.

Solution:

As discussed above, we know that ax₁ + by₁ + c and ax₂ + by₂ + c both must be of the same signs for the points to be on the same side of the line.

Now, 3 + 5 – 1 = 7 > 0 ⇒ sin θ + cos θ – 1 > 0

⇒ sin(π/4 + θ) > 1/√2

⇒ π/4 < π/4 + θ < 3π/4

⇒ 0 < θ < π/2.

Hence, this is the required range of θ in the interval (0, π) such that the points (3, 5) and (sin θ, cos θ) lie on the same side of the line x + y – 1 = 0.

Illustration:

Find α, if (α, α²) lies inside the triangle having sides along the lines 2x + 3y = 1, x + 2y – 3 = 0, 6y = 5x – 1.

Solution:

Let A, B, C be vertices of the triangle.

A ≡ (–7, 5), B ≡ (5/4, 7/8) and C ≡ (1/3, 1/9).

Sign of A w.r.t. BC is –ve.

If P lies inside the ?ABC, then sign of P will be the same as sign of A w.r.t. the line BC

⇒ 5α – 6α² – 1 < 0.                     …… (1)

Similarly 2α + 3α² – 1 > 0.          …… (2)

And, α + 2α² – 3 < 0.                  …… (3)

Solving, (1), (2) and (3) for α and then taking intersection,

We get α ∈ (1/2, 1) ∪ (–3/2, –1).

_____________________________________ 

Illustration:

The equations of the perpendicular bisectors of the sides AB and AC of a triangle ABC are respectively x – y + 5 = 0 and x + 2y = 0. If the co-ordinates of A are (1, –2), find the equation of BC.

Solution:

From the figure, since OE and OF are the perpendicular bisectors of the sides AB and AC, so we have the coordinates of points E and F as

E ≡ (x₁ + 1/2, y₁ - 2/2),

F ≡ (x₂ + 1/2, y₂ - 2/2).

Since E and F lie on OE and OF respectively,

x₁ – y₁ + 13 = 0                                  … (1)

and x₂ + 2y₂ – 3 = 0                           … (2)

Also, slope of AB = –1 and slope of AC is 2, so that

x₁ + y₁ + 1 = 0.                                   … (3)

And 2x₂ – y₂ – 4 = 0                           … (4)

Solving these equations, we get the co-ordinates of B and C as

B ≡ (–7, 6) and C ≡ (11/5, 2/5)

⇒ Equation of BC is 14x + 23y – 40 = 0.

Illustration:

Two fixed points A and B are taken on the co-ordinate axes such that OA = a and OB = b. Two variable points A’ and B’ are taken on the same axes such that OA’ + OB’ = OA + OB. Find the locus of the point of intersection of AB’ and A’B.

Solution:

Let A ≡ (a, 0), B (0, b), A’ ≡ (a’, 0), B’ ≡ (0, b’).

Equation of A’B is x/a' + y/b' = 1.                                          …. (1)

and equation of AB’ is x/a + y/b'  = 1.                                   …. (2)

Subtracting (1) from (2), we get, x (1/a – 1/a') + y(1/b' – 1/b) = 0.

⇒ x(a'–a)/aa' + y(b–b')/bb' = 0.                   [Using a’ – a = b – b’]

⇒ x/a(b–b'+a) + y/bb' = 0 

⇒ b’ = a(a+b)y/ay–bx.                   ….. (3)

From (2), b’x + ay = ab’   ….. (4) we get x + y = a + b which is the required locus.

The distance between two points P(x₁, y₁) and Q(x₂, y₂) is (see the figure given below).

Length PQ = √(x₂ – x₁)² + (y₂ – y₁)²

Proof:

Let P(x₁, y₁) and Q(x₂, y₂) be the two points and let the distance between them be ‘d’. Draw PA, QR parallel to y-axis and PR parallel to x-axis. 

Angle QRP = 90^o  

⇒ d² = PR² + RQ² 

⇒ d² = (x₂ – x₁)² + (y₂ – y₁)²

⇒ d = √(x₂ – x₁)² + (y₂ – y₁)². 

You may also view the video on distance formula

Similarly, in three dimensions, we shall have a third coordinate and the formula in that case changes a bit:

Distance between P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) is given by the formula d = √(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)².

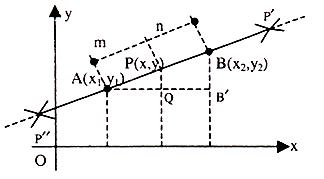
Let us say we want to know the co-ordinates of point which divides a line segment between two points A(x₁, y₁) and B(x₂, y₂) in the ratio m : n. Then two types of division are possible:

The coordinates of such a point are given by:

Internal Division: {(nx₁ + mx₂)/(m + n), (ny₁ + my₂)/(m + n)}

External Division:  {(mx₂ - nx₁)/(m - n), (my₂ - ny₁)/(m - n)}

Note: 

This is called section formula. 

Let P divide the line segment AB in the ratio m : n. If P is inside AB then it is called internal division; if it is outside AB then it is called external division. 

However in each case AP/BP [or AP'/BP' or AP"/BP"] = m/n.  

Proof: 

Consider ? ABB’  

Since BB’||PQ and AP:PB = m:n (see figure given below)

AQ/AB' = PQ/BB' = m/(m+n) (= AP/AB) 

⇒ x – x₁/x₂ – x₁ = m/(m+n) 

⇒ x = (nx₁ + mx₂)/(m + n) and y = (ny₁ + my₂)/(m + n) 

If P is outside AB (less assume it is at P’) 

We have (x – x₁)/(x₂ – x₁) = m/(m + n) 

⇒ x = (nx₁ + mx₂)/(m + n) and y = (ny₁ + my₂)/(m + n) 

Similarly if P is at P” then 

x = (–mx₂ + nx₁)/(n-m), y = (– my₂ + ny₁)/(n-m)

Note:  

m:n can be written as m/n or λ:1. So any point on line joining A and B will be P{(λx² + x₁)/(λ + 1), (λy² + y₁)/(λ +1)}. It is useful to assume λ:1 because it involves only one variable. 

Illustration: 

Prove that altitudes of a triangle are concurrent and prove that the co-ordinates of the point of con-currency are {(x₁ tan A + x₂ tan B + x₃ tan C)/(tan A + tan B + tan C), (y₁ tan A + y₂ tan B + y₃ tan C)/(tan A + tan B + tan C)}. 

Solution: 

In triangle A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃), draw AD perpendicular to BC. Our effort now should be to find the co-ordinates of the point D.

To do that, we need to find BC/CD. (figure is given above) 

tan B = AD/BD and tan C = AD/CD 

⇒ BD/DC = tan C/tan B 

Now we apply section formulae: 

x_D = (x₂ tan B + x₃ tan C)/(tan B + tan C)                           …… (i)

y_D = (y₂ tan B + y₃ tan C)/(tan B + tan C)                               …… (ii)

We know that orthocenter will lie on AD. We need to find this point and its co-ordinates. 

We should select a point H₁ on AD and take the ratio AH₁/H₁D in such a manner so that x_H1 and y_H1 calculated form (i) should be symmetric in x₁, x₂, x₃, tan A, tan B and tan C.

Let AH₁/H₁D = (tan B + tan C)/tan A 

⇒ xH₁ = (x₁ tan A + x₂ tan B + x₃ tan C)/(tan A + tan B + tan C)

and ⇒ yH₁ = (y₁ tan A + y₂ tan B + y₃ tan C)/(tan A + tan B + tan C) 

Since the result is symmetric, this point H1 will lie on other altitude as well i.e. the altitudes are concurrent

⇒ xH = xH₁ and yH = yH₁.

___________________________________________________________________________

Prove analytically that in a right angled triangle the midpoint of the hypotenuse is equidistant from the three angular points. 

Solution: 

While proving a problem analytically take most convenient co-ordinates of known points. 

In the present case triangle is assumed as AOB with coordinates as shown in figure given below, C is midpoint of AB.

So co-ordinates of C will be (a/2, b/2) 

Now AB = √a² + b²

CA = CB = AB/2 (C is mid point of AB) 

= √a² + b² 

And, we know that the distance between two points C and O is given by 

CO = √(a/2 – 0)² + (b/2 – 0)² = √a² + b²/2 

Hence CA = CB = CO 

Coordinates of the point P dividing the join of two points A(x₁, y₁) and B(x₂, y₂) internally in the given ratio λ₁ : λ₂ i.e., AP/BP = λ₁/λ₂ are P {(λ₂x₁ + λ₁x₂)/(λ₂ + λ₁), (λ₂y₁ + λ₁y₂)/(λ₂ + λ₁)}. 

Coordinates of the point P dividing the join of two points A(x₁, y₁) and B(x₂, y₂) externally in the ratio λ₁ : λ₂ i.e., AO/BP = λ₁/λ₂ are P(λ₂x₁+λ₁x₂)/(λ₂–λ₁), (λ₂y₁+λ₁y₂)/(λ₂–λ₁).
 

Related Resources

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.