Distance between two Parallel Lines
In this section, we shall discuss how to find the distance between two parallel lines. But before doing that, let us first throw some light on the concept of parallel lines.
When two straight lines are parallel, their slopes are equal. Hence, any line parallel to the line sx + ty + c = 0 is of the form sx + ty + k = 0, where k is a parameter.
How do we calculate the distance between Parallel Lines?
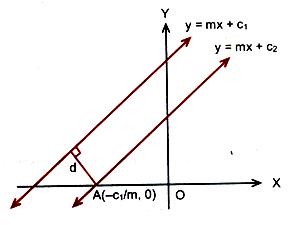
We know that slopes of two parallel lines are equal. Therefore, two parallel lines can be taken in the form
y = mx + c1 … (1)
and y = mx + c2 … (2)
Line (1) will intersect x-axis at the point A (–c1/m, 0) as shown in figure.
Distance between two lines is equal to the length of the perpendicular from point A to line (2). Therefore, distance between the lines (1) and (2) is
|(–m)(–c1/m) + (–c2)|/√(1 + m2) or d = |c1–c2|/√(1+m2).
Thus the distance d between two parallel liens y = mx + c1 and y = mx + c2 is given by d = |C1–C2|/√A2 + B2.
Result:
The area of a parallelogram is also based on the concept of distance between parallel lines.
The area of a paralellogram = p1p2/sin θ, where p1 and p2 are distances between two pairs of opposite sides and θ is the angle between any two adjacent sides.
Hence, the area of the parallelogram bounded by the lines y = m1x + c1, y = m1x + c2 and y = m2x + d1, y = m2x + d2 is given by |(c1-c2)(d1-d2)/ (m1-m2)|.
Illustration:
Find the distance of the point (3, –5) from the line 3x – 4y – 26 = 0.
Solution:
Given line is 3x – 4y – 26 = 0. …… (1)
Comparing (1) with general equation of line Ax + By + C = 0, we get
A = 3, B = –4 and C = –26.
Given point is (x1, y1) = (3, –5). The distance of the given point from given line is d = |Ax1 + By1 + C|/√A2+B2 = 3/5.
Illustration:
Find the distance between the parallel lines 3x – 4y + 7 = 0 and 3x – 4y + 5 = 0.
Solution:
Here A = 3, B = –4, C1 = 7 and C2 = 5.
Therefore, the required distance is d = |7–5|/√32+(–4)2 = 2/5.
Illustration:
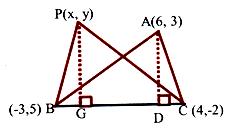
The coordinates of the vertices A, B, C of a triangle are (6, 3), (–3, 5) and (4,–2) respectively and P is any point (x, y). Show that the ratio of the areas of the triangles PBC and ABC is |x + y – 2| : 7.
Solution:
Equation of the line BC is x + y – 2 = 0. Let PG and AD be perpendiculars from P and A on BC.
Ratio of areas of triangles PBC and ABC is
1/2.BC.PG/1/2.BC.AD = PG/AD. But PG is the length of the perpendicular form P(x, y) on x + y – 2 = 0 and AD is the length of the perpendicular from A(6, 3) on x + y – 2 = 0.
⇒ Ratio of the areas of triangle PBC and triangle ABC.
⇒ |x+y–2/√2|/|6+3–2/√2| = |x+y–2/7|.
Illustration:
Find the distance from the line 3x – 4y + 35 = 0 of the point (0, 0).
Solution:
Writing the given equation in the normal form, we get
–3/5 x + 4/5 y – 7 = 0
Substituting x = 0, y = 0 in it, d = –3/5 (0) + 4/5 (0) – 7 = –7
Changing sign the required distance = 7.
Another form
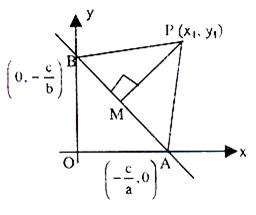
To find the perpendicular distance of the point (x1, y1) from the line ax + by + c = 0.
Let us convert the given equation in the normal form.
a/√a2+b2 x + b/√a2+b2 y + c/√a2+b2 = 0
∴ The perpendicular Distance of (x1, y1) is
d = a/√a2 + b2x1 + b/√a2 + b2 y1 + c/√a2 + b2
d = ax1+by1+c/√a2 + b2
This formula can also be obtained independently as under:
Let PM be the perpendicular form P on AB. Then coordinates of A and B are (–c/a, 0) and (0, –c/b) respectively,
AB = √c2/a2+c2/b2
= c/ab √(a2+b2)
Area of traingle PAB
= 1/2 [x1 (–c/b – 0)+0(0 – y1) – c/a (y1 + c/b)]
= –c/2ab (ax1 + by1 + c) …… (1)
Also, area of triangle PAB = ½ PM.AB
= 1/2 PM.c/ab √(a2+b2) …… (2)
From (1) and (2), we have
1/2 PM.c/ab √(a2+b2) (ax1 + by1 + c)
⇒ PM = ax1+by1+c/√a2+b2
Neglecting the negative sign, as the length of a segment is always positive, we have PM = |ax1+by1+c/√a2+b2|.
Watch this Video for more reference
Illustration:
A straight line through the origin O meets the parallel lines 4x + 2y = 9 and 2x + y + 6 = 0 at points P and Q respectively. Then, the point O divides the segment PQ in the ratio (IIT JEE 2000)
(a) 1:2 (b) 3:4
(c) 2:1 (d) 4:3
Solution:
The given parallel lines are 4x + 2y = 9 and 2x + y + 6 = 0.
The distance of the origin from 4x + 2y – 9 = 0 is |-9|/√42 + 22 = 9/√20.
Similarly, the distance of origin from 2x+ y + 6 = 0 is
|6|/√22 + 12 = 6/√5.
Hence, the required ratio is (9/√20) / (6/√5) = ¾.
Related Resources
-
Click here to refer the most Useful Books of Mathematics.
-
For getting an idea of the type of questions asked, refer the previous year papers.
To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.