Different Forms of Line
Table of Content |
Straight line is an extremely important and a vast topic of the mathematics syllabus of IIT JEE. Students are advised to go into the intricacies of topics in order to master them. In this section, we shall discuss the equation of straight line in various forms and illustrate the concepts along with certain examples as well. Aspirants must try to grasp these concepts in order to excel in competitions like the IIT JEE.
What do you mean by the equation of a Straight Line?
A certain kind of relation between the variables x and y which is met by the coordinates of every point lying on a line is termed as the equation of a straight line.
Remark:
-
Any linear equation in two variables x and y always represents a straight line.
-
Equation of a line which is parallel to x-axis or perpendicular to y-axis at a distance ‘c’ from it is given as y = c.
-
Equation of a line which is parallel to y-axis or perpendicular to x-axis at a distance ‘c’ from it is given as x = c.
?We now discuss the various forms of lines one by one:
The most general equation of a straight line is ax + by + c = 0, where a, b and c are any real numbers such that both a and b can’t be zero simultaneously.
If we have a straight line whose slope is ‘m’ and which makes an intercept ‘c’ on the y-axis then its equation is given by y = mx + c.
As shown in the figure above, the y-intercept here is c.
The equation of a straight line having slope as ‘m’ and which passes through the point (x1, y1) is given by (y-y1) = m(x-x1).
Consider line PQ with coordinates P(x, y) and Q(x1, y1). Then Co-ordinates of any points P(x, y) are
x = x1 + r cos θ (see figure given below)
y = y1 + r sin θ
Equation of the line is obtained as follows:-
⇒ x–x1/cos θ = y–y1/sin θ = r
This is parametric form of the equation of a straight line.
Note:
1. Note that ‘r’ is positive if the point (x, y) lies on the right of (x1, y1) and negative if the point (x, y) lies on the left of (x1, y1).
If we have two given points say (x1, y1) and (x2, y2), then the line passing through them is given by the formula
(y-y1) = m(x-x1) or (y-y1) = (y2-y1)/(x2-x1). (x-x1).
If intercepts of a line on x and y-axis are known then equation of the line can also be found in two-intercept form. Intercepts are OA and OB on x and y-axis respectively, where A(a, 0) and B(0, b) are two points through which line is passing. Treating it as a special case of two-point form, one can write a unique equation of the line as
y–0/x–a = 0–b/a–0, where P(x, y) is any point on the line (figure given below)
If we are given the intercepts of a line on the x and y axis respectively as ‘a’ and ‘b’ then the equation of the straight line is given by x/a + y/b = 1.
⇒ y/b = –x/a + 1.
⇒ x/a + y/b = 1.
This is intercept from of the equation of a straight line.
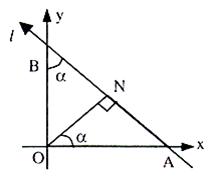
x cos α + y sin α = a is the equation of the straight line in perpendicular form, where ‘p’ is the length of the perpendicular from the origin O on the line and this perpendicular makes an angle α with the positive direction of x-axis.
Consider line l as shown in figure given above
ON ⊥ l and |ON| = p
We have in triangle ONA
OA = p/cos α
A and B are intercept points of line l. So intercepts on x and y-axes are p/cos α and p/sin α respectively. So equation of line l will be (both intercept form)
⇒ x cos α + y sin α = p
This is the equation of a straight line in normal form, where p is perpendicular distance of the line from origin.
Note:
P is always measured away from the origin and is always positive in value, αa is a positive angle less than 360o measured from the positive direction OX of the x-axis to the normal from the origin to the line.
Reduction of General form of Equations into Standard Forms
The general form of equation is ax + by + c = 0, then we can derive the other forms as:
Slope-intercept form: This form is given by y = -a/b x -c/b, where slope = – a/b and intercept is -c/b
Intercept form: This form is given as x/(-c/a) + y/(-c/b) = 1, here x-intercept is (-c/a) and y-intercept is (-c/b).
Normal Form: In order to change the general form of equation to the normal form, first take ‘c’ to the right side and try to make it positive. Then the whole equation should be divided by √a2 + b2 like
-ax/√(a2 + b2) – by/√(a2 + b2) = c/√(a2 + b2), where
cos α = -a/√(a2 + b2), sin α = -b/√(a2 + b2) and p = c/√(a2 + b2).
Now, we discuss some of illustrations based on this concept:
Illustration:
The ends of a rod of length l move on two mutually perpendicular lines. Find the locus of the point on the rod, which divides it in the ratio 2 : 1.
Solution:
Suppose the two perpendicular lines are x = 0 and y = 0 and let the end of the rod lie at the point (0, a) and (b, 0).
The point P has coordinates given by
h = b+2.0/2+1, k = 2.a+1.0/2+1
⇒ a = 3k/2, b = 3h.
Also l2 = a2 + b2.
⇒ l2 = (3k/2)2 + (3h)2.
Thus the required locus is
x2 + y2/4 = l2/9, which represents an ellipse.
Similarly, take the ratio AP : BP as 2 : 1 and proceed. We get the result as y2 + x2/4 = l2/9.
Illustration:
Find the locus of the point of intersection of the lines x cos α + y sin α = a and x sin α – y cos α = b. where α is a variable.
Solution:
Let P(h, k) be the point of intersection of the given lines.
Then h cos α + k sin α = a. … (1)
h sin α – k cos α = b. … (2)
Here a is a variable. So we have to eliminate a.
Squaring and adding (1) and (2),
We get, (hcos α + ksin α)2 + (hsin α – kcos α)2 = a2 + b2
⇒ h2 + k2 = a2 + b2.
Hence locus of (h, k) is x2 + y2 = a2 + b2.
Related Resources
-
Click here to refer the most Useful Books of Mathematics.
-
For getting an idea of the type of questions asked, refer the previous year papers.
To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.