Combined Equations of Angle Bisectors of Lines
Combined equations of the angle bisectors of the lines represented by ax2 + 2hxy +by2 = 0
y – m1x = 0 and y – m2x = 0
Let P(α, ß) be any point on one of bisectors.
⇒ (ß–m1α)/√1+m12 = + ß–m2α/√1+m22
⇒ (1 + m22) (ß – m1α)2 – (1 + m12) (ß – m2α)2 = 0
⇒ Locus of P(α, ß) is
x2 – y2 = 2hxy 1–m1m2/m1+m1
⇒ x2–y2/a–b = xy/h; is required equation of angle bisectors …… (1)
Note:
1. If a = b, then bisectors are x2 – y2 = 0 i.e. x – y = 0, x + y = 0
2. If h = 0, the bisectors are xy = 0 i.e. x = 0, y = 0
3. If in (i), coefficien
t of x2 + coefficient of 2 = 0, then the two bisectors are always perpendicular to each other
t of x2 + coefficient of 2 = 0, then the two bisectors are always perpendicular to each other
Illustration:
Prove that the angle between one of the lines given by
ax2 + 2hxy + by2 = 0 and one of the lines given by ax2 + 2hxy+ by2 + K(x2 + y2) = 0 is equal to the angle between the other two lines of the system.
ax2 + 2hxy + by2 = 0 and one of the lines given by ax2 + 2hxy+ by2 + K(x2 + y2) = 0 is equal to the angle between the other two lines of the system.
Solution:
Let L1 and L2 be one pair and L3 and L4 be the other pair of lines.
If the angle between L1 and L3 is equal to the angle between L2 and L4 then pair of bisectors of L1 and L2 would be same as that of L3 and L4. Pair of bisectors of L3 and L4 is
x2–y2/(a+k)–(b+k) = xy/h
⇒ x2–y2/a–b = xy/h
Which is the same as the bisector pair of L1 and L2.
6. Angle bisectors of ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 (i) are given by (x–x0)2–(y–y0)2/a–b = (x–x0)(y–y0)/h where (x0, y0) is the point of intersection of (i)
Enquiry: If we shift the origin of the coordinate system how can the coordinates of a point be known in the new system? What will happen if we rotate the axis?
(i) Linear Transformation:
CP = x, DP = y; AP = x, BP = y
If origin is shifted to (h, k) then the coordinates of a point
P(x, y) in the new system are
P(x, y) in the new system are
X = x – h
Y = y – k
You can check it by putting (h = 0, k = 0) that it gets reduced to the same original coordinate system.
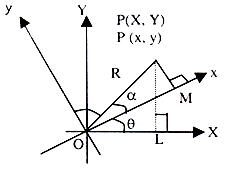
(ii) Rotation of Axes:
If axes are rotated anticlockwise by angle q then the coordinates of a point P(x, y) changes to say P(x, y):
OL = x, PL = y
OM = X, PM = Y
OP = R (say)
cos (α + θ) = x/R …… (i)
sin (α + θ) = Y/R …… (ii)
cos α = x/R …… (ii)
sin α = Y/R …… (iv)
Eliminating α from (i), (ii), (iii) and (iv) we get
X = x cos θ + y sin θ
Y = –x sin θ + y cos θ
It can be checked that if θ = 0; then coordinates remain unchanged.
Illustration:
Find the equation of the line 2x + y = 7 when co-ordinates system is shifted to the point (3, 1)
Solution:
x = 3 + X and y = 1 + Y
Equation of line becomes
2(3 + X) + (1 + Y) = 7
or 2X + Y = 0
Note:
Slope of the line remains the same.
The general equation of second degree ax2 + 2hxy + by2 + 2gx + 2fy + c=0 represents a pair of straight lines if  = 0.
= 0.
 = 0.
= 0.⇒ abc + 2fgh – af2 – bg2 – ch2 = 0 and h2 > ab.
The homogeneous second degree equation ax2 + 2hxy + by2 = 0 represents a pair of straight lines through the origin.
If lines through the origin whose joint equation is ax2 + 2hxy + by2 = 0, are y = m1x and y = m2x, then y2 – (m1 + m2)xy + m1m2x2 = 0 and y2 + 2h/b xy + a/b x2 = 0 are identical. If θ is the angle between the two lines, then tanθ = + √(m1+m2)2–4m1m2/1+m1m2 = + 2√h2–ab/a+b.
The lines are perpendicular if a + b = 0 and coincident if h2 = ab.
To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.