Area of a triangle
Table of Content |
Let (x1, y1), (x2, y2) and (x3, y3) be the coordinates of the vertices A, B and C of triangle ABC, then the area of triangle ABC is given by
|1/2[x1(y2 – y3) + x2(y3 + y1) + x3(y1 – y2)]|
which can also be represented as
= 
.
If the vertices are taken in counter clockwise direction, then the area is positive. But, if the vertices are placed in the clockwise direction, then the area would be negative. Hence, in order to avoid the negative area, the value is placed in modulus.
Area of a Polygon of n Sides
Suppose there is a polygon with vertices A1(x1, y1), A(x2, y2), …, An(xn, yn) in anticlockwise order. Then the area of the polygon is given by the formula
= 
which can be written as
= 1/2|(x1y2 – y1x2) + (x2y3 – y2x3) + …. + (xn-1yn – yn-1xn)) + (xny1 – ynx1)|.
Collinearity of three given points
Another concept that is related to the concept of area is of collinearity of three given points. If we have three points which are collinear then the area of the triangle formed by these points is zero. In fact, any three points (say) A, B and C are said to be collinear if any one of the following conditions is satisfied:
-
Area of triangle ABC is zero.
-
The slopes of all three lines are same i.e. slope of line AB = slope of BC = slope of AC.
-
AC = AB + BC
-
If the points are collinear, then the equation of the line passing through the intersection of 2 given points must be satisfied by the third point. If not, the points are not collinear.
-
It follows that the three points (x1, y1), (x2, y2) and (x3, y3) will be collinear if
?
= 0.
-
If three points P1, P2 and P3 are collinear then the determinant at must vanish i.e. the area of triangle formed must be zero.
Illustration:
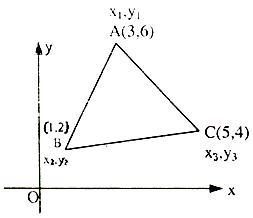
Calculate area of a triangle shown in figures given below.
Solution:
Using the just derived formula
Area of a triangle is given by
1/2 [3(2 – 4) + (1) (4 – 6) + 5 (6 – 2)]
= 1/2 [– 6 – 2 + 20]
= 6
Similarly, area of the triangle shown in the figure given above.
Area of a traingle ABC is
= 1/2 [3(4 – 2) + (5) (2 – 6) + (1) (6 – 4)]
= 1/2 [6 – 20 + 2]
= – 6.
Note:
Thus we observe that the area of a triangle is positive if vertices are taken in the anticlockwise direction and negative when the vertices are taken the clockwise direction.
Area of a triangle can also be expressed as = 1/2 
= 1/2 [x1 y2 – y1 x2 + x2 y3 – y2 x3 + x3 y1 – y3 x1]
This form is important. It can be used to find area of a quadrilateral, pentagon, hexagon and polygons.
Watch this Video for more reference
Illustration:
Prove that the area of the triangle with vertices at (p – 4, p + 5), (p + 3, p – 2) and (p, p) remains constant as p varies.
Solution:
The area of the triangle is
which remains constant for all values of p.
Illustration:
All points lying inside the triangle formed by the points (1, 3), (5, 0) and (-1, 2) satisfy (IIT JEE 1986)
1. 3x + 2y ≥ 0 2. 2x + y – 13 ≥ 0
?3. 2x – 3y – 12 ≤ 0 4. -2x + y ≥ 0
Solution:
We shall proceed in this question by considering each option one by one.
The first one is 3x + 2y ≥ 0 ...(1)
Now, we see that the points (1, 3), (5, 0) and (-1, 2) satisfy the above equation and hence this option is correct.
Similarly, 2x + y – 13 ≥ 0 is not correct since the point (1, 3) does not satisfy it.
Again, option 2x – 3y – 12 ≤ 0 is also correct since it is satisfied for all points.
The fourth option i.e. -2x + y ≥ 0 is not correct since it is not satisfied by the point (5, 0).
Hence, this option is also incorrect.
This means that options 1 and 3 are correct.
Related Resources
-
Click here to refer the most Useful Books of Mathematics.
-
For getting an idea of the type of questions asked, refer the previous year papers.
To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.