Angle Bisectors

Table of Content

What is an Angle Bisector?
How can we differentiate between the Acute Angle Bisector and the Obtuse Angle Bisector?
Another way of identifying the Acute Angle Bisectors and Obtuse Angle Bisectors
Combined Equations of Angle Bisectors of Lines
Related Resources

The concept of angle bisector is an important head under straight lines. Questions are often framed on this topic in various competitions like the IIT JEE. Hence, it is crucial to understand the acute angle bisector and the obtuse angle bisector in order to be successful in such exams. In this section, we shall discuss the angle bisector definition, followed by the concept of bisector of an angle.

What is an Angle Bisector?

Angle bisector of two lines i.e. the line which bisects the angle between the two lines is the locus of a point which is equidistant from the two lines. In other words, an angle bisector has equal perpendicular distance from the two lines.

Let us now try to find the equation of angle bisector. Consider the figure given below:

Suppose we have two lines

L₁ : A₁x + B₁y + C₁ = 0

L₂ : A₂x + B₂y + C₂ = 0

If point R(p, q) lies on the bisector, then length of perpendicular from the point R to both the lines should be equal.

i.e.

Generalizing for any point (x, y), the equation of the angle bisector is obtained as:

(A1x + B1y + C1)/√(A12 + B12) = + (A2 x+ B2y + C2)/√(A22 + B22)

Note:

This equation gives two bisectors: one-acute angle bisector and the other obtuse bisector.

How can we differentiate between the Acute Angle Bisector and the Obtuse Angle Bisector?

It is very simple to determine whether the bisector is an acute angle bisector or an obtuse angle bisector. Compute the angle between the the initial line and one of the bisectors. Suppose that angle is θ. Then find tangent of this angle θ.

In case |tan θ| < 1, then we have 2θ < 90° and so this represents the acute angle bisector.
On the other hand, if |tan θ| > 1, then this represents the obtuse angle bisector.

Remark:

To determine a bisector which lies in the same relative position with respect to the lines as a given point S(x₃, y₃) does, make the signs of the expressions A₁x₃ + B₁y₃+ C1 and A₂x₃ + B₂y₃ + C₂ identical. (say positive) then (A₁x + B₁y + C₁)/√(A₁² + B₁²) = ± (A₂x + B₂y + C₂)/√(A₂²+ B₂²) gives the bisector towards this point. If the signs are different multiply one of the equations with ‘–1’ throughout, so that positive sign is obtained. Then above equation with changed equations of lines will given the required bisector.

If (x₃, y₃) ≡ (0, 0) and A₂A₁ + B₂B₁ > 0 then the bisector towards the origin is the obtuse angle bisector.

Result:

Suppose we have two lines represented by the equations

a₁x + b₁y+ c₁ = 0 and a₂x + b₂y + c₂ = 0.

Then, the equations of the bisectors are

(a₁x + b₁y + c₁)/√(a₁² + b₁²) = + (a₂x + b₂y + c₂)/√(a₂²+ b₂²).

AP is the bisector of an acute angle if,

tan (∠PAN) = tan (θ/2) is such that |tan θ/2| < 1.

AP is an obtuse angle bisector if,

tan (∠PAN) = tan (θ/2) is such that |tan θ/2| > 1.

Note:

1. When both c₁ and c₂ are of the same sign, evaluate a₁a₂ + b₁b₂. If negative, then acute angle bisector is (a₁x + b₁y + c₁)/√(a₁² + b₁²) = + (a₂x + b₂y + c₂)/√(a₂² + b₂²).

2. When both c₁ and c₂ are of the same sign, the equation of the bisector of the angle which contains the origin is (a₁x + b₁y + c₁)/√(a₁²+ b₁²) = + (a₂x + b₂y + c₂)/√(a₂² + b₂²).

3. Bisectors of the angle containing the point (α, ß) is (a₁x + b₁y + c₁)/√(a₁² + b₁²) = + (a₂x + b₂y + c₂)/√(a₂² + b₂²) if a₁α + b₁ß + c₁ and a₂α + b₂ß + c₂ have the same sign.

4. Bisectors of the angle containing the point (α, ß) is (a₁x + b₁y + c₁)/√(a₁² + b₁²) = + (a₂x + b₂y + c₂)/√(a₂² + b₂²) if a₁α + b₁ß + c₁ and a₂α + b₂ß + c₂ have the opposite sign.

Another way of identifying the Acute Angle Bisectors and Obtuse Angle Bisectors

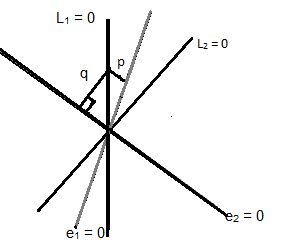
Suppose we have two lines L₁= 0 and L₂ = 0 and e₁ = 0 and e₂ = 0 are the bisectors between these two lines. We take a point R on one of these lines and draw perpendiculars on e₁and e₂.

If |p| < |q|, then e₁ is the acute angle bisector.

If |p| > |q|, then e₁ is the obtuse angle bisector.

If |p| = |q|, then the lines L₁ and L₂ are perpendicular.

Note:

Equation of straight lines passing through P(x₁, y₁) and which are equally inclined with the lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 are the ones which are aparllel to teh bisectors between these two lines and they pass through the point P.

Illustration:

For the straight lines 4x + 3y – 6 = 0 and 5x + 12y + 9 = 0 , find the equation of the

bisector of the obtuse angle between them
bisector of the acute angle between them,
bisector of the angle which contains (1, 2)

Solution:

Equations of bisectors of the angles between the given lines are

(4x + 3y – 6)/√(42 + 32) = + (5x + 12y + 9)/√(52 +122)

⇒9x – 7y – 41 = 0 and 7x + 9y – 3 = 0.

If θ is the angle between the line 4x + 3y – 6 = 0 and the bisector 9x – 7y – 41 = 0, then tan θ ≥ 1.

Hence, the bisector of the obtuse angle is 9x – 7y – 41 = 0 and the bisector of the acute angle is 7x + 9y – 3 = 0.

For the point (1, 2), we have

4x + 3y – 6 = 4 × 1 + 3 × 2 – 6 > 0\

5x + 12y + 9 = 12 × 12 + 9 > 0.

Hence equation of the bisector of the angle containing the point (1, 2) is 4x + 3y – 6/5 = 5x + 12y + 9/13 ⇒ 9x – 7y – 41 = 0.

Combined Equations of Angle Bisectors of Lines

We try to compute the combined equations of angle bisectors of lines represented by ax² + 2hxy + by² = 0.

Let ax2 + 2hxy + by2 = 9 represent lines y – m1x = 0 and y – m2x = 0

Let P(α, ß) be any point on one of bisectors.

⇒ (ß–m1α)/√(1 + m12) = + (ß–m₂α) /√(1 + m22)

⇒ (1 + m22) (ß – m1α)2 – (1 + m12) (ß – m2α)2 = 0

⇒ Locus of P(α, ß) is x2 – y2 = 2hxy

⇒ (x2–y2) /(a–b) = xy/h; is required equation of angle bisectors …… (1)

Note:

If a = b, then bisectors are x² – y² = 0 i.e. x – y = 0, x + y = 0
If h = 0, the bisectors are xy = 0 i.e. x = 0, y = 0
If in (i), coefficient of x² + coefficient of y² = 0, then the two bisectors are always perpendicular to each other

Illustration:

Prove that the angle between one of the lines given by
ax² + 2hxy + by² = 0 and one of the lines given by ax² + 2hxy+ by² + K(x² + y²) = 0 is equal to the angle between the other two lines of the system.

Solution:

Let L₁ and L₂ be one pair and L₃ and L₄ be the other pair of lines.

If the angle between L1 and L3 is equal to the angle between L2 and L4 then pair of bisectors of L1 and L2 would be same as that of L3 and L4.

Pair of bisectors of L3 and L4 is

(x2–y2) /(a+k) – (b+k) = xy/h

⇒ (x2 – y2)/(a–b) = xy/h

Which is the same as the bisector pair of L1 and L2.

Angle bisectors of ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 (i) are given by (x–x0)2–(y–y0)2/a–b = (x–x0)(y–y0)/h where (x0, y0) is the point of intersection of (i)

Illustration:

Let P = (-1, 0), Q = (0, 0) and R = (3, 3√3) be three points. Then, the equations of the bisector of the angle PQR is (IIT JEE 2002)

(a) √3/2 x + y = 0 (b) x + √3y = 0

Solution:

The line segment QR makes an angle of 60° with the positive direction of x-axis.

Hence, the bisector of the angle PQR will make an angle of 60° with the negative direction of x-axis and hence, the inclination would be of 120.

Its equation is given by y-0 = tan 120°(x-0)

This gives y = - √3x

Hence, y + √3x = 0.

Illustration:

Find the equation of the bisector of the acute angle between the lines 3x – 4y + 7 = 0 and 12x + 5y – 2 = 0.

Solution:

The given equations can be rewritten as 3x – 4y + 7 = 0 and -12x - 5y + 2 = 0.

Here, a₁a₂ + b₁b₂ = 3(-12) – 4(-5) < 0

And hence, the positive sign gives us the acute angle bisector which is 3x – 4y + 7/5 = -12x – 5y + 2/13.

This yields 99x – 27y + 81 = 0.

Hence, the required equation is 11x – 3y + 9 = 0.

Related Resources

Click here to refer the most Useful Books of Mathematics.
For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.