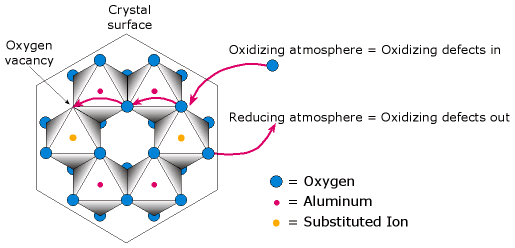
Structure of Ionic Compounds

Table of Content

Structure Determination by X – Rays
Ionic Compounds of the type AB
Ionic compound of AB2 type
- Fluorite Structures
Ionic compound of A2B type
Related Resources

Structure Determination by X – Rays

The German physicist M Von Laue (1879 – 1960) in 1913 suggested the possibility of diffraction of X – Rays by crystals.
The reason for this suggestion was that the wavelength of X – Rays was of about the same order as the inter atomic distances in a crystal.
Then if these X – Rays was allowed to strike the crystal the rays will penetrate into the crystal and will be scattered by the electrons of the atoms or the ions of the crystal.

?The rays reflected from different layers of the atoms, due to wave nature will then undergo interference ( constructive and destructive) to produce a diffraction pattern just as it happens in case of light passing through a grating containing a large number of closely spaced lines. In other words, crystals should act as a three dimensional grating for X – Rays. Bragg applied this fact in determining structure and dimensions of crystal.
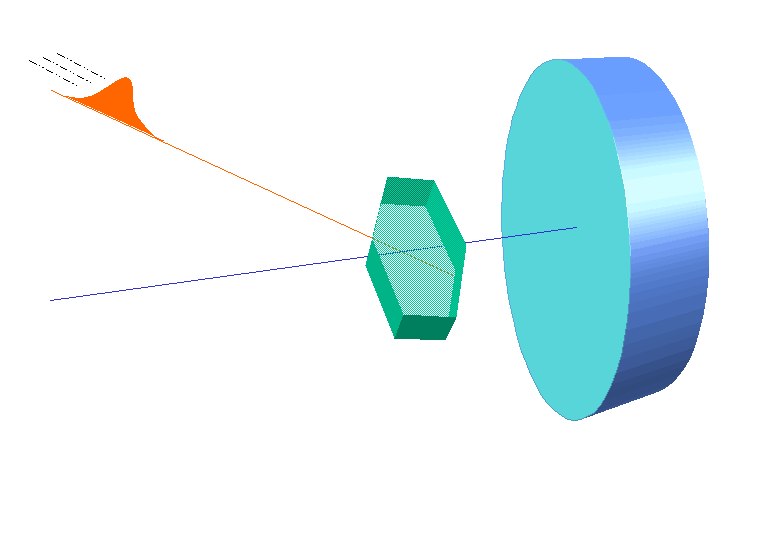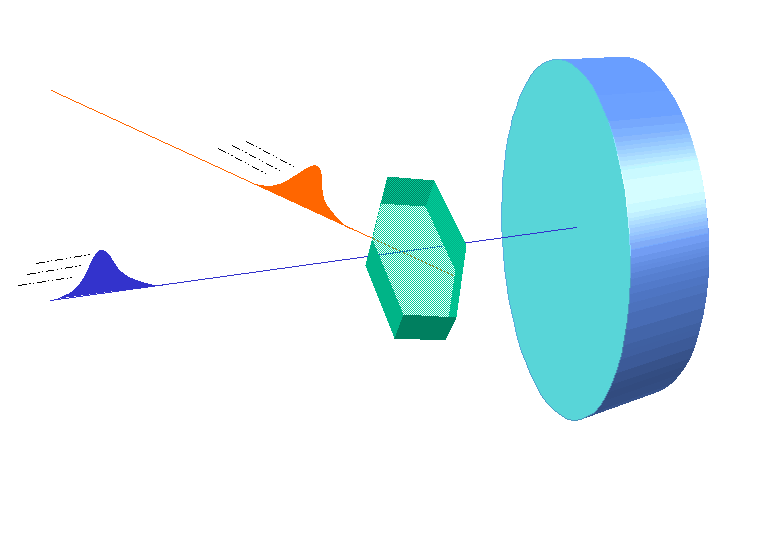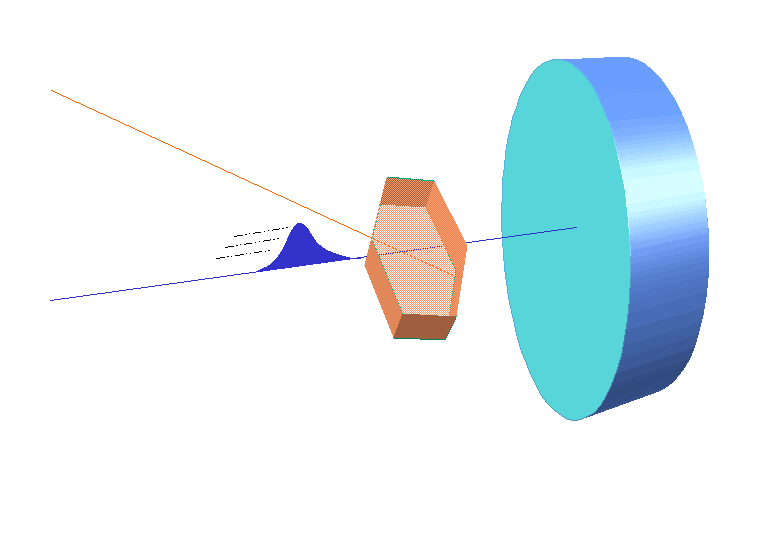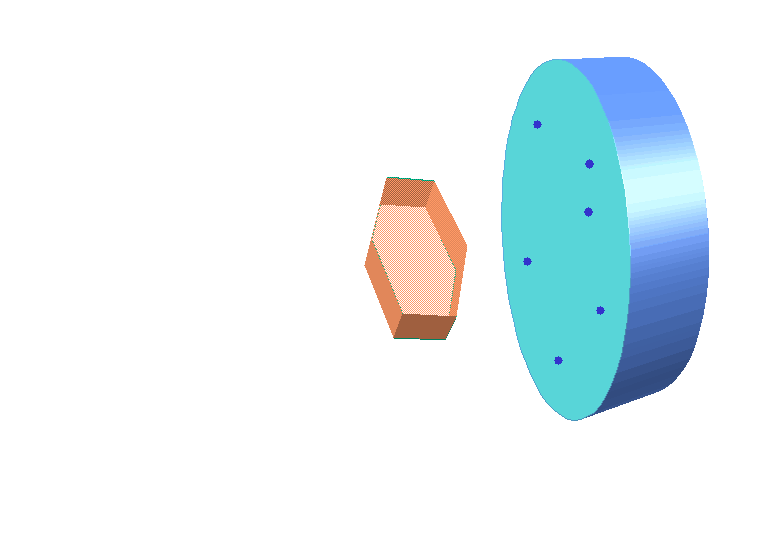W.L. Bragg and his father W.H. Bragg determined the cubic structure of NaCl using X – Rays. According to Bragg, a crystal (Composed of series of equally spaced atomic planes) could be employed not only as a transmission grating (as suggested by Laue) but also as a reflection grating. In Bragg’s treatment, the X – rays strike the crystal at angle q, these penetrates into the crystal and are reflected by different parallel layers of particles in the crystal.
A strong reflected (constructive) beam will result only if all the reflected rays are in phase. The reflected waves by different layer planes will be in phase with one another only if the difference in the path length of the waves reflected from the successive planes is equal to an integral number of wavelengths.
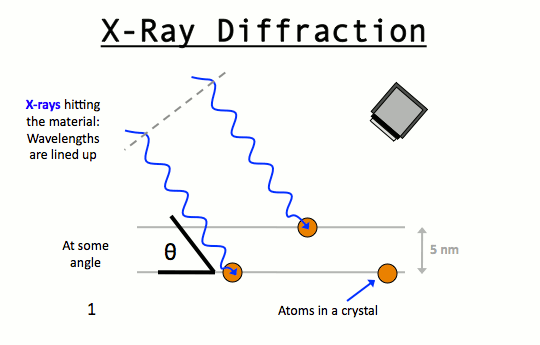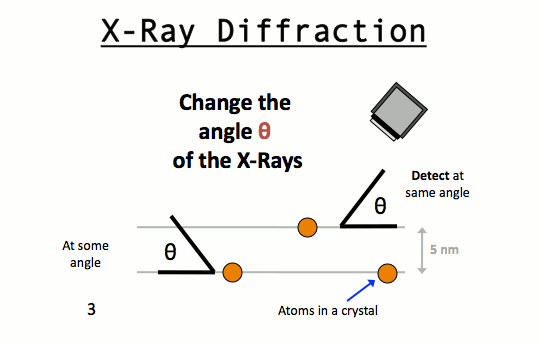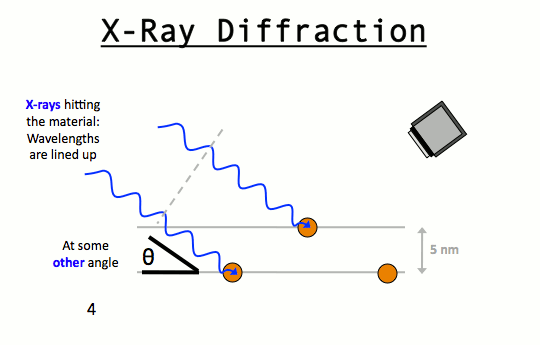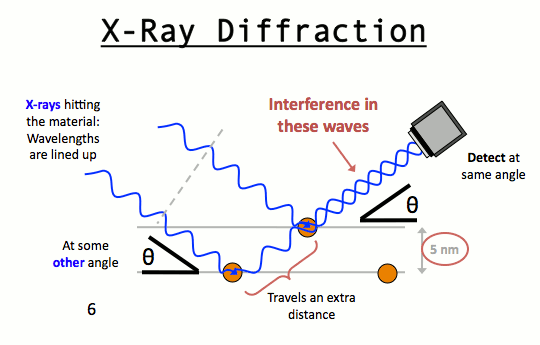
It may noted from the fig. that the beams of X – rays which are reflected from deeper layers travel more to reach the detector. Two X – Ray waves in phase are shown to be approaching the crystal. One wave is reflected from the first layer of atoms while the second wave is reflected from the second layer of atoms. The wave reflected from the second layer travels more distance before emerging from the crystal than the first wave. The extra distance travelled is equal to LN + NM.

For constructive interference to take place the extra distance travelled by the more penetrating beam must be on integral multiple of the wavelength

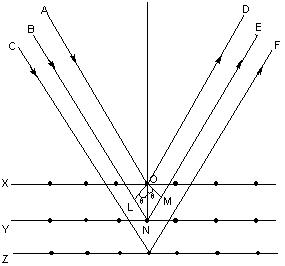Path difference = LN + NM = LN = nγ (n = 1, 2, 3 ….)

Since the triangles OLN and OMN are congruent hence LN = NM

So, path difference = 2LN

LN = d Sinq where d is the distance between two planes

So, path difference = 2d Sinθ

For constructive interference 2 d Sinq must be equal to nl

Or, nγ = 2 d Sinθ

This relation is called Bragg’s equation. Distance between two successive planes d can be calculated form this equation.

With X – Ray of definite wavelength, reflection at various angles will be observed for a given set of planes separated by a distance‘d’.

These reflections correspond to n = 1, 2 , 3 and so on and are spoken of as first order, second order, third order and so on the angle q increases as the intensity of the reflected beams weakens

$x-ray diffraction$

Simple ionic compounds are of two types i.e. AB and AB₂ type.

From the knowledge of close packed structures and the voids developed there in, we can have an idea about the structures of simple ionic compounds.

Among the two ions, constituting the binary compounds, the anions usually constitute the space lattice with hcp or ccp type of arrangements whereas the cations, occupy the interstitial voids

If the anions (B^-) constitute the crystal lattice and all octahedral voids are occupied by cations (A⁺), then the formula of the ionic solid is AB.
Similarly, if half of the tetrahedral voids are occupied by cations, then the formula of the solid crystal becomes A⁺B^-.
When the anions (B^-2) are constituting space lattice and all the tetrahedral voids are occupied by the cations (A⁺), then the formula of the solid crystal will be A₂B.

Ionic Compounds of the type AB

Ionic compounds of the type AB have three types of crystalline structures.

ZnS type
NaCl types
CsCl types

Sodium Chloride (Rock salt) Type Structure

The sodium chloride structure is composed of Na⁺ and Cl^- ions.
The number of sodium ions is equal to that of Cl^- ions. The radii of Na⁺ and Cl^- ions 95 pm and 181 pm giving the radius ratio of 0.524
$\frac{R_{Na^+}}{R_{Cl^-}} = 95 / 181 = 0.524$
The radius ratio of 0.524 for NaCl suggest an octahedral void.
Chloride ions (In a typical unit cell) are arranged in cubic close packing (ccp). In this arrangement, Cl^- ions are present at the corners and at the centre of each face of the cube. This arrangement is also regarded as face centred cubic arrangement (fcc).
The sodium ions are present in all the octahedral holes.
Since, the number of octahedral holes in ccp structure is equal to the number of anions, every octahedral hole is occupied by Na⁺ ions. So that the formula of sodium chloride is NaCl i.e. stoichiometry of NaCl is 1:1.
Since there are six octahedral holes around each chloride ions, each Cl^- ion is surrounded by 6 Na⁺ions. Similarly each Na⁺ ion is surrounded by 6 Cl^- ions. Therefore, the coordination number of Cl^- as well as of Na⁺ ions is six. This is called 6:6 coordination.
It should be noted that Na⁺ ions to exactly fit the octahedral holes, the radius ratio r_NA⁺ / r_Cr should be equal to 0.414. However, the actual radius ratio (r_NA⁺ / r_Cr = 0.524) exceeds this value. Therefore to accommodate large Na⁺ ions, the Cl^- ions move apart slightly i.e. they do not touch each other and form an expanded face centred lattice.
The unit cell of sodium chloride has 4 sodium and 4 chloride ions as calculated below

No of sodium ions = 12 (at edge centres) × 1/4 + 1 (at body centre) × 1= 4

No of chloride ions = 8(at corner) × 1/8+6(at face centres) × 1/2 = 4

Thus, the number of NaCl units per unit cell is 4.

Watch this Video for more reference

Zinc Blende (ZnS) Type Structures (Sphelerite)

The zinc sulphide crystals are composed of equal number of Zn⁺² and S²^- ions.
The radii of the two ions (Zn⁺² = 74 pm and S^-2 = 184 pm) led to the radius (r⁺ / r^–) as 0.40 which suggests a tetrahedral arrangement.
r_Zn⁺² / r_S^–2 = 0.40
The Zinc ions are arranged in ccp arrangement, i.e. sulphide ions are present at the corners and the centres of each face of the cube
Zinc ions occupy tetrahedral hole. Only half of the tetrahedral holes are occupied by Zn⁺² so that the formula of the zinc sulphide is ZnS i.e. the stoichiometry of the compound is 1:1 (Only alternate tetrahedral holes are occupied by Zn⁺²)
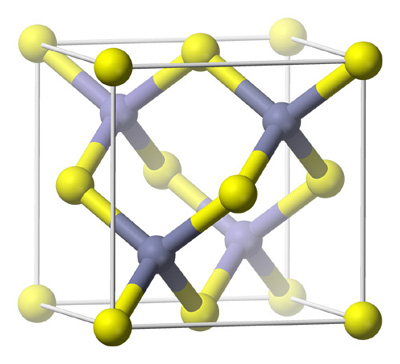Since the void is tetrahedral, each zinc ion is surrounded by four sulphide ions and each sulphide ion is surrounded tetrahedrally by four zinc ions. Thus zinc sulphide has 4:4 Co – ordination.
For exact fitting of Zn^{+2 in the tetrahedral holes, formed by close packing of S-2} ions, the ratio Zn⁺²/S^-2 should be 0.225. Actually this ratio is slightly large (0.40) There are four Zn⁺² ions and four S^-2 ions per unit cell as calculated below:

No. of S^-2 ions = 8(at corners) × 1/8 + 6(at face centres) × 1/2 = 4

No. of Zn⁺² ions = 4(within the body) × 1 = 4

Thus, the number of ZnS units per unit cell is equal to 4. Some more examples of ionic solids having Zinc blende structures are CuC, CuBr, CuI, AgI, beryllium sulphide.

Example

Question:

If silver iodide crystallizes in a zinc blende structure with I^- ions forming the lattice then calculate fraction of the tetrahedral voids occupied by Ag⁺ ions.

Solution:

In AgI, if there are nI^- ions, there will be nAg⁺ ions. As I^- ions form the lattice, number of tetrahedral voids = 2n. As there are nAg⁺ ions to occupy these voids, therefore fraction of tetrahedral voids occupied by Ag⁺ ions = n/2n = ½ = 50%.

The Wurtzite Structures

It is an alternate form in which ZnS occurs in nature.
Sulphide ions have HCP arrangement and zinc ions occupy tetrahedral voids.
Only half the alternate tetrahedral voids are occupied by Zn⁺²ions.
Coordinate no. of Zn⁺² ions as well as S^-² ions is 4. Thus, this structure has 4 : 4 coordination.
No. of Zn⁺² ions per unit cell = 4(within the unit cell) × 1 + 6(at edge centres) × 1/3 = 6
No. of S^-² ions per unit cell = 12(at corners) × 1/6 + 2 (at face centres) × 1/2 + 3 (within the unit cell) × 1 = 6
Thus, there are 6 formula units per unit cell.

Caesium Chloride (CsCl) Structure

The caesium chloride crystal is composed of equal number of caesium (Cs⁺) and Chloride Cl^-ions. The radii of two ions (Cs⁺ = 169 pm and Cl^- = 181 pm) led to radius ratio of r_CS⁺ to r_Cl^– as 0.93 which suggest a body centred cubic structure having a cubic hole
R_CS⁺ to R_Cl^– = 169 / 181 = 0.93
The chloride ion form the simple cubic arrangement and the caesium ions occupy the cubic interstitial holes. In other words Cl^- ions are at the corners of a cube whereas Cs⁺ ion is at the centre of the cube or vice versa .
Each Cs⁺ ion is surrounded by 8 Cl^- ions and each Cl^- ion in surrounded by 8 Cs⁺ ions. Thus the Co – ordination number of each ion is eight.
For exact fitting of Cs⁺ ions in the cubic voids the ratio r_CS⁺ / r_Cl^– should be equal to 0.732. However, actually the ratio is slightly larger (0.93). Therefore packing of Cl^- ions slightly open up to accommodate Cs⁺ ions.
The unit cell of caesium chloride has one Cs⁺ ion and one Cl^- ion as calculated below

No. of Cl^- ion 8(at corners) × 1/8 = 1

No. of Cs⁺ ion = 1(at body centre) × 1=1

Thus, number of CsCl units per unit cell is 1

Relation between radius of cation and anion and edge length of the cube, r_CS to r_Cl = a√3/2

Other common examples of this type of structure are CsBr, CsI, TlCl, TlBr

Higher coordination number in CsCl(8:8) suggest that the caesium chloride lattice is more stable than the sodium chloride lattice in which Co – ordination number is 6:6. Actually the caesium chloride lattice is found to be 1% more stable than the sodium chloride lattice. Then the question arises why NaCl and other similar compounds do not have CsCl type lattice – This is due to their smaller radius ratio. Any attempt to pack 8 anions around the relatively small cation (Li⁺, Na⁺, K⁺, Rb⁺) will produce a state in which negative ions will touch each other, sooner they approach a positive ion. This causes unstability to the lattice.

Ionic compound of AB₂ type

Fluorite Structures

The Ca⁺² ions are arranged in ccp arrangement, i.e. these ions occupy all the corners and the centres of each face of the cube
The F^– ions occupy all the tetrahedral holes.
Since there are two tetrahedral holes for each Ca⁺² ion and F^- ions occupy all the tetrahedral holes, there will be two F^- ions for each Ca⁺² ions, thus the stoichiometry of the compound is 1:2.
Each Ca⁺² ion is surrounded by 8F^- ions and each F^-ions is surrounded by 4Ca⁺² ions. The Coordination number of Ca⁺² ion is eight and that of F^- ion is four, this is called 8:4 Coordination.
Each unit cell has 4 calcium ions and 8 fluoride ions as explained below

No. of Ca⁺² ions = 8(at corners)×1/8 + 6 (at face centres)´1/2

No. of F ions = 8 (within the body)×1 = 8

Thus the number of CaF₂ units per unit cell is 4.

Other examples of structure are SrF₂, BaCl₂, BaF₂, PbF₂, CdF₂, HgF₂, CuF₂, SrCl₂, etc.

Ionic compound of A₂B type

Anti-Fluorite Structure

The compound having A₂B formula are compounds having anti fluorite structure
Anti fluorite structure is having arrangement of cations and anions opposite to the fluorite structure Li₂O has an anti fluorite structure.
In the crystal structure of Li₂O, the O^-2 ions constitute a cubic close packed lattice (fcc structure) and the Li⁺ ions occupy all the tetrahedral voids
Each oxide ion, O^-2 ion is in contact with 8 Li⁺ ions and each Li⁺ ions having contact with 4 oxide ion. Therefore, Li₂O has 4:8 coordination
Examples – Na₂O, K₂O, K₂S, Na₂S, Rb₂O, Rb₂S

Corundum Structure

The general formula of compounds crystallizing in corundum structure is A₂O₃^.
The closest packing is that of anions (oxide) in hexagonal primitive lattice and two-third of the octahedral voids are filled with trivalent cations. Examples are : Fe₂O₃, Al₂O₃ and Cr₂O₃.

Pervoskite Structure

The general formula is ABO₃. One of the cation is bivalent and the other is tetravalent.
Example: CaTiO₃, BaTiO₃. The bivalent ions are present in primitive cubic lattice with oxide ions on the centers of all the six square faces.
The tetravalent cation is in the center of the unit cell occupying octahedral void.

Spinel and Inverse Spinel Structure

Spinel is a mineral (MgAl₂O₄). Generally they can be represented as M²⁺M₂³⁺O₄, where M²⁺ is present in one-eighth of tetrahedral voids in a FCC lattice of oxide ions and M³⁺ ions are present in half of the octahedral voids. M²⁺ is usually Mg, Fe, Co, Ni, Zn and Mn; M³⁺ is generally Al, Fe, Mn, Cr and Rh.
Examples are ZnAl₂O₄^, Fe₃O₄^,FeCr₂O₄ etc.
Many substances of the type M⁴⁺M₂²⁺O₄also have this structure. In an inverse spinel the ccp is of oxide ions, M²⁺ is in one-eight of the tetrahedral voids while M³⁺ would be in one-eight of the tetrahedral voids and one-fourth of the octahedral voids.

Crystal structure		Brief description	Coordination number	No. of atoms per unit cell	Examples
1.	Rock salt (NaCl – type)	Cl^- ions in ccp Na⁺ ions occupy all octahedral voids	Na⁺ = 6 Cl^- = 6	4	Li, Na, KI, and Rb halides NH₄Cl, NH₄Br, NH₄I, AgF, AgCl, AgBr, MgO, CaO, TiO, FeO, NiO
2.	Zinc blende (ZnS – types)	S^-2 ions in ccp Zn⁺² ions occupy alternate tetrahedral voids	Zn⁺² = 4 S^-2 = 4	4	ZnS, BeS, CuCl, CuBr, CuI, AgI, HgS
3.	Wurtzite (ZnS – type)	S^-2 ions in hcp Zn⁺² ion occupy alternate tetrahedral voids	Zn⁺² = 4 S^-2 = 4	4	ZnS, ZnO, CdS, BeO
4.	Caesium chloride (CsCl type)	Cl^- ions in bcc Cs⁺ ions in the body of cube	Cs⁺² = 8 Cl^- = 4	1	CsCl, CsBr, CsI, CsCN,CaS
5.	Fluorite (CaF₂type)	Ca⁺² ions in ccp, F^- ions occupy all tetrahedral voids	Ca⁺² = 8 F^- = 4	4	CaF₂, SrF₂, BaF₂, BaCl₂, SrCl₂, CdF₂, HgF₂
6.	Anti fluorite (Li₂O – type)	O^-2 ions in ccp, Li⁺ ions occupy all tetrahedral sites	Li⁺ = 4 O^-2 = 8	4	K₂O, Na₂O, K₂S, Na₂S

Question 1: The ratio of radii of Na⁺ and Cl^- ions n rock salt structure is

a. 0.524

b. 0.453

c. 0.562

d. 0.842

Question 2: In zinc blende structure r_Zn⁺² / r_S^–2

a. 0.62

b. 0.40

c. 0.82

d. 0.71

Question 3: Which of the following molecules does not have caesium chloride structure?

a. CsBr

b. CsI

c. TlCl

d. CaF

Question 4: The unit cell of caesium chloride has one Cs⁺ ion and

a. one Cl^-

b. two Cl^-

c. three Cl^-

d. four Cl^-

Question 5: The general formula of compounds crystallizing in corundum structure is ^.

a. AO₃

b. A₂O

c. A₂O₂

d. A₂O₃

Q.1	Q.2	Q.3	Q.4	Q.5
a	b	d	a	d

Related Resources

You can also refer to Syllabus of IIT JEE
Look here for Past year Papers of IIT JEE
Click here to refer Crystal Lattices and Unit Cells

To read more, Buy study materials of Solid State comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.