Sum to n terms of Special Series

 

Table of contents

Meaning of Series Types of Series Arithmetic Series Geometric Series Special Series Sum to n terms of Special Series

Meaning of Series

The sum of all the numbers of the given sequence is called Series. It could be finite or infinite, like the sequences. It is written as S_n.

Example

If the given sequence is 1, 3, 5, 7, …

Then the series will be 1 + 3 + 5 + 7 + …

And we will write it as

S_n = 1 + 3 + 5 + 7 + …
 

Types of Series

The different types of series are:
 

Arithmetic Series

The Arithmetic series is basically the sum of the terms of the arithmetic sequence that is, if the difference between the every successive term to its preceding term is always constant then it is said to be an arithmetic series.

Here we can see that we are getting the next term by adding the constant term that is, 3. So the first term is a = 2 and the common difference is d = 3.

The arithmetic series can be written in the form of

{a + (a + d) + (a + 2d) + (a + 3d) + .........}

where a is the first term of the series and d is the difference of it which is known as the Common Difference of the given series.

Formula of nth term of the Arithmetic Series

if we know that

a is the first term,

d is the difference and

n is the total number of the terms,

then the formula for the nth term will be

a_n = a + (n - 1) d
 

Sum of an Arithmetic Series

This is the arithmetic series with a = 1 , d = 1 and n = 5

Let’s find its sum with the formula

Example

Solve the Arithmetic Series to find the sum of the first 5 terms of the series.

Solution:

Given

a = 6 (first term of the series)

d = 2 ( common difference between the terms)

n = 5

By putting the values in the formula

 

Geometric Series

The Geometric Series is basically the sum of the terms of the Geometric sequence that is, if the ratio between the every successive term to its preceding term is always constant then it is said to be a Geometric series.

Here we are getting the next term by multiplying a constant term that is, 1/2. So the first term is a = 1/2 and the common ratio is r = 1/2

Formula of nth term of the geometric series

In general, the geometric series is in the form of

Where, a is the first term of the series and r is the common ratio for it.

Formula for nth term of the geometric series

a_n = a₁ r ^{n - 1} 

Where, n is the number of the term.

Sum of geometric series

Example

What is the sum of the series

Solution:

First we have to check whether it is an arithmetic series or geometric series. As we can see that this is a geometric series because the ratio between every successive term is constant.

a = 2 , r =  and n = 5

By putting the values, in the formula of the sum of the G.P.

Special Series

Special Series are the series which are special in some way. It could be arithmetic or geometric.

Some of the special series are:

(i) 1 + 2 + 3 +… + n (sum of first n natural numbers)

(ii) 1² + 2² + 3² +… + n²(sum of squares of the first n natural numbers) 

(iii) 1³ + 2³ + 3³ +… + n³(sum of cubes of the first n natural numbers). 

Sum to n terms of Special Series

Let’s try to find the formula to find the sum of the above special series-

(i) S_n = 1 + 2 + 3 + 4 +… + n

Here we have to find the sum of the first n natural numbers.

This is an arithmetic progression as we can see

a = 1 and d = 1

The formula of the sum of the A.P. is

(ii) S_n = 1² + 2² + 3² +… + n²

Here we consider the identity

k³ - (k-1)³ = 3k² - 3k +1

If we take the value of k as, k = 1, 2…, n    

We get

1³ – 0³ = 3 (1)² – 3 (1) + 1

2³ – 1³ = 3 (2)² – 3 (2) + 1

3³ – 2³ = 3(3)² – 3 (3) + 1

 .......................................

.......................................

......................................

n³ – (n – 1)³ = 3 (n)² – 3 (n) + 1 

Now by adding both sides, we get

n³ – 0³ = 3 (1² + 2² + 3² + ... + n²) – 3 (1 + 2 + 3 + ... + n) + n

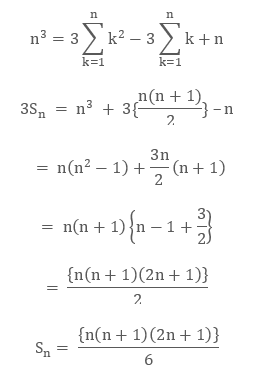
(iii) S_n = 1³ + 2³ + 3³ +… + n³

Here we consider the identity,

(k + 1)⁴ – k⁴ = 4k³ + 6k² + 4k + 1

Now we will put the values of k as k = 1, 2, 3… n,

Then we get

2⁴ – 1⁴ = 4(1)³ + 6(1)² + 4(1) + 1

3₄ – 2₄ = 4(2)₃ + 6(2)₂ + 4(2) + 1

4⁴ – 3⁴ = 4(3)³ + 6(3)² + 4(3) + 1

 ..................................................

..................................................

..................................................

(n – 1)⁴ – (n – 2)⁴ = 4(n – 2)³ + 6(n – 2)² + 4(n – 2) + 1

n⁴ – (n – 1)⁴ = 4(n – 1)³ + 6(n – 1)² + 4(n – 1) + 1

(n + 1)⁴ – n⁴ = 4n³ + 6n² + 4n + 1

Now add both sides,

We get

(n + 1)⁴ – 1⁴ = 4(1³ + 2³ + 3³ +...+ n³) + 6(1² + 2² + 3² + ...+ n²) + 4(1 + 2 + 3 +...+ n) + n

Finally, we get the formulas for the above three special series.

Example

Find the sum of first n terms of the series 1.3 + 3.5 + 5.7 + ...

Solution:

Let S_n = 1.3 + 3.5 + 5.7 + ...

Here the n th term of the series

t _n = {n th term of 1, 3, 5, ...} × {n th term of 3, 5, 7,...}

= (2n – 1) (2n + 1) = 4n² – 1 

Example

Find the sum to n terms of the series 3 + 7 + 13 + 21 + 31 +…

Solution:

Let S = 3 + 7 + 13 + 21 + 31 +……..+ a_n-1 + a_n

S = 3 + 7 + 13 + 21 + 31+… + a_n-2 + a_n-1 + a_n

By subtracting the two equations , we get

More Readings

Sum to n terms of Special Series