Series

 

Table of contents

Meaning of Series History of Series Notation of Series Difference between Sequence and Series Finite and Infinite Series Convergent and Divergent Series Comparison test Properties of Series Non Negative term Absolute Convergence Conditional Convergence Types of Series Arithmetic Series Geometric Series Harmonic Series Alternating Harmonic Series Fibonacci Series

Meaning of Series

Series is the sum of all the numbers of the sequence. Generally it is written as S_n.

Example

If we have a sequence 1, 2, 3, 4, …

Then the series of this sequence is 1 + 2 + 3 + 4 +…
 

History of Series

The first known summation of an infinite series was produced by Greek mathematician Archimedes which is still used in the area of calculus today.

Mathematicians from Kerala, India studied infinite series in around 1350 CE. 

Notation of Series

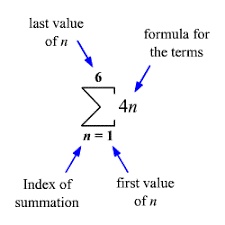
We use the sigma notation that is, the Greek symbol “Σ” for the series which means “sum up”.

The series 4+8+12+16+20+24 can be expressed as ∑⁶_{n = 1} = 4n. We read this expression as the sum of 4n as n goes from 1 to 6.

This is the compact form of the series so we can generate the terms of the series by the formula easily.

To generate the terms of the series given in sigma notation above we have to replace the n with 1, 2,3,4,5 and 6 as the last number of term is 6.

Difference between Sequence and Series

Sequence	Series
It is an ordered list of numbers.	It is the value which we get by adding up the terms of the sequences.
Its notation is	Its notation is
Example 2, 4, 6, 8,…	Example 2 + 4 + 6 + 8 + …

Finite and Infinite Series

A series which have a limited number of terms is called Finite Series.

2 + 4 + 6 + 8 + 10

A series which have unlimited number of terms is called Infinite Series.
 

Convergent and Divergent Series

If we have a sum of a series which is approaching towards a finite value is called a Convergent Series. And if a sum does not converge then it is called divergent series.

A series ∑a_n is said to converge or to be convergent when the sequence (s_k) of partial sums has a finite limit. If the limit of s_k is infinite or does not exist, the series is said to diverge.

Example

Find whether the series is convergent or divergent.

Here the sum of the series would be

But if this is not true then it would be  a divergent series.
 

Comparison test

This is the test to check whether a series is convergent or divergent.

Let us take two series

where, a_n, b_n ≥ 0

and a_n ≤ b_n  for all n =1, 2, 3 …

This tells us that these series are either diverges to positive infinity or they are going to converge to finite value.

that is, if the larger series converges then the smaller series also converges.

that is, if the smaller series diverges then the larger series also diverges.

Properties of Series

The series are not only differentiated by their convergence or divergence but also by the properties of the term a_n .

Non Negative term

When a_n is a non-negative real number for every n, the sequence S_N of partial sums is non-decreasing. It follows that a series ∑a_n with non-negative terms converges if and only if the sequence S_N of partial sums is bounded.

is convergent, because of the inequality

and a telescopic sum argument implies that the partial sums are bounded by 2.

Absolute Convergence

A series

is said to converge absolutely if the series of absolute values

converges. This is sufficient to guarantee not only that the original series converges to a limit, but also that any reordering of it converges to the same limit.

Conditional Convergence

A series of real or complex numbers is said to be conditionally convergent (or semi-convergent) if it is convergent but not absolutely convergent. A famous example is the alternating series

which is convergent, but the series formed by taking the absolute value of each term is the divergent harmonic series.

Types of Series

There are different types of series:
 

Arithmetic Series

The summation of the terms of the arithmetic sequence is the arithmetic series that is, if the difference between the every term to the next term is always constant then it is said to be an arithmetic series.

The arithmetic series is in the form of

{a + (a + d) + (a + 2d) + (a + 3d) + .........}

where a is the first term of the series and d is the difference of it which is known as the common difference of the given series.
 

Formula of Arithmetic Series

if a is the first term, d is the difference and n is the total number of the terms, then the formula for nth term is given by

a_n = a + (n - 1) d

Sum of an Arithmetic Series 

S_n = n/2 [2a + (n - 1) d]

Example

Find the sum of the first ten terms of the given arithmetic series.

Solution: Given

a = 10 (first term)

d = 2 ( common difference)

n = 10 ( as we need to calculate the sum of the first ten terms of the series)

Now we will put the values in the formula

Geometric Series

The summation of the terms of the geometric sequence is the geometric series that is, if the ratio between the every term to the next term is always constant then it is said to be a geometric series.

Formula of Geometric Series

In general, we can define geometric series as:

Where, a is the first term of the series and r is the common ratio for it.

Formula for nth term of the geometric series

a_n = a₁ r ^{n - 1} 

Where, n is the number of the term.

Sum of Geometric Series

Convergent Geometric Series

If the value of the common ratio r lies in between 0 and 1 or IrI < 1, then the geometric series is said to be convergent.

And, if the value of r ≥ 1, then the series is diverges.

Example 1

How can we get answer 1 of an infinite series?

Solution: Let’s solve it using Algebra:

Let

Now multiply S by ½

Now subtract them!

All the terms from 1/4 onwards will be cancelled out.

And we get: S - S/2 = 1/2  

Simplify: S/2 = 1/2

Hence: S = 1

Example 2

Find the sum of the finite geometric series

Solution: To find the sum of the series first we need to expand the series.

So we can see that

a = 2

r = 3

n = 100 

So we will put the values in the formula of the sum of the geometric series

Example 3

Find the sum of infinite geometric series.

Solution:  Given r = 1/3

So we can rewrite the equation as:

The summation of the series would be 

Now the formula for the infinite geometric series is

This is going to converge if │r���<1

Harmonic Series

Harmonic series is the reciprocal of Arithmetic series. It is in the form of

It is just the infinite sum of the harmonic sequence.

There is no special formula for finding the sum of the harmonic series so we can calculate the sum of the arithmetic series and then take the reciprocal of it which will be the sum of the harmonic series.

The harmonic series is divergent to infinity.

Alternating Harmonic Series

The formula for the alternating harmonic series is

This is conditionally convergent series to natural logarithm to 2
 

Fibonacci Series

Fibonacci series is the sum of Fibonacci sequence. It is the series of the numbers in which we get the next number by adding the two numbers before it.

Example

2 + 2 + 4 + 6 + 10 +…

Formula of Fibonacci Series

If x_n is the n^th term, x_n-1 is the (n – 1)^th term and x_{n - 2} is the n - 2^nd term of any Fibonacci series, then we have a formula for it as x_n = x_n-1 + x_n-2

More Readings

Series