Friction

 

Table of Content

Cause of Friction Types of Friction Cause and Direction of Rolling Friction Co-Efficient of Friction Angle of Friction Angle of Repose Methods of Reducing Friction Related Resources

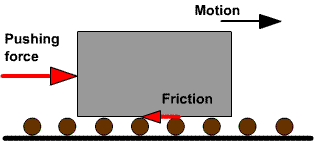Whenever the surface of a body slides over another, each body experiences a contact force which always opposes the relative motion between the surfaces. This contact force is called frictional force. Intermolecular interaction arising due to elastic properties of matter is the cause of frictional force.This force acts tangentially to the interface of two bodies.

Cause of Friction

Old view:-

Earlier it was thought that roughness of the two surfaces causes friction in the figure because it can be easily seen that smoother the surfaces, lesser is the friction. Interlocking of irregularities of the two surfaces causes hindrance to sliding. This, however, is not the current view.

Current view:-

The current view is a slight deviation from the old view. Earlier we thought that interlocking of irregularities of surfaces was causing friction. Now, it is though that due to irregularities, the common surface area which is in actual contact of the two surfaces, is much less than the total overall area in contact. In one experiment, it came out to be 1/10,000^th of the apparent area.

Thus, while the total interactive (action and reaction) forces between the two surfaces remain the same, the pressures at the points of contact are extremely high and cause the humps to flatten out (undergoing plastic deformation) until the increased area of contact enables the upper solid to be supported. It is thought that at the points of contact, small, cold-welded joints are formed by the strong adhesive forces between molecules which are very close together. These have to be broken away before one surface can move over the other. Thus the force of friction is found to depend upon the following factors.

(i) The nature of two surfaces with the surfaces are being pressed together.

(ii) Normal force with the surfaces are being pressed together.

(iii) Actual area of contact

Types of Friction

There are four types of friction.

(a) Static Friction   (b) Kinetic Friction     (c) Rolling Friction      (d) Fluid Friction

(a)Static friction:- 

Static friction is the force of friction between two surfaces so long as there is no relative motion between them. It is always equal to the applied force. The static frictional forces are incorporated in the following inequality.

The magnitude of static friction f_s (static frictional force) has a maximum value f_s,max  that is given by,

f_s,max  = µ_sN

Here µ_s is the coefficient of kinetic friction and N is the normal force.

So, coefficient of static friction, µ_s= f_s,max /N

Static friction is always equal to the apllied force. It will be observe that value of static friction increases to certain maximum value, beyond which if the applied force is increased body starts moving. This maximum value of force of friction is called limiting friction.

Limiting friction is the maximum value of force of friction between two surfaces so long as there is no relative motion between them.

(b) Kinetic friction:- 

Kinetic friction is the force of friction which comes into play between two surfaces when there is some relative motion between them. The magnitude of force of kinetic friction f_k (kinetic frictional force) is proportional to the normal force N.

So,

 

Here µ_k is the coefficient of kinetic friction.

Thus, coefficient of kinetic friction, µ_k = f_k/N  

Laws of limiting friction:-

(a) The direction of force of friction is always opposite to the direction of motion.

(b) The force of limiting friction depends upon the nature and state of polish of the surfaces in contact and acts tangentially to the interface between the two surfaces.

(c) The magnitude of limiting friction ‘F’ is directly proportional to the magnitude of the normal reaction R between the two surfaces in contact, i.e.,

F∝R

(d) The magnitude of the limiting friction between two surfaces is independent of the area and shape of the surfaces in contact so long as the normal reaction remains the same.

(c) Rolling friction:-

 Force of friction which comes into play, between two surfaces, while one is rolling over the other is called rolling friction.  Rolling friction is similar to kinetic friction.

So, 

Here µ_r is the coefficient of rolling friction and N is the normal force.

(d) Fluid friction:-

Fluid friction is the opposing force which comes into play when a body moves through a fluid.

Cause and Direction of Rolling Friction

A wheel of radius R rolling without sliding on a flat surface will experience a resistance due to the very small local deformation that takes place, which is sometimes elastic sometimes inelastic, i.e., a kind of ridge is formed in front of the wheel as shown exaggerated in the figure. This gives rise to the force F_R, whose line of action passes through the center C of the wheel and P the horizontal force necessary to force the wheel to topple over the point M, the total clockwise torque acting on the wheel about M must be more than or marginally more than the total anticlockwise torque about M.

 F = Frictional force

Therefore,

P × R cos θ > mg × R sin θ

P > mg tan θ

The value of "tan θ" is called the coefficient of rolling friction (μ_g). This value does not depend upon R. If the two surfaces are absolutely rigid, then no ridge will be formed and q will be zero i.e., coefficient of rolling friction will be zero.

Typical values are μ_R = 0.006 for steel and 0.02 - 0.04 for rubber tiers on concrete surfaces. Rolling friction is very small compared to the sliding friction. In case of pure rolling μ_R = 0.

The value of angle of friction and that of angle of repose are same and the tangents of both of them is equal to the co-efficient of friction. When a body slides down an inclined plane, whose angle of inclination with the horizontal is equal to angle of repose, it moves with uniform velocity. Sliding friction and rolling friction are independent of velocity. Fluid friction depends upon velocity. It increases with an increase in velocity. Force of limiting friction does not depend upon the size and shape of surface in contact. Coefficient of kinetic friction is less than coefficient of static friction i.e.,µk ?µs

Co-Efficient of Friction

According to the law of limiting friction,

F ∝  R

Or F = μR           ............ (1)

where μ is a constant of proportionality and is called the coefficient of limiting friction between the two surfaces in contact.

From (1),

Hence coefficient of limiting friction between any two surfaces in contact is defined as the ratio of the force of limiting friction and normal reaction between them. The value of μ depends on

(i) nature of the surfaces in contact i.e., whether dry or wet; rough or smooth; polished or not polished.

(ii) material of the surfaces in contact.

 For example, when two polished metal surfaces are in contact, μ ≈ 0.2, when these surfaces are lubricated, μ ≈ 0.1. Between two smooth wooden surfaces, μ varies between 0.2 and 0.5. Obviously, μ has no units.

 When a body is actually moving over the surface of another body, we place F by F_x, the kinetic friction, and μ and μ_k.

Therefore,

 μ_k is then called the coefficient of kinetic or dynamic friction. As F_k < F, therefore, μ_k is always less than μ i.e. coefficient of kinetic or dynamic friction is always less than the coefficient of limiting friction.

Table gives the values of coefficient of limiting/kinetic friction between some pairs of materials:

S.No.	Surface in contact	Coefficient of limiting friction	Coefficient of kinetic friction
1.	Wood on wood	0.70	0.40
2.	Wood on leather	0.50	0.40
3.	Steel on Steel (mild)	0.74	0.57
4.	Steel on Steel (hard)	0.78	0.42
5.	Steel on Steel (greased)	0.10	0.05

Angle of Friction

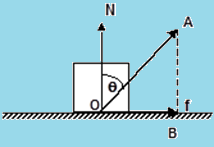
The angle made by the resultant reaction force with the vertical (normal reaction) is known as the angle of the friction.

  Now,  in the triangle OAB,

AB/OB = cotθ

So, OB = AB/ cotθ

            = AB tanθ

Or, tanθ = OB/AB

              = f / N

So, tanθ = f / N  = µ_s

Angle of Repose

It is the angle which an inclined plane makes with the horizontal so that a body placed over it just begins to slide of its own accord.

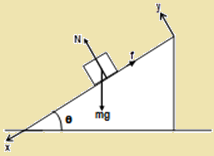Consider a body of mass m resting on an inclined plane of inclination θ . The forces acting on the body are shown – F_f being the force of friction. If friction is large enough, the body will not slide down.

Along x: mg sin θ – f = 0          

Along y: N –mg cosθ = 0                

 i.e. N = mg cos θ and f = mg sin θ 

Thus, f ≤ µ_sN  gives,

mg sin θ ≤ µ_s mg cosθ 

So, tan θ ≤ µ_s. This signifies, the coefficient of static friction between the two surfaces, in order that the body doesn’t slide down.

When θ is increased, then  tan θ >  µ . Thus sliding begins, and the angle θ_r = tan^-1µ. This angle is known as the angle of repose.

To know about friction, please refer this video:-

Methods of Reducing Friction

Friction can be reduced if we try to remove the cause of friction.

(a) By rubbing and polishing

(b) By lubricants

(c) By converting sliding into rolling friction

(d) By streamlining

Problem:-

A horizontal bar is used to support a 75-kg object between two walls, as shown in the below figure. The equal forces F exerted by the bar against the walls can be varied by adjusting the length of the bar. Only friction between the ends of the bar and the walls supports the system. The coefficient of static friction between bar and walls is 0.41. Find the minimum value of the forces F for the system to remain at rest.

Concept:-

The diagram below shows the forces involved in the system:

The magnitude of frictional force between the walls and the bar is,

f = µ_sN

Here  µ_s is the coefficient of static friction between the walls and the bar , and N is the normal force exerted by the wall on the bar.

If the bar is at rest, the horizontal equilibrium is maintained and the sum of the horizontal forces on the bar must be zero, that is

F – N = 0

F = N

Substitute F = N in equation f = µ_sN ,

f = µ_sN

  =µ_s F

 

f + f – W = 0

f + f = W

2f = W

It is important to note that the term on the left hand side of the above equation account for the fact that the frictional force exist at both the ends of the bar and acts in a direction opposite to the direction of weight.

W = mg

Substitute W = mg and f = µ_sF  in equation 2f = W,

2f = W

2(µ_sF) = W

F = mg/2µ_s

This equation can be used to calculate the magnitude of force exerted by the bar on the wall that will balance the system.

To calculate the magnitude of force F, substitute 75 kg for m , 9.81 m/s² for g and 0.41 for µ_s in equation F = mg/2µ_s ,

F = mg/2µ_s

  = (75 kg) (9.81 m/s²)/2(0.41)

 = (897.2 kg.m/s²) (1 N/1 kg.m/s²)

= 897.2 N

Round off to two significant figures,

F= 897.2 N

Therefore, the magnitude of the force exerted by the bar on the wall, to balance the system is 897.2 N.

Question 1:-

If a surface is smoothened, how will it affect the angle of friction:

(a) it will decrease                        (b) it will increase

(c) proportional to each other      (d) none

Question 2:-

Angle of friction and angle of repose are:

(a) equal to each other                            (b) not equal to each other

(c) proportional to each other                 (d) none

Question 3:-

Which is a suitable method to decrease friction:

(a) ball and roller bearing                    (b) lubrication

(c) polishing                                            (d) all of the above

Question 4:-

Friction can be:

(a) completely avoided                       (b) minimized

(c) cannot be minimized                   (d) of conservative nature

Question 5:-

If the normal reaction is doubled, what happens to the co-efficient of friction between the two surfaces:

(a) it is doubled                            (b) it is halved

(c) it remains unchanged           (d) none of the above

Q.1	Q.2	Q.3	Q.4	Q.5
a	a	d	b	c

Related Resources

• You might like to refer Collision.

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

To read more, Buy study material of Laws of Motion comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here.