Guest

Self Study Packages
Resources
Ask a Question
NRI Section
- UAE
  - UAE
  - Dubai
  - Sharjah
  - Abu Dhabi
- Saudi Arabia
  - Saudi Arabia
  - Jeddah
  - Riyadh
  - Dammam
  - Al Jubail
- Qatar
  - Qatar
  - Doha
- Oman
  - Oman
  - Muscat
  - Salalah
- Bahrain
  - Bahrain
  - Manama
- Kuwait
  - Kuwait
  - Mahboula
  - Salmiya
- Indonesia
- Malaysia
- Singapore
- Uganda
- USA
- View complete NRI Section
Notes
- Study Material (JEE/NEET)
- Study Notes (JEE/NEET)
More
- Study Center
- Blog

Circular Motion

Table of Content

Direction of Motion of Body at any Instant
Relation Between these Parameters
Simulation for Circular Motion’s Component
Related Resources

A Particle Moving in a Circular Path

Now we shall discuss another example of two-dimensional motion that is motion of a particle on a circular path. This type of motion is called circular motion.The motion of a body is said to be circular if it moves in such a way that its distance from a certain fixed point always remains the same.

Direction of Motion of Body at any Instant

If the string breaks suddenly, the stone shall fly tangentially to the path of motion. So, instantaneous direction of motion of the body is always along the tangent to the curve at that point.

Consider a particle P is moving on circle of radius r on X-Y plane with origin O as centre.

The position of the particle at a given instant may be described by angle θ, called angular position of the particle, measured in radian. As the particle moves on the path, its angular position θ changes. The rate of change of angular position is called angular velocity, ω, measured in radian per second.

$\omega = \lim_{\Delta t \to 0}\frac{\Delta \theta }{\Delta t}$

= dθ/dt = ds/rdt = v/r

The rate of change of angular velocity is called angular acceleration, measured in rad/s². Thus, the angular acceleration is

α = dω/dt = d²θ/dt²

Relation Between these Parameters

Particle P is Moving on Circle of Radius r on X-Y Plane

It is easy to derive the equations of rotational kinematics for the case of constant angular acceleration with fixed axis of rotation. These equations are of the same form as those for on-dimensional transitional motion.

ω = ω₀ + αt ............ (a)

? = ?₀ + ω₀t + αt²/2 ............ (b)

ω² = ω₀2 + 2α (? - ?₀) ............ (c)

? = ?₀ + (ω₀ + ω)/(2t) ............ (d)

Here, ?₀ is the initial angle and ω₀ is the initial angular speed.

Problem 1:

(a) What is the angular velocity of the minute and hour hands of a clock?

(b) Suppose the clock starts malfunctioning at 7 AM which decelerates the minute hand at the rate of 4Π radians/day. How much time would the clock loose by 7 AM next day?

Solution:-

(a) Angular speed of,

minute hand : ω_mh = 2π rad/hr = 48π rad/day = (Π/1800) rad/sec

hour hand : ω_hh = (π/6) rad/hr = 4π rad/day = (Π/21600) rad/sec

(b) Assume at t = 0, ?₀ = 0, when the clock begins to malfunction.

Use equation (ii) to get the angle covered by the minute hand in one day.

So, ? = ω₀(1 day) 1/2α(1 day)² = 46π rad

Hence the minute hand complete 23 revolutions, so the clock losses 1 hour.

Problem 2:

A particle is rotating in a circular path having initial angular velocity 5 rad/sec and the angular acceleration α = 0.5 ω, where ω is angular velocity at that instant. Find the angular velocity, after it moved an angle π?

Solution:-

Here angular acceleration is

α = 0.5 ω

=> dω/dt = 0.5ω

=> (dω/dθ) (dθ/dt) = 0.5ω

=> ω dω/dθ = 0.5ω

Or,

$\int_{5}^{\omega }d\omega =0.5\int_{0}^{\Pi }d\theta$

=> ω - 5 = 0.5 × π

=> ω = 5 + 0.5 ×π = 6.57 rad/sec.

Hence, when acceleration is not constant, use the method of calculus as shown in above illustration.

Simulation for Circular Motion’s Component

This animations shows the vectors components for any object traveling in a circle. (Radius vector, velocity vector, centripetal force vector and centripetal acceleration vector.) It then animates them traveling in a circle.

Motion of a Particle in a Circular Path

Motion of a Particle in a Circular Path It is a special kind of two-dimensional motion in which the particle's position vector always lies on the circumference of a circle. In order to calculate the acceleration parameter it is helpful to first consider circular motion with constant speed, called uniform circular motion. Let there be a particle moving along a circle of radius r with a velocity $\vec{v}$ , as shown in figure given below, such that $\left | \vec{v} \right |$ = v = constant. For this particle, it is our aim to calculate the magnitude and direction of its acceleration. We know that,

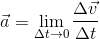
$\vec{a} =\lim_{\Delta t \to 0}\frac{\Delta \vec{v}}{\Delta t}$

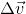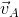Now, we have to find an expression for $\Delta \vec{v}$ in terms of known quantities. For this, consider the particle velocity vector at two points A and B. Displacing $\vec{v_{B}}$ , parallel to itself and placing it back to back with $\vec{v_{A}}$ , as shown in figure given below. We have

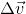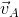
$\Delta \vec{v}$ = $\vec{v_{B}}$ – $\vec{v_{A}}$

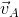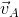Consider ΔAOB, angle between OA and OB is same as angle between $\vec{v_{A}}$ and $\vec{v_{B}}$ because $\vec{v_{A}}$ is perpendicular to vector OA and $\vec{v_{B}}$ is also perpendicular to vector OB.

OB = OA = r and

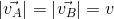
$\left | \vec{v_{A}} \right | = \left | \vec{v_{B}} \right | = v$

Component of Velocity of the Particle in Circular Path

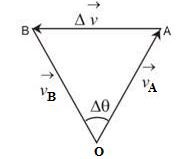
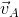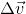
So, ΔAOB is similar to the triangle formed by $\vec{v_{A}}$ , $\vec{v_{B}}$ and $\Delta \vec{v}$

Thus,From geometry we have, Δv/v = AB/r

Now AB is approximately equal to vΔt.

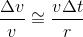
$\frac{\Delta v}{v}\cong \frac{v\Delta t}{r}$

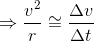
$\Rightarrow \frac{v^{2}}{r}\cong \frac{\Delta v}{\Delta t}$

In the limit Δt → 0 the above relation becomes exact, we have

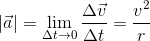
$\left | \vec{a} \right |=\lim_{\Delta t\to0 }\frac{\Delta \vec{v}}{\Delta t}=\frac{v^{2}}{r}$

This is the magnitude of the acceleration. The direction 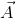$\vec{a}$ is instantaneously along a radius inward towards the centre of the circle, because of this 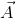$\vec{a}$ is called radial or centripetal acceleration. The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.

Refer this video for better understanding about circular motion:-

Problem 3:

The moon revolved about the earth making a complete revolution in 2.36 mega second. Assume that the orbit is circular and has a radius of 385 mega meter. What is the magnitude of the acceleration of the moon towards the earth?

Solution:-

Here first of all we calculate speed v of the moon which is given by v = 2πR/T

where R = 385 mega meter = 385 × 10⁶ m

and T = 2.36 mega second = 2.36 × 10⁶ sec.

Hence v = 1020 m/sec.

The magnitude of centripetal acceleration is

a = v²/R = 0.00273 m/sec².

From the above observation we conclude that, the magnitude of the acceleration of the moon towards the earth would be 0.00273 m/sec².

In the previous enquiry we have discussed the uniform circular motion in which the particle has constant speed. If the particle's speed varies with time then the motion will be no more uniform but a non-uniform circular motion. Let us discuss about this motion using the concept of vectors.

Simulation for Car and Curves

This animation is used to explain why a passenger slides to the "outside" of a curve while riding inside a car is NOT an example of centrifugal forces. Instead is is a combination of centripetal force and inertia. It emphasize that when an object moves to the outside of a circle it is because of a lack of enough centripetal force and inertia keeps it moving in a straight line.

Non uniform circular motion:-

Non Uniform Circular Motion

Let us use the vector method to discuss non-uniform circular motion.

In the side figure, $\hat{e_{r}}$ and $\hat{e_{\theta }}$ are unit vectors along radius and tangent vector respectively. In terms of er and eθ the motion of a particle moving counter clockwise in a circle about the origin in figure 2.30 can be described be the vector equation.

$\vec{v}=\hat{e_{\theta }v}$

In this case, not only $\hat{e_{\theta }}$ but v also varies with time. We can obtain instantaneous acceleration as,

$\vec{a}=\frac{d\vec{v}}{dt} =\hat{e_{\theta }}\frac{d\theta }{dt}+v(\frac{d\hat{e_{\theta }}}{dt})$

a-vector =(d v-vector )/dt = e-unit-vector θ dθ/dt + v(dθ)/dt

Again,

$\frac{d\hat{e_{\theta }}}{dt}=\frac{\hat{e_{r}}v^{2}}{r}$

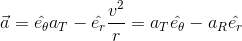
$\vec{a}= \hat{e_{\theta }}a_{T}-\hat{e_{r}}\frac{v^{2}}{r}=a_{T}\hat{e_{\theta }}-a_{R}\hat{e_{r}}$

Here, a_T = dv/dt and a_R = v²/r

The first term, $\hat{e_{\theta }}a_{T}$ is the vector component of $\vec{a}$ that is tangential to the path of the particle and arises from a change in the magnitude of the velocity in circular motion, called tangential acceleration whereas a_R centripetal acceleration.

The magnitude of $\vec{a}$ is

$\left | \vec{a} \right | = \sqrt{({a_{T}}^{2}+{a_{N}}^{2})}$

Problem 4:

Point A travels along an arc of a circle of radius r as shown in figure given below. Its velocity depends on the arc coordinates l as v = A √l where A is a constant. Let us calculate the angle α between the vectors of the total acceleration and of the velocity of the point as a function of the coordinate l.

Solution:-

It is seen from figure shown above that the angle α can be found by means of the

formula tan α = a_R/a_T. Let us find a_R and a_T.

a_R = v²/r=(A² l)/r; a_T= dv/dt = dv/dl = A/(2√l)×A√l = A²/2

Hence tan α = 2l/r.

Problem 5 (JEE Main):

Position vector of a particle moving in x-y palne at time t is

$\vec{r} = a\left ( 1-cos\omega t \right )\hat{i}+asin\omega t\hat{j}$ .

What will be the path of the particle?

Solution:-

x = a (1-cos ωt)

y = a sinωt

From first equation, we get

acos ωt = a-X …... (1)

From second equations, we get,

a sin ωt = y

Squaring and adding Eqs. (1) and (2), we get,

(X-a)² + y² = a²

This is an equation of a circle of radius a and ceter at (a,0).

Centripetal and centrifugal forces are equal in magnitude and opposite in direction.
Centripetal and centrifugal forces cannot be termed as action and reaction since action and reaction never act on same body.
Basic requirement for a body to complete motion in a vertical circle, under limiting conditions, is that the tension in the string must not vanish before it reaches the highest point. If it vanishes earlier, it will be devoid of the necessary centripetal force required to keep the body moving in a circle.
Cetrifugal force is the fictitious force which acts on a body, rotating with uniform velocity in a circle, along the radius away from the centre.

Question 1:-

When a body is moving in circular motion in a circular orbit at constant speed, it is in

(a) equilibrium (b) not in equilibrium

Question 2:-

A body executes uniform circular motion

(a) its velocity is constant (b) its acceleration is constant

Question 3:-

In case of rigid body, the only possible type of internal motion is:

(a) linear (b) circular

Question 4:-

When a body moves with a constant speed along a circle:

(a) its velocity remains constant (b) no force acts on it

Question 5:-

To move a body in a circle, which of the following forces is needed:

(a) centrifugal (b) gravitational

Q.1	Q.2	Q.3	Q.4	Q.5
a	c	b	c	c

Related Resources

You might like to refer Banking of Roads.
For getting an idea of the type of questions asked, refer the Previous Year Question Papers.
Click here to refer the most Useful Books of Physics.
To get answer to any question related to circular motion click here.

To read more, Buy study materials of Kinematics comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here.