Scalars and Vectors
Table of Content |
Different physical quantities can be classified into the following two categories:

Scalars
 Scalar quantities are those quantities which require only the magnitude for their complete specifications. Physical quantities which can be completely specified by a number and unit, and therefore have the magnitude only, are scalars. Some physical quantities which are scalar are mass, length, time, energy, volume, density, temperature, electric charge, electric potential etc. These examples obey the algebraic law of addition.
Scalar quantities are those quantities which require only the magnitude for their complete specifications. Physical quantities which can be completely specified by a number and unit, and therefore have the magnitude only, are scalars. Some physical quantities which are scalar are mass, length, time, energy, volume, density, temperature, electric charge, electric potential etc. These examples obey the algebraic law of addition.
Vectors

Vector quantities are those quantities which require magnitude as well as direction for their complete specifications. Vectors are physical quantities, which besides having both magnitude and direction also obey the law of geometrical addition. (The law of geometrical addition, i.e. the law of triangular addition and law of parallelogram are discussed later in this chapter). Some physical quantities, which are vectors are displacement, velocity, acceleration, force, electric intensity, magnetic intensity, magnetic moment etc. Vector quantities cannot, in general, be added in algebraically.
Important Note:- Electric current possesses magnitude and direction (through the conductor), but it is not a vector quantity. Electric current is a scalar quantity.
Representation of a Vector:-
Since vectors have directions, any representation of them has to include the direction.
 To represent a vector we use a line with an arrow head. The length of the line represents the magnitude of vector and direction of the arrow represents the direction of the vector. Let us start with a vector quantity called displacement. In the enclosed figure the change of position from point O to A is represented graphically by the directed line segment with an arrowhead to represent direction of motion.
To represent a vector we use a line with an arrow head. The length of the line represents the magnitude of vector and direction of the arrow represents the direction of the vector. Let us start with a vector quantity called displacement. In the enclosed figure the change of position from point O to A is represented graphically by the directed line segment with an arrowhead to represent direction of motion.
Vector is a Physical quantity and all physical quantities have units. Hence, the vectors also have units, they are called unit vectors.
A vector can be represented by observing the following steps:
(a) Draw a line parallel to the direction of vector.
(b) Cut a length of the line so that it represents the magnitude of the vector on a certain convenient scale.
(c) Put an arrowhead in the direction of the vector.
(d) A vector is written with an arrowhead over its symbol like “ ”.
”.
Unit Vectors
A unit vector is a vector having a magnitude of unity. Its only purpose is to describe a direction in space. On x-y co-ordinate system  denote unit vector in positive x direction and
denote unit vector in positive x direction and  denotes unit vector in positive y direction.
denotes unit vector in positive y direction.
Any vector in x – y plane can be represented in terms of these unit vectors  and
and  .
.
Similarly any vector in a 3 dimensional x y z space can be represented in terms of unit vectors  ,
,  and
and  . Here,
. Here,  is the unit vector in the positive z direction, as shown in figure above.
is the unit vector in the positive z direction, as shown in figure above.
Collinear vectors:- Vectors having a common line of action are called collinear vectors. There are two types of collinear vectors. One is parallel vector and another is anti parallel vector.
.jpg)
Parallel Vectors:- Two or more vectors (which may have different magnitudes) are said to be parallel (θ = 0°) when they are parallel to the same line. In the figure below, the vectors 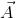 and
and 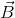 are parallel.
are parallel.
Anti Parallel Vectors

Two or more vectors (which may have different magnitudes) acting along opposite direction are called anti-parallel vectors.In the figure below, the vectors 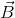 and
and  are anti parallel vectors.
are anti parallel vectors.
Equal Vectors:- Two or more, vectors are equal if they have the same magnitude (length) and direction, whatever their initial points. In the figure above, the vectors A and B are equal.
Negative Vectors:- Two vectors which have same magnitude (length) but their direction is opposite to each, other called the negative vectors of each other. In figure above vectors A and C or B and C are negative vectors.
Null Vectors:- A vector having zero magnitude an arbitrary direction is called zero vector or ‘null vector’and is written as = O vector. The initial point and the end point of such a vector coincide so that its direction is indeterminate. The concept of null vector is hypothetical but we introduce it only to explain some mathematical results.
Properties of a Null Vector
(a) It has zero magnitude.
(b) It has arbitrary direction
(c) It is represented by a point.
(d) When a null vector is added or subtracted from a given vector the resultant vector is same as the given vector.
(e) Dot product of a null vector with any vector is always zero.
(f) Cross product of a null vector with any vector is also a null vector.
Invariance of the Vector:- Any vector is invariant so it can be taken anywhere in the space keeping its magnitude and direction same. In other words, the vectors remain invariant under translation.
Co-planar Vector:- Vectors situated in one plane, irrespective of their directions, are known as co-planar vectors.
Localized Vectors:- Vector whose initial point (tail) is fixed is said to be a localized or a fixed vector.
Non-localized Vectors:- Vector whose initial point (tail) is not fixed is said to be a non-localized or a free vector.
Refer this video for better understanding about scalar and vector:-
Question 1:-
A ship sets out to sail a point 124 km due north. An unexpected storm blows the ship to a point 72.6 km to the north and 31.4 km to the east of its starting point. How far, and in what direction, must it now sail to reach its original destination?
Solution:-
Assumption:-

We assume that the ship was initially at point O from where it was drawn to the new position A and finally it went to its destination to reach point D(shown in the figure below).
We assume that the position vector of point D relative to point A is given by vector 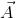 such that the vertical and horizontal components of the vector describe the motion of the ship lately.
such that the vertical and horizontal components of the vector describe the motion of the ship lately.
We also assume that the position vector of point D relative to point O is given by vector whereas the position vector of point A relative to point O is given by vector 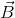 .
.
For vector  (refer diagram above, the red color vector),
(refer diagram above, the red color vector),
Since this is a position vector for point D relative to O, it has only vertical vector component, given as:

We have shown the vertical component of vector  in the figure above in red color to avoid confusion.
in the figure above in red color to avoid confusion.
The horizontal vector component of this vector is zero and can be written as:

For vector 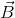 (refer diagram above, the blue color vectors),
(refer diagram above, the blue color vectors),
Since the ship was driven 31.4 km east and 72.6 km north, the horizontal and vertical vector component of vector 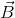 is given as:
is given as:


For vector  (refer diagram above, the black color vectors),
(refer diagram above, the black color vectors),
Since the ship was meant to go only in the north, the horizontal displacement of the ship, when it is at point A, from its destination is 31.4 east. Therefore the horizontal vector component of vector 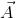 can be written as:
can be written as:

The negative sign shows that the vertical vector components points in the west that is opposite to the direction of the unit vector  .
.
The vertical vector component of vector 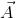 can be calculated from the difference between vertical vector component of vector
can be calculated from the difference between vertical vector component of vector  and the vertical vector component of vector
and the vertical vector component of vector 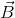 as:
as:


Now, we have the components of vector 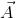 , we can calculate the direction in which the ship must move and by what distance.
, we can calculate the direction in which the ship must move and by what distance.
Let us assume that the angle subtended by vector 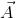 on negative x axis is ?. The sign of the angle will indicate if the angle was measured clockwise or counterclockwise.
on negative x axis is ?. The sign of the angle will indicate if the angle was measured clockwise or counterclockwise.
The angle can be calculated as:
? = tan-1 (ay/ax)
Also from the components of vector 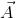 , we have that
, we have that
ay = 51.4 km
ax = -31.4 km
Substituting the values in the equation above, we have
? = tan-1 (51.4 km/-31.4 km)
= - 58.5°
The negative sign indicates that the angle is measured in the counterclockwise direction.
Therefore the ship must go in the direction 58.5° north of west to reach its destination.
The distance that the ship needs to travel, to reach its destination is equal to the magnitude of vector 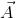 . We can write the vector in the unit vector notation as:
. We can write the vector in the unit vector notation as:


The magnitude of this vector is:
|a| = √(ax)2 +(ay)2
= √(-31.4 km)2 +(51.4 km)2
= 60.2 km
Therefore the ship has to go 60.2 km in the direction of vector 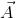 .
.
Related Resources
-
Click here for the Detailed Syllabus of IIT JEE Physics.
-
Look into the Sample Papers of Previous Years to get a hint of the kinds of questions asked in the exam.
-
You can get the knowledge of Useful Books of Physics..
To read more, Buy study materials of Units & Dimensions comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here
View courses by askIITians


Design classes One-on-One in your own way with Top IITians/Medical Professionals
Click Here Know More

Complete Self Study Package designed by Industry Leading Experts
Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child
Click Here Know More

