Trigonometric Inequality | IIT JEE Inequality Formulas

 

Trigonometric inequality is a vital topic in the IIT JEE Mathematics syllabus. Trigonometry inequality contains one or many trigonometry functions of the function x in the form of R [f(x), g(x)...] > 0 (or < 0), in which f(x), g(x),... are trigonometric functions of x. Solving for x implies searching for the values of x which make the inequality true. All such values of x constitute the solution set of the given trigonometric inequality. Some examples of trigonometric inequalities are

sin x + sin 2x > -sin 3x

sin x + sin 3x < 1

2tan x + tan 2x > 3cot x

cos 2x -2 > -3sin x

IIT JEE trigonometric inequality questions are an amalgamation of both average as well as hard questions. We list here some of the illustrations to give an idea about the type of questions asked from this topic.

Illustration:

Find the solution set of inequality sinx > 1/2.

Solution:

When sinx = ½, the two values of x between 0 and 2π are π/6 and 5π/6.

y = sin x

From, the graph of y = sinx, it is obvious that, between 0 and 2π

sinx > 1/2 for π/6 < x < 5π/6.

Hence sinx 1/2 ⇒ 2nπ + π/6 < x < 2nπ + 5π/6.

The required solution set is ∪ (2nπ +π/6, 2nπ +5π/6).

Illustration:

Find the solution set of inequality cosx > –1/2.

Solution:

Form the graph of y = cosx, it is obvious that cosx > –1/2

If -2π/3≤x≤2π/3.

 

y = cos x

Hence general value for cosx > -1/2

⇒ 2nπ -2π/3 ≤ x ≤2nπ + 2π/3.

The required solution set is ∪ (2nπ -2π/3,2nπ +2π/3).

Illustration:

Solve:

sin4x = 1 + tan8x.

Solution: Considering the both sides one by one

L.H.S. = sin4x < 1.

R.H.S. = 1 + tan8x > 1.

L.H.S. = R.H.S. only when

sin4x = 1 and 1 + tan8x = 1 ⇒ sin2x = 1 and tan8x = 0.

which is never possible, since sinx and tanx vanish simultaneously.

Therefore, the given equation has no solution.

Illustration:

Solve sin2x + cos2y = 2sec2z.

Solution:

 L.H.S. = sin2x + cos2y < 2.

 R.H.S. = 2 sec2z > 2.

 Hence L.H.S. = R.H.S. only when

  sin2x = 1, cos2y = 1, sec2z = 1

   ⇒ |sin x| = 1, |cos y| = 1, |cos z| = 1

   ⇒ x = (2m+1) π/2, y = nπ and z = tπ where m, n, t are integers.

Illustration:

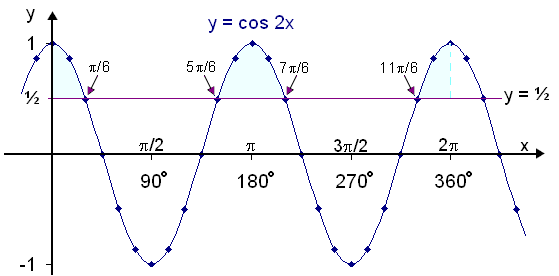
Solve the inequality cos 2x ½ on the interval 0 < x < 2 .

Solution:

First solve the equation cos 2x = ½.

2x = cos−1(½) = 60° /180° =/3 + k·2 x = /6 + k·

If we choose k = 0 and 1 we get the solutions /6 and 7/6 (30° and 210°).

We try to find out these values by using the rule

 cos x = cos (−x)

2x = −/3 + k·2

x = −/6 + k·

If we use the values k = 1 and 2 we get the solutions 5/6 and 11/6 (150° og 330°).

Now we draw a diagram so that we can see the solutions to the inequality

 

The diagram shows the graphs of y = cos 2x and y = ½. The shaded intervals above the horizontal line show the solutions to the inequality. The solutions are therefore the following intervals:

0 x /6  or  5/6 x 7/6  or 11/6 x < 2

To have a clear idea about the trigonometry inequality questions, please look into the sample papers.

Watch this Video for more reference
 

To read more, Buy study materials of Trigonometry comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.