Trigonometric Functions of Sum and Difference of Two Angles | JEE Trigonometry Sum and Difference of Angles
Table of Content |
Is sin (A + B) = sin A + sin B?
At the initial learning about trigonometric, every student has the basic doubt whether sin(A + B) is equals to sin A + sin B or not same as x(2 + 3) = 2x + 3x.
So let’s clear this doubt here by taking an example.
sin90° = sin(60° + 30°) = sin60° + sin30°
LHS: Sin90° = 1
Clearly, we can see that LHS ≠ RHS and thus sin (A + B) is not equals to sin A + sin B in general. Then let us find its actual simplification in the next section.
How to derive sin (A + B) formula?
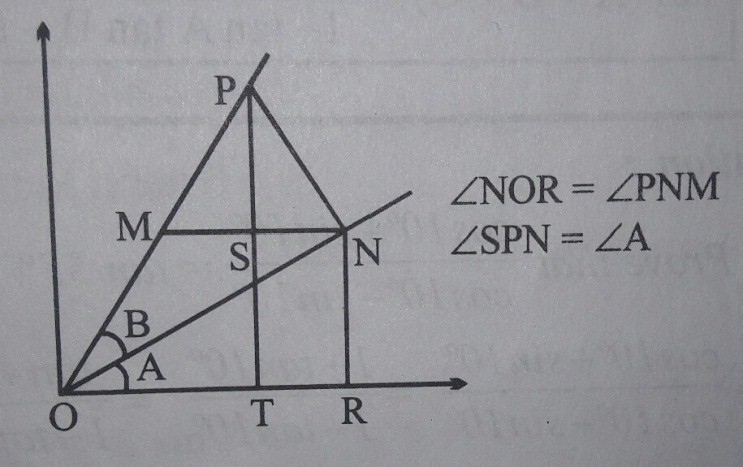
For deriving sin (A + B) formula, let us now assume that A + B ≤ 90° thus we shall take two points P and N on the Cartesian plane such that ON makes an angle of A with the x – axis and OP makes an angle of (A + B). See the figure to understand the derivation below.
= cosA sinB + sinA cosB
Thus we can now say that sin (A + B) = sinA cosB + cosA sinB. ……. (1)
From here, we can also derive the other compound angles formula.
For sin(A – B), if we just replace B with –B in equation (1). We get
sin (A - B) = sinA cos(-B) + cosA sin(-B)
Thus on further simplification, we get
sin (A - B) = sinA cosB - cosA sinB ……………….(2)
For cos(A + B), if we replace A by π/2 + A in equation (1),
On simplification,
cos(A + B) = cosA cos B + sinA sinB ……… (3)
And for cos (A – B), if we just replace B with –B in equation (3). We get
cos(A - B) = cosA cos(-B) + sinA sin(-B)
cos(A - B) = cosA cosB - sinA sinB ………… (4)
Although, we have assumed at the beginning that A + B ≤ 90°, but still the above formulas are valid for other condition too.
What are compound angles formulas?
Compound angles formulas are the formulas in trigonometry involving sum or difference of two or more angles. We have also discussed and 
derived the compound angle formulas for sine and cosine. We will list all these and some addition formulas below:
-
sin(A + B) = sinA cosB + cosA sinB
-
sin(A - B) = sinA cosB - cosA sinB
-
cos(A + B) = cosA cos B - sinA sinB
-
cos(A - B) = cosA cosB + sinA sinB
Few other formulas:
Important Note: If we assume A = 45o and B = A in above formulas,
How can we transform the product into sum or difference formulae?
We need the help of compound angles derived above to get the relation between the product and sum or difference formulae.
Since we know that:
-
sin(A + B) = sinA cosB + cosA sinB
-
sin(A - B) = sinA cosB - cosA sinB
-
cos(A + B) = cosA cos B + sinA sinB
-
cos(A - B) = cosA cosB - sinA sinB
Now, to calculate product formula for - 2sinA cosB, if we add sin (A + B) and sin (A – B) from the above formulas, we can easily get
2sinA cosB = sin (A + B) + sin (A – B) …………………………. (5)
Similarly using the above four formulas we can get other relations as well,
2cosA sinB = sin (A + B) - sin (A + B) …………………………… (6)
2cosA cosB = cos (A + B) + cos (A – B) ………………………… (7)
2sinA sinB = cos (A - B) - cos (A + B) …………………………… (8)
With this derived product formulas, we can now easily convert the product of two trigonometric ratio of different or same angle into sum or difference of the ratios.
How can we transform the sum or difference into product formulas?
For the conversion, from sum or difference into product formulae, let us assume:
A + B = C and A – B = D, which gives
Using these assumptions in equations 5, 6, 7 and 8. and simplification, we get
All these above formulae are very important in trigonometry.
Give some important identities related to compound angles
Below are few important identities, which is used to simplify the complex trigonometric equations.
Note:- All these above identities can be easily derived by using compound angles formulae.
Highlight Trigonometric Ratios of multiple and submultiple angles
So first question here may be that what do we mean by multiple and submultiple angle. So to understand it, multiple angles here mean if we have an angle A, then all the angles which are integer multiple of A, that is, nA, will be considered as the multiple angles of A. While all the angles of the form A/n, will be called as the Submultiple Angles. Here, n is any integer.
So,
sin2A = sin(A + A) = sinA cosA + cosA sinA
(using the formula for sin(A + B))
= 2 sinA cosA
Thus, sin2A = 2sinAcosA
Similarly, cos2A = cos(A + A) = cosA cosA – sinA sinA
(using the formula for cos(A + B))
= cos2A – sin2A
= 2cos2A – 1 = 1 – 2 sin2A
Or we may write,
Similarly, we may also derive it for other trigonometric ratios. Here we are presenting all the other important formulas for multiple and submultiple angles.
Formulae in terms of tan2A:
What are the applications for compound angle formulae?
We have wide application of compound angle formulae in trigonometry. Let’s have few examples to understand the same.
Finding values of 15° and 75°
To find the value of sin 15° or sin 75°
Since we can write 15° = 45° - 30° and 75° = 45° + 30°
Thus,
(using the formula of sin (A – B), and writing the values of basic trigonometric ratios)
(Using the formula of sin (A + B), and writing the values of basic trigonometric ratios)
Now let’s find the values of tan 15° and tan75°
Again using the same concept but different formulas, we can write:
Here we have used the formula of tan (A - B) and tan(A + B).
Finding values of 18°
Let θ stands for 18°, so that 2θ = 36° and 3θ = 54°.
Hence, 2θ = 90° - 3θ
and therefore
sin2θ = sin (90° – 3θ) = cos3θ
∴ 2 sinθ cosθ = 4 cos3θ – 3cosθ
Hence, either cosθ = 0, which gives θ = 90°, or
2 sinθ = 4cos2θ – 3 = 1 – 4sin2θ
∴ 4 sin2θ + 2 sinθ = 1
By solving this quadratic equation, we have
(In our case sinθ is necessarily a positive quantity. Hence we take the upper sign)
The remaining trigonometric ratio of 18° may be now found.
Since 72° is the complement of 18°, the value of the ratios for 72° may be obtained.
To find the trigonometric functions of an angle of 36°
Since cos2θ = 1 - 2 sin2θ,
The remaining trigonometric functions of 36° may now be found.
Also, 54° may be found.
More Readings