JEE Important Trigonometric Functions

 

Table of Content

What is Trigonometry? Define the six Trigonometric functions How do you find the six Trigonometric Functions of an angle? Trigonometric Function (or ratio) for 45° angle Trigonometric Function for 30° & 60° angle Trigonometric Functions (or ratios) for 0° and 90° Which trignometry functions are even or odd? What are sine and cosine? Why is the cosine function even? How to find the trigonometric functions of an angle of 18°?

 

What is Trigonometry?

The word trigonometry is derived from the three greek words

In the ancient sense trigonometry defines relation between elements of a triangle. In a triangle there are six basic elements, three sides and three angles. Any three lines segments will form a triangle iff they satisfy three triangular inequalities i.e. the sum of any two lines segment is greater than third side. In Euclidean geometry the sum of three angles of a triangle is 180°. These requirements impose limitations on the manner in which the relations between the elements are defined.

Define the six Trigonometric functions

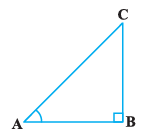
In trigonometry, we need to evaluate six basic trigonometric functions. They are named as - sine, cosine, tangent, cosecant, secant, and cotangent – for a single angle in a right angled triangle. They are also called as – Sin, Cos, Tan, Cosec, Sec and Cot respectively in short.

In a right angled triangle, we have base (or adjacent) (B), perpendicular (or opposite) (P) and hypotenuse (H). So on the basis of these sides, trigonometric functions are defined as follows:

Note: - sec, cosec and cot functions are reciprocal of cos, sin and tan respectively. For Example - if sin θ = 1/2 than cosece θ = 2, similarly for cos & sec and tan & cot functions.

How do you find the six Trigonometric Functions of an angle?

In Basic trigonometry few angles like 0°,3°, 45°^, 60° & 90° are considered as very basic angles. So we first here will try to learn finding the values of trigonometric functions for these angles. Between 0° and 90°  is considered as the first quadrant. So these means here, we are only considering the first quadrant only.
 

Trigonometric Function (or ratio) for 45° angle

Consider a right angled triangle ABC right angled at B (shown in figure). Angle BAC is θ. Assuming θ = 45°^, than angle ACB will also be equals to 45°. Thus, AB = BC. So by using phythagorus theorem, we can easily find that, AB : BC : AC = 1 : 1: √2.

Now, let’s take the situation where the angle A tends to become right angle.

See the below figure to understand the situation graphically. If, ∠A  tends to approach 90°, Side AC (Hypotenuse) will become equals to BC (perpendicular) and side AB (base) will become zero.

Thus we can tabulate all these values for different angles of trigonometric functions.

*Note: In the above table n.d. represents not defined or infinity.
 

Which Trigonometry functions are even or odd?

Functions are called as even functions iff

f(-x) = f(x)

Graphically, the functions are even iff they are symmetric about the y – axis.

In Trigonometry, cos (-x) = cos (x), sec (-x) = sec (x). And Thus cosine and secant functions are even functions. We may also look their graph to understand the same.

Functions are called as odd functions iff

f(-x) = – f(x)

Graphically, the functions are even iff they are odd symmetric about the y – axis.

In Trigonometry, sin (-x) = -sin (x), tan (-x) = -tan (x), cosec (x) = -cosec (x), cot (-x) = -cot (x) And Thus sine, tangent, cosecant and cotangent functions are odd functions. We may also look their graph to understand the same.
 

 

What are sine and cosine?

Sine function, in trigonometry, is defined for a right angled triangle for any acute angle α.

Mathematically, sine of any angle α is the ratio of length of perpendicular (or opposite) side to the length of hypotenuse. 

Since the angle α can be any value between o to 360. And in general 0 + 2nπ ≤  α < 360 + 2nπ, where, n can be any integer value. And thus the value of sine repeats after every fixed interval of 2π.

In Trigonometry, cosine and secant functions are even functions. 

Basic Trigonometric Identities:

• sin²⁡θ + cos²⁡θ =1; where θ ∈R

• 1+ tan²⁡θ = sec²⁡θ or sec²⁡θ – tan²⁡θ =1

• 1+cot²⁡θ = cosec²⁡θ or cosec²⁡θ – cot²⁡θ =1

• sin⁴⁡θ + cos⁴θ = 1 - 2 sin²⁡θ cos²⁡θ

• sin⁶⁡θ + cos⁶⁡θ  =1 - 3 sin²⁡θ cos²⁡θ

Note:

• (sec⁡θ – tan⁡θ) is reciprocal of (sec⁡θ + tan⁡θ) and vice versa

• (cosec⁡θ – cot⁡θ) is reciprocal of (cosec⁡θ + cot⁡θ) and vice versa

Using above identities thousands of other identities can be proved. While proving identities you can use rationalization, factorization and many other similar mathematical operations.
 

How to find the trigonometric functions of an angle of 18°

Let θ stands for 18°, so that 2θ = 36° & 3θ = 54°.

Hence, 2θ = 90° - 3θ

and therefore

sin⁡ 2θ =sin⁡ (90°- 3θ ) =cos⁡3θ

∴ 2sinθ cos⁡θ = 4 cos²⁡θ – 3cosθ

Hence, either cosθ = 0, which gives θ = 90°, or

2 sin⁡ θ = 4 cos²⁡θ – 3 =1 – 4 sin²θ 

∴ 4 sin²⁡θ + 2sinθ =1

By solving this quadratic equation, we have

(In our case sin θ is necessarily a positive quantity. Hence we take the upper sign)

The remaining trigonometric ratio of 18° may be now found.

Since 72° is the complement of 18°, the value of the ratios for 72° may be obtained.

To find the trigonometric functions of an angle of 36°

Since cos⁡2θ =1 – 2 sin²⁡θ,

The remaining trigonometric functions of 36° may now be found.

Also, 54° may be found.
 

For more conceptual clarity on periodicity and graphical representation please refer the video

Illustration 1:

Find all trigonometric functions of an angle  in the third quadrant for which 
Solution: Before proceeding towards the solution, draw the figure so as to have a clear picture of the question. 


As in the Figure, cosθ= x/R = -5/6 and also we may consider x = -5 and R = 6.
Since, x² + y² = 6² = R² = 36 we find that y = -√R² - x² = -√11

Note that the negative signs indicate the third quadrant. And hence all the rest ratios follow

Illustration 2: Evaluate the value of the expression

3[sin⁴(3π/2 - α) + sin⁴(3π + α)] – 2 [sin⁶(π/2 + α) + sin⁶(5π - α)].

Solution: The given expression is

3[sin⁴(3π/2 - α) + sin⁴(3π + α)] – 2 [sin⁶(π/2 + α) + sin⁶(5π - α)].

= 3[(cos⁴α + sin⁴ α) – 2(cos⁶α + sin⁶ α)]

= 3 [(1-2sin²α cos²α) -2(1-3sin²α cos²α)] = 1.

Illustration 3: Find the value of

3(sin x – cos x)⁴ + 6(sin x + cos x)² + 4(sin⁶x + cos⁶x).

Solution: The given expression is

3(sin x – cos x)⁴ + 6(sin x + cos x)² + 4(sin⁶x + cos⁶x)

= 3 (1 - sin 2x)² + 6(1 + sin 2x) + 4[(sin²x + cos²x)³ -3sin²x cos²x (sin²x + cos²x)]

= 3 (1 - 2sin2x + sin²2x) + (6 + 6 sin2x) + 4(1-3sin²x cos²x)

= 3 (1- 2sin2x + sin²2x + 2 + 2sin2x) + 4 [1- ¾ sin²2x]

= 13 + 3 sin²2x – 3 sin²2x = 13.

Illustration 4: If cos (a + b) = 4/5, sin (a-b) = 5/13 and a and b lie between 0 to π/4, find tan 2a.

Solution: It is given that cos (a + b) = 4/5, sin (a-b) = 5/13

It follows that sin (a + b) = 3/5, cos (a-b) = 12/13

Hence, tan (a+b) = 3/4 and tan (a-b) = 5/12

Hence, this implies tan [(a+b) + a-b] =

[tan (a+b) + tan (a-b)]/ [1 + tan(a+b)tan(a-b)]

= (3/4 + 5/12)/ (1 – 3/4. 5/12)

Hence, tan 2a = 14/12. 48/33 = 56/33.

To read more, Buy study materials of Trigonometry comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.
 

More Readings

Trigonometric Functions