Inverse Circular Function (Inverse Trigonometric Functions)
Inverse of trigonometric ratios exists.
We know that y = sin x means y is the value of sine of angle x if we consider domain and co-domain both as set R of a real numbers. Sine ratio as seen from the fig. is many-one into function.
But it is clear that if we restrict the domain to [-π/2,π/2] and range to
[–1, 1], then. Y = sin x is one-one onto and hence it is invertible.
So, y = sin x x ∈ [-π/2,π/2], y ∈ [–1, 1]
⇒ x = sin–1 y y ∈ [–1, 1]. x ∈ [-π/2,π/2]
This value of x is called the principle value, i.e. belonging to [-π/2,π/2] and [-π/2,π/2] range and it is called principal value range.
Note: The smallest numerical angle is called principal value.
In general the inverse circular functions with their domain and range can be tabulated as:
Note: Principal value range of all Inverse Circular function is very important as the function is defined only in this range.
Pause: Odd function are defined as f(–x) = –f(x) and even function as f(–x) = f(x).
The inverse circular functions are defined as below:-
1. sin–1 (–x) = –sin–1 x, –1 < x < 1 Odd function
2. cos–1 (–x) = π –cos–1 x, –1 < x < 1 Neither odd nor even
3. tan–11 (–x) = –tan–1 x, x ∈ R Odd function
4. cot–1 (–x) = π – cot–1 x, x ∈ R Neither odd nor even
5. cosec–1 (–x) = –cosec–1 x, x < –1 or x > 1 Odd function
6. sec–1 (–x) = π –sec–1 x, x < –1 or x > 1 Neither odd nor even
Let us see the proof of any one of the above.
Proof 2:
Let cos-1 (–x) = θ, then cos θ = –x
or, – cos θ = x or cos (π – θ) = x
or, π – θ = cos-1 x or cos-1 (–x) = π –cos-1 x
Similarly we can prove other results.
Caution: Instead of taking cos (π – θ) equal to – cos θ, we could have taken cos (π + θ). We opt for cos (π – θ) because (π – θ) lies in a principal value range i.e. 0 ≤ cos-1 x ≤ π.
Illustration:
Find cot-1 (–1)
Solution:
cot-1 (–1) = π – cot-1 (1)
= π -π/4 [? cot-1 (–x) = π – cot-1 x]
= 3π/4.
Properties of Inverse Circular Function
1. Self adjusting Properties
(a) sin (sin-1 x) = x, x ∈ [–1, 1]
Let sin-1 x = θ, θ &isin (-π/2,π/2) ……… (1)
Then x = sin θ
From (1) putting the value of θ in (2), we get, ……… (2)
sin (sin-1 x) = sin (θ) = x
(b) sin-1 sin x = x, x ∈ [-π/2,π/2].
Let sin x = y, y ∈ [–1, 1] ……… (1)
Then x = sin-1 y ……… (2)
Putting the value of y in (2) from (1), we get,
sin-1 sin x = x
Illustration:
Evaluate sin-1 sin 5, 5 is radian
Solution:
We know sin-1 sin x = x, x ∈ [-π/2,π/2] or x ∈ [–1.57, 1.57]
We can write, 5 = 2 π + 5 – 2 π
sin 5 = sin (2 π + (5 – 2π))
= sin (5 – 2 π), 5 – 2 π ∈ [–1.57, 1.57]
∴ sin-1 sin 5 = sin-1 sin (5 – 2π)
= 5 – 2π
2. Reciprocal Property
sin-1 (1/x) = cosec-1 x, x ≤ –1, or x ≥ 1
let cosec-1 x = θ ⇒ cosec θ, θ ∈ [-π/2,π/2] – {0}
⇒ LHS = sin-1 (1/(cosec θ )) = θ
⇒ sin-1 (sin θ) = θ which is true for above domain of θ
= cosec-1 x = RHS.
Note: cot-1 (1/x) = tan-1 x holds only for x > 0. This is because of principal value range of Inverse function cot and tan are different.
When x < 0, the principal value range is π/2 < cot-1 (1/x) < π, whereas -π/2 < tan-1x< 0. Hence equality will never hold in this case.
cot-1 (-1/2) = tan-1 (–x)
π – cot-1 (1/2) = –tan-1 x
cot-1 (1/2) = π + tan-1 x
Hence cot-1 (1/2) = { tan-1 x, x>0
π+tan-1 x, x< 0
Relation between Inverse Trigonometric Functions
1. sin-1 x + cos-1 x = π/2 x ∈ [–1, 1]
Let sin-1 x = θ, θ ∈ [-π/2,π/2]
⇒ x = sin θ,
⇒ x = cos (π/2-θ ),(π/2-θ ) ∈ [0, π]
⇒ cos-1 x = π/2 – θ
⇒ cos-1 x + sin-1 x = π/2 x ∈ [–1, 1].
We can express any inverse circular function in terms of the other by drawing a right-angled triangle. Thus, if we have to explain tan-1 x in terms of the other, then take the perpendicular of the triangle as x and base as 1. Now, hypotenuse is √(1+x2 )
θ = tan-1 x = cot-1 1/x = sin-1 x/√(1+x2 )=cos-11/√(1+x2 )=cosec-1√(1+x2 )/x= sec-1√(1+x2 )
Illustration:
Prove that sin cot-1 tan cos-1 x = x.
Solution:
Note: In such problems we proceed with the last term of LHS.
Here, LHS = sin cot-1 tan cos-1 x
Let cos-1 x = θ, x = cos θ
∴ tan θ = √(1+x2 )/x
tan cos-1 x= √(1+x2 )/x
(1) Reduces to, sin cot-1 (√(1+x2 )/x) …… (2)
Again let cot-1 √(1+x2 )/x = φ
√(1+x2 )/x = cot φ
∴ sin φ = x
Hence, (2) becomes
sin cot-1 √(1+x2 )/x = x = R.H.S.
Illustration:
Find the value of cos (2 cos-1 x + sin-1 x) at x = 1/5, Where 0 ≤ cos-1 x ≤ π, –&pi/2 ≤ sin-1 x ≤ π/2
Solution:
cos (2 cos-1 x + sin-1 x) = cos (cos-1 x + (cos-1 x + sin-1 x))
= cos (cos-1 x+ π/2)
= –sin cos-1 x …… (1)
Let cos-1 x = θ
⇒ x = cos θ
sin θ = √(1-x2 )
cos-1 x = θ – sin-1 √(1-x2 )
Now, (1) becomes
(2 cos-1 x + sin-1 x) = –sin cos-1 x = –sin-1 √(1-x2 )
= –√(1-x2 ) as –1 ≤ √(1-x2 ) ≤ 1
= – √(1-1/25) at x = 1/5
= – 2/5 √6.
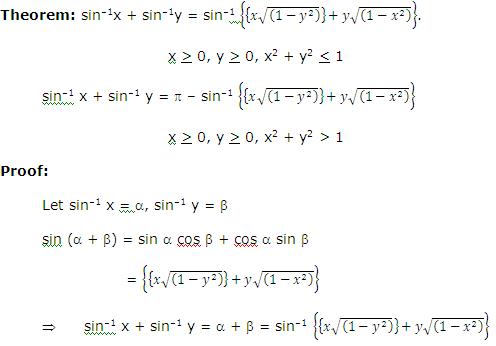
Since x ≥ 0, y ≥ 0 so RHS ∈ (0, π/2) but if x and y are such that
LHS > π/2 then above equation is not valid. So above equation is valid only when
sin-1 x + sin-1 y ≤ π/2
⇒ sin-1 x ≤ π/2 – sin-1 y
⇒ sin-1 x ≤ cos–1 y
taking sine ( ) both sides
sin (sin-1 x) < sin (cos–1 y)
(∴sine is an increasing function in [-π/2,π/2] )
⇒ x < √(1-y2 )
⇒ x2 + y2 < 1
So above relation is valid only when x2 + y2 ≤ 1
Now, if x2 + y2 > 1 then
Let us assume LHS = θ and RHS = φ
Then sin θ = sin φ, which is true only when θ = φ or θ = π – φ
⇒ sin-1 x + sin-1 y = π – sin-1 (x√(1-y2 )+y√(1-x2 )).
Illustration:
If sin-1 x + (sin-1 y + sin-1 z) = π/2
Solution:
Find out x2 + y2 + z2 + 2xyz.
Let sin-1 x = A, sin-1 y = B and sin-1 z = C
⇒ A + B + C = π/2
A + B = π/2 – C.
Let’s operate cos on both sides.
Note: That we have chosen to operate cos because it becomes easier to solve.
cos (A + B0 = cos (π/2 – C)
cos A cos B – sin A sin B = sin C
√((1-x2 ) ) √((1-y2 ) )-xy=z
xy + z = √((1-x2 )(1-y2 ) )
Squaring both sides
x2 y2 + z2 + 2xyz = 1 + x2 y2 – x2 – y2
x2 + y2 + z2 = 2xyz = 1
Hence proved.
Theorem: tan-1 x + tan-1 y = tan-1 {(x + y)/(1 – xy)} if xy < 1
= π –tan-1 (x + y)/(xy – 1) if xy > 1
= π/2 if xy = 1.
Proof:
Let tan-1 x = α so that tan α = x
and tan-1 y = β so that tan β = y
Also let tan-1 ((x+y)/(1-xy)) = γ so that tan γ = (x+y)/(1-xy)
We have then to prove that
α + β = γ
Now tan (α + β) = (tanα +tanβ )/(1-tanα tanβ )=(x+y)/(1-xy) = tan γ
So, the relation is proved
tan-1 x + tan-1 y = tan-1 ((x+y)/(1-xy)) …… (1)
Case I:
When x ≥ 0, y ≥ 0 and xy < 1, (x+y)/(1-xy) is positive
∴ tan-1 [(x+y)/(1-xy)] will be positive angle
Case II: When x ≥ 0, y ≥ 0 and xy > 1, (x+y)/(1-xy) is negative
∴ tan-1 ((x+y)/(1-xy)) will be negative angle.
Hence we add π to make it positive
∴ tan-1 x + tan-1 y = π + tan-1 [(x+y)/(1-xy)].
Case III: When xy = 1, (x+y)/(1-xy) = ∞ then
∴ tan-1 x + tan-1 y = tan-1 ∞ = π/2
Illustration:
Show that the equation
tan–1 {((x+1))/((x-1) )} + tan–1 {((x-1))/x} = tan–1 (–7) has no solution.
⇒ (x–2)2 = 0 ⇒ x = 2
Putting x = 2 in the equation, the equation becomes
tan–1 3 + tan–1 1/2 = tan–1 (–7)
Since x y = 3 . 1/2 > 1
So, tan–1 x + tan–1 y = π + tan–1 ((x+y)/(1-xy))
tan–1 3 + tan–1 1/2 = 3 + tan–1 ((3+1/2)/(1-3/2))
= π + tan–1 (–7) ≠ tan–1 (–7) = R.H.S.
Hence given equation has no roots as x = 2 does not satisfy the given equation.
Illustration:
Solve the equation
tan-1 2x + tan-1 3x = nπ + π/4
Solution:
We know that
So we have the following cases.
Case I:
2x . 3x < 1 ⇒ x2 < 1/6 ⇒ -1/√6 < x < 1/√6
For this
⇒ L.H.S. = tan-1 {(2x+3x)/(1-6x^2 )} = nπ + π/4
Taking tan of both the sides
5x/(1-6x2 ) = tan (nπ + π/4) = 1
⇒ 6x2 + 5x – 1 = 0
⇒ 6x2 + 6x – x – 1 = 0
⇒ (x + 1) (6x – 1) = 0
⇒ x = 1/6 or x = –1
Since –1 ∉ (-1/√6,1/√6)
Hence x = 1/6 is a solution.
Case II:
2x . 3x > 1 ⇒ x ∈ (-∞ ,-1/√6) ∪ (1/√6,∞ )
For this we have
LHS = π – tan-1 (5x/(6x2-1)) = nπ + π/4
⇒ tan (π -tan-1 (5x/(6x2-1)) )=tan(nπ + π/4)
⇒ –tan (tan-1 (5x/(6x2-1)) )=1
= 5x = 1 – 6x2
⇒ 6x2+ 5x – 1 = 0
⇒ (x + 1) (x – 1/6) = 0
⇒ x = –1, x = 1/6, since 1/6 ∉ (-∞ ,-1/√6)∪(1/√6,∞ ).
Hence x = –1 is another solution.
⇒ x = –1, 1/6 are solutions of the given equation.
Theorem:
2 tan-1 x = sin-1 2x/(1+x2 ), where |x| < 1
= cos–1 (1-x2)/(1+x2 ), where x > 0
= tan-1 2x/(1-x2 ), where |x| < 1.
Proof:
Let tan-1 x = θ, then tan θ = x
sin 2 θ = (2 tan θ )/(1+tan2 θ )=2x/(1+x2 )
⇒ 2 θ = sin-1 (2x/(1+x2 ))
⇒ 2 tan-1 x = sin-1 (2x/(1+x2 ))
Both sides are balanced for |x| < 1.
Caution:
Restriction on x is |x|< 1. To verify it suppose the formulae holds good even for x > 1.
Then L.H.S. = 2 tan-1 x
= 2 tan-1 (a no. 1 > 1) [for x > 1]
> π/2 [? tan-1 (>1) > π/4], [for principal values]
R.H.S. = sin–1 2x/(1+x2 ) which lies between -π/2 and π/2 for all values of x, [for principal values]
Thus, we see that for x > 1,
L.H.S. > π/2, whereas R.H.S. ≤ π/2.
Hence two cannot be equal.
Both sides are balanced for |x| < 1.
Note:For |x| > 1
2 tan-1 x = π – sin–1 2x/(1+x2 )
= π – cos–1 (1-x2)/(1+x2 )
= π – tan-1 2x/(1-x2 )
Illustration:
Show that the function y = 2 tan-1 x + sin-1 2x/(1-x2 ) is a constant for x ≥ 1. Find the value of this constant.
Solution:
We know, sin-1 2x/(1+x2 ) = 2 tan-1 x if |x| < 1
Here given x ≥ 1. So if we convert in above condition then we can get solution.
x ≥ 1 can be written as 1/x < 1.
So, for 1/x < 1
sin-1 2x/(1+x2 ) = sin-1 (2/x)/(1/x2 +1) = sin-1 2(1/x)/((1/x)2+1) = 2 tan-1(1/x)
Now, y = 2 tan-1 x + 2 tan-1 (1/x)
= 2 [tan-1 x + cot–1 x]
= π = const.
Illustration:
Show that 2tan-1 1/2 + tan-1 1/7 = tan-1 31/17.
Solution:
We have 2tan-1 1/2 = tan-1 (2-1/2)/(1-1/4) = tan-1 4/3
⇒ 2tan-1 ((4/3+1/7)/(1-4/21)) = tan-1 31/17
Illustration:
Solve 2tan-1(cosx) = tan-1(2cosecx).
Solution:
= tan-1[2cot x cos ecx] = tan-1(2 cosec x) (given)
⇒ cotx = 1 ⇒ x = nπ + π/4.
Illustration:
Show that tan-1 (x/√(a2-x2 )) = sin-1 (x/a), a > 0.
Solution:
Let sin-1 x/a = θ, then x = a sin θ, -π/2 < θ < π/2 as (x ≠ a)
⇒ x/√(a2-x2 )=(a sin θ )/√(a2-a2 sin2 θ ) = tan θ ⇒ tan-1 (x/√(a2-x2 ))
= tan-1 (tanθ) = θ = sin-1(x/a).
To read more, Buy study materials of Trigonometry comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.