Magnetic Flux Density or Magnetic Induction

Magnetic Effect of Current 

In 1820, Danish Physicist, Hans Christian Oersted observed that current through a wire caused a deflection in a nearby magnetic needle. This indicates that magnetic field is associated with a current carrying conductor.

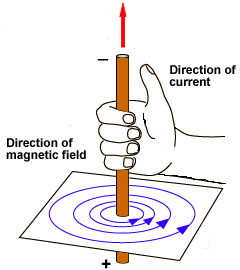
Maxwell’s Right Hand Cork Screw Rule

If a right handed cork screw is rotated to advance along the direction of the current through a conductor, then the direction of rotation of the screw gives the direction of the magnetic lines of force around the conductor.

Magnetic Field around a Straight Conductor Carrying Current

A smooth cardboard with iron filings spread over it, is fixed in a horizontal plane with the help of a clamp. A straight wire passes through a hole made at the centre of the cardboard.

A  current  is  passed  through  the  wire  by connecting  its  ends  to  a  battery.  When  the cardboard is gently tapped, it is found that the iron filings arrange themselves along concentric circles. This clearly shows that magnetic field is developed around a current carrying conductor.

To find the direction of the magnetic field, let us imagine, a straight wire passes through the plane of the paper and perpendicular to it. When a compass needle is placed, it comes to rest in such a way that its axis is always tangential to a circular field around the conductor. When the current is inwards (Fig 3.8a) the direction of the magnetic field around the conductor looks clockwise.

When the direction of the current is reversed, that it is outwards, (Fig 3.8b) the direction of the magnetic pole of the compass needle also changes showing the reversal of the direction of the magnetic field. Now, it is anticlockwise around the conductor. This proves that the direction of the magnetic field also depends on the direction of the current in the conductor. This is given by Maxwell’s rule.

Magnetic Field due to a Circular Loop Carrying Current

A cardboard is fixed in a horizontal plane. A circular loop of wire passes through two holes in the cardboards as shown in figure. Iron filings are sprinkled over the cardboard. Current is passed through the loop and the card board is gently tapped. It is observed that the iron filings arrange themselves along the resultant magnetic field. The magnetic lines of force are almost circular around the wire where it passes through the cardboard. At the centre of the loop, the line of force is almost straight and perpendicular to the plane of the circular loop.

Magnetic Flux

’Flux’ is a word used in the study of the quantity of certain fluid flowing across any surface. Magnetic flux deals with the study of the number of lines of force of magnetic field crossing a certain surface.

Consider an area ‘A’ placed in a magnetic field having magnetic induction ‘B’ at an angle ‘θ’ as shown in figure. The area, in vector notation, can be represented by a vector directed along the normal to the area and having a length proportional to the magnitude of the area. Magnetic flux ‘φ_B’ through area ‘a’ is given by

But, B cosθ = component of B perpendicular to the area ‘a’.

Magnetic flux lined with the surface is defined as the product of area and component of ‘B’ perpendicular to the area.

Case (a):

If θ = 90º, cosθ = 0

When angle between ‘B’ and the normal to the surface is90º, ‘B’ will be parallel to the surface as shown in figure.

So, φ_B = BA0 = 0

No magnetic flux is linked with surface when the field is parallel to the surface.

Case (b):

If θ = 0º, cosθ = 1

In this case ‘B’ is perpendicular to the surface.

(φ_B)_max = BA1 = BA

Magnetic flux linked with a surface is maximum when area is held perpendicular to the direction of field.

Since B = µH

Here, µ is the permeability of the medium and ‘H’ is magnetic intensity, i.e., the number of lines of force per unit area in free space.

(φ_B)max = µαH

In case the magnetic field is not uniform, the magnetic flux φ_B linked with a surface can be obtained as follows.

Let ‘dφ_B’ be the magnetic flux linked with a small area ds of the surface, The area is so small that the field can be considered to be the same over that area.

Here, 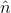 is a unit vector along the outward drawn normal to the surface at that point.

Thus,

Or,

Thus, magnetic flux linked with a surface in a magnetic field is defined as the surface integral of the magnetic flux density over that surface.

Any line of force cutting an electric circuit more than once has its effect multiplied by the number of times it cuts the circuit.

Refer this simulation for closed right hand rule

This illustrates the closed right hand rule used for determining the rotation of a magnetic field generated by a moving positive charge.

Units of Magnetic Flux

In C.G.S. system, unit of magnetic flux is Maxwell and in S.I. system it is weber or tesla per meter square.

1 weber = 10⁸ maxwell
 

Difference between Magnetic Flux and Magnetic Field Strength

Magnetic field strength (H) is the amount of magnetizing force. As stated above, it is proportional to the length of the conductor and the total current passing through the conductor. Hence, magnetic intensity is thus a vector quantity whose magnitude is the strength of a magnetic field at a point in the direction of the magnetic field at that point. The magnetic flux density, denoted by B is also a function of the magnetizing force H.

On the other hand, magnetic flux is the measure of the magnetic field strength of a two dimensional surface, say one particular side of a magnet. In text, it is usually depicted as a cluster of vectors attached to a geometrically abstract surface. Each vector intersects a separate point on the surface.

Watch this Video for more reference
 

Problem (JEE Main)

An electron is projected with velocity v₀ in a uniform electric field E perpendicular to the field. Again it is projected with velocity v₀ perpendicular to a uniform magnetic field B. If r₁ is initial radius of curvature just after entering in the electric field and r₂ is initial radius of curvature just after entering in magnetic field them the ratio r₁/r₂ is equal to

(a) Bv₀²/E              (b) B/E

(c) Ev₀/B               (d) Bv₀/E

Solution:

We know that, qE = mv₀²/r₁

So, r₁ =  mv₀²/qE

and r₂ = mv₀/qB

So, r₁/r₂ = Bv₀/E

Thus, from the above observation we conclude that, option (d) is correct.

Problem:

1000 turns per meter are wound over a Rowland ring of ferromagnetic material. On passing a current of 2 ampere in the coil, a magnetic field of 10 Wb/m² is produced in it. The magnetizing force generated in the material will be:

(A) 1.2 × 10^–3 A/m                (B) 2.6 × 10^–3 A/m

(C) 2.6 × 0^–4 A/m                  (D) 2 × 10³ A/m

Solution: 

We know the formula of magnetizing force.

Hence, using the formula we get,

H= Ni / 2pr = ni = 10³ × 2 = 2 × 10³ 

Hence, answer is (D) 2 × 10³ A/m

Problem:

In the above problem, the value of intensity of magnetization in A/m will be:

(A) 7.96 × 10⁶                        (B) 7.96 × 10^–6

(C) 3.98 × 10³                        (D) zero

Solution: 

(A) B = m₀ (I + H)

I = B / m₀ – H = 10/4p × 10^–7 – 2 × 10³ = 7.96 × 10⁶ A/m

Who first discovered the relationship between electricity and magnetism?

(a) Faraday              (b) Newton

(c) Maxwell              (d) Oersted

Question 2

According to the system international unit the unit of magnetic flux is

(a) weber            (b) tesla

(c) N/C               (d) N/m

Question 3

The magnetic field lines inside a long, current carrying solenoid are nearly

(a) straight          (b) circular

(c) parabolic         (d) elliptical

Question 4

A soft iron bar is introduced inside a current carrying solenoid. The magnetic field inside the solenoid,

(a) will become zero       (b) will decrease

(c) will increase              (d) will remain unaffected

Question 5

The direction of induced current is obtained by

(a) Fleming’s left-hand rule

(b) Maxwell’s right-hand thumb rule

(c) Ampere’s rule

(d)  Fleming’s right-hand rule

Related Resources

• You might like to magnetic moment.

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

• To get answer to any question related to magnetic flux density or magnetic induction click here.