Intersection of a Circle and a Rectangular Hyperbola

 

Rectangular hyperbola is an important concept associated with the hyperbola. The hyperbola in which the length of transverse axis is equal to that of conjugate axis is called a rectangular hyperbola. It is also termed as equilateral hyperbola. 

The eccentricity of the rectangular hyperbola is √2 and the length of its latus rectum is equal to its transverse or conjugate axis.

What happens when a circle intersects with a Rectangular Hyperbola?

A rectangular hyperbola and a circle meet in four points. The mean of these four points is the middle point of the centres of the hyperbola and that of the circle.

Let us explain this concept in detail:

Let the rectangular hyperbola be xy = c² and the equation of the circle be x² + y² + 2gcp + 2fy + k = 0. Any point on the hyperbola is (cp, c/p). If it lies on the circle, then c²p² + c²/p² + 2gcp + 2fc/p + k = 0.

⇒ c²p⁴ + 2gcp³ + kp² + 2fcp + c² = 0.

This is fourth degree equation in p, which has four roots. Hence the circle and the hyperbola intersect in four points. If p₁, p₂, p₃, p₄ are the roots of this equation, then

p₁ + p₂ + p₃ + p₄ = –2gc/c² = –2g/c 

⇒  cp₁ + cp₂ + cp₃ + cp₄ = 2g

⇒ x₁ + x₂ + x₃ + x₄/4 = –g/2

Also 1/p₁ + 1/p₂ + 1/p₃ + 1/p₄ = p₁p₂p₃/p₁p₂p₃p₄ = –2fc/c²/c²/c² = –2f/c

⇒ c/p₁ + c/p₂ + c/p₃ + c/p₄ = –2f 

⇒ y₁ + y₂ + y₃ + y₄/4 = –f/2.

Hence the mean of the four points is (–g/2, –f/2) which is the mid-point of the centre of the hyperbola and that of the circle.

Result:

Hence, if a circle and the rectangular hyperbola xy = c² meet in the four points r₁, r₂, r₃ and r₄, then

(a) r₁r₂r₃r₄ = 1

(b) The centre of the mean position of the four points bisects the distance between the centre of the two curves.

(c) The centre of the circle through the points r₁, r₂ and r₃ is {c/2 (r₁ + r₂ + r₃ + 1/r₁r₂r₃), c/2(1/r₁ + 1/r₂ + 1/r₃ + r₁r₂r₃)}.

Illustration:

A circle and a rectangular hyperbola meet in four points A, B, C and D. If the line AB passes through the centre of the circle, prove that the centre of the hyperbola lies at the mid-point of CD.

Solution:

The line AB passes through the centre of the circle. Hence AB is the diameter of the circle and the mid-point of AB is the centre of the circle. Let the co-ordinates of A, B, C, D be respectively (x₁, y₁), (x₂, y₂), (x₃, y₃) and (x₄, y₄). Let the centres of the hyperbola and the circle be (h, k) and (g, f).

Then (x₁+ x₂ + x₃ + x₄)/4 = (h+g)/2

But g = (x₁+x₂₎/2

⇒ (x₁+ x₂ + x₃ + x₄)/4 = h/2 + (x₁+x₂₎/4

⇒ (x₃ + x₄₎/2 = h

Similarly we can prove that (y₃ + y₄₎/2 = k.

Hence (h, k) is the mid-point of CD.

Result:

We know that the asymptotes of a rectangular hyperbola are mutually perpendicular, but is it possible to find the equation of a hyperbola whose asymptotes are the co-ordinate axes?

Proof:

Let transverse and conjugate axes be the axes of co-ordinates (X’OX and Y’OY in the above figure), then the equation of rectangular hyperbola is

X² – Y² = a²                                                …… (1)

Also we know that the asymptotes of a rectangular hyperbola are at right angles to each other.

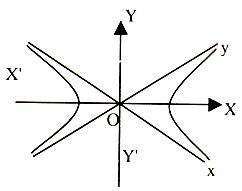
Let Ox and Oy be the asymptotes, each making as angle of π/4 with the co-ordinate axes. Rotate the axes through as angle of π/4 with the co-ordinate axes. To find the equation of the rectangular hyperbola referred to asymptotes as axes. We have to substitute for X and Y in (1) the x cos (–π/4) – y sin (–π/4) and y cos (–π/4) + x sin (–π/4) respectively.

i.e. (x+y)/√2 and (y–x)/√2 respectively.

So from (1) equation of the rectangular hyperbola referred to asymptotes as axes is

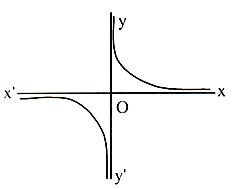
(x+y/√2)² = (y–x/√2)² = a² ⇒ xy = a²/2

⇒ xy = c² where 2c² = a²

Illustration:

PQ and RS are two perpendicular chords of the rectangular hyperbola xy = c2. If O is the centre of the hyperbola, then the product of the slopes of OP, OQ, OR and OS is equal to

(a) -1                                                                                                                                       (b) 1

(c) 2                                                                                                                                        (d) 4

Solution:

Let the parameters exhibited by P, Q, R and S be r₁, r₂, r₃ and r₄.

Now, PQ is perpendicular to RS which implies {(c/t₂ – c/t₁)/ (ct₂ – ct₁)} . {(c/t₃ – c/t₄)/ (ct₃ – ct₄)} = -1

On simplification, it yields t1t2t3t4 = -1.

Now, slope of OP = 1/t12

Hence, the product of slopes of OP, OQ, OR and OS = 1/t₁²t₂²t₃²t₄² = 1/1 = 1.
 

Related Resources

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Hyperbola comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.