Important Properties of Hyperbola

Hyperbola is an extremely important topic of IIT JEE Mathematics syllabus. Students are advised to remember all the important properties of hyperbola on their fingertips so as to ace the competitions like the JEE with ease.

Now, we know that hyperbola is a conic whose eccentricity is greater than unity i.e. e > 1.     

The standard equation of hyperbola is x²/a² – y²/b² = 1, where b² = a² (e²-1).

This gives a²e² = a² + b² or e² = 1 + b²/a² = 1 + (C.A / T.A.)².

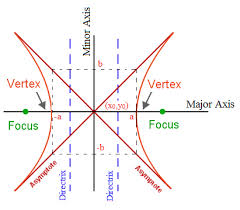
Various important terms and parameters of a hyperbola are listed below:

• There are two foci of a hyperbola namely S (ae, 0) and S’(-ae, 0).

• The equations of directrices are x = a/e and x = -a/e.

• The latus rectum = 2b²/a = 2a (e²-1) and its length is therefore 2e.

• The transverse and the conjugate axis of the hyperbola are together known as principal axis of the hyperbola.

• For a hyperbola with the given equation x²/a² – y²/b² = 1, its conjugate is given by the equation – x²/a² + y²/b² = 1.

• In parametric coordinates, the equations x = a sec θ and y = b tan θ together represent the hyperbola x²/a² – y²/b² = 1, where θ is a parameter. Another set of equations representing the same hyperbola are x = a cosh ∅ and y = b sinh ∅.

For more details, view the following video on hyperbola

Some Important Results and Properties

• Focal Property: The difference of the focal distances of any point on the hyperbola is constant and is equal to transverse axis i.e. ||PS – PS’|| = 2a. The distance SS’ is the focal length.

• If e₁ and e₂ are the eccentricities of the hyperbola and the conjugate hyperbola then this relation holds good: e₁^-2 + e₂^-2 = 1.

• If the lengths of the transverse axis and the conjugate axis are equal then the hyperbola is said to be a rectangular or equilateral hyperbola.

• The eccentricity of the rectangular hyperbola is √2 and the length of its latus rectum is same as its transverse or conjugate axis.

• The point (x₁, y₁) lies within, on or outside the hyperbola if the quantity x₁²/a² – y₁²/b² = 1 is positive, zero or negative.

• The line y = mx + c is a secant, a tangent or passes from the outside of the hyperbola according as c² > = < a²m² - b².

• Equations of tangents: 

1. The equation of tangent to the hyperbola at the point (x₁, y₁) is xx₁/a² – yy₁/b² = 1.

2. In general, two tangents can be drawn to the hyperbola from an external point (x₁, y₁) to the hyperbola and they are given by the equations (y-y₁) = m₁(x-x₁) and (y-y₂) = m₂(x-x₂), where m₁ and m₂ are the roots of the equation (x₁² – a²)m² – 2x₁y₁m + y₁² + b² = 0.

3. In parametric coordinates, the equation of the tangent is given by x sec θ/a – y tan θ/b = 1.

4. Also, y = mx ± √(a²m² – b²) can be taken as a tangent to the hyperbola x²/a² – y²/b² = 1.

5. The portion of the tangent between the point of contact and the directrix subtends a right angle at the corresponding focus. 

• Equations of normals:

1. The equation of the normal to the hyperbola at the point (x₁, y₁) is a²x/x₁ + b²y/y₁ = a²-b² = a²e².

2. In parametric coordinates, the equation becomes ax /sec θ + by/ tan θ = a² + b² = a²e².

• The tangent and normal at any point of hyperbola bisect the angle between the focal radii.

• The asymptotes of a hyperbola and its conjugate are the same.

• Asymptotes are the tangents to the centre.

• The asymptotes pass through the centre of the hyperbola and the axes of the hyperbola are the bisectors of the angles between the asymptotes.

• Rectangular hyperbola:

1. The equation is xy = c² with parametric representation x = ct, y = c/t, t ∈ R – {0}.

2. Equation of the tangent at P(x₁, y₁) is x/x₁ + y/y₁ = 2 and at P(t) is x/t + ty = 2.

3. Equation of normal is y – c/t = t²(x-ct).

• The equation of pair of tangents drawn from a point P(x₁, y₁) to the hyperbola x²/a² – y²/b² = 1 is SS₁ = T², where S = x²/a² – y²/b² -1,  S₁ = x₁²/a² – y₁²/b² – 1, T = xx₁/a² – yy₁/b² - 1.

• The straight line y = mx + c is a tangent to the curve, if c² = a²m² – b². In other words, y = mx + √a²m²–b² touches the curve for all those values of m when m > b/a or m < –b/a.

• The equation of the chord through the points θ₁ and θ₂ is

• Through a given point, four normals (real or imaginary) can be drawn to a hyperbola.

• The tangent drawn at any point bisects the angle between the lines, joining the point to the foci, whereas the normal bisects the supplementary angle between the lines.

• Equation of the director circle is x² + y² = a² – b². That means if a² > b², there would exist several points such that tangents drawn from them would be mutually perpendicular. If a² < b², no such point exist. For a² = b², centre is the only point from which two perpendicular tangents (asymptotes) to the hyperbola can be drawn.

• The equation of the chord of contact is xx₁/a² – yy₁/b² – 1 = 0 or T = 0.

• The equation of the chord bisected at the point (x₁, y₁) is xx₁/a² – yy₁/b² – 1 = x₁²/a² – y₁²/b² – 1 or T = S₁.

• The equation of the diameter bisecting the chords of slope m of the hyperbola x²/a² – y²/b² = 1 is y = b²/a²m.

• The polar of the point P(x₁, y₁) with respect to the hyperbola x²/a² – y²/b² = 1 is T = 0, where T = xx₁/a² – yy₁/b² - 1.

• Polar of the focus is the directrix.

• Locus of the feet of the perpendicular drawn from focus of the hyperbola x²/a² – y²/b² = 1 upon any tangent is its auxiliary circle i.e. x² + y² = a² and the product of the feet of these perpendiculars is b².

• A rectangular hyperbola circumscribing a triangle passes through the orthocentre of this triangle.

• If a circle meets a rectangular hyperbola at four points, then the mean value of the points of intersection is the mid-point of the line joining the centres of circle and hyperbola.

Illustration:

For the hyperbola x²/cos² θ – y²/ sin² θ = 1, which of the following remains constant with change in a? (IIT JEE 2003)

(a) abcissae of vertices                                                                   (b) abcissae of foci

(c) eccentricity                                                                                 (d) directrix

Solution:

The given equation is x²/cos² θ – y²/ sin² θ = 1.

Here, a² = cos² θ and b² = sin² θ.

Now, foci = (± ae, 0), where ae = √a² + b²

Hence, foci are ( ±1, 0) whereas vertices are (± cos θ, 0).

eccentricity ae = 1 or e = 1/cos θ

Hence, this shows that focus remains constant with change in θ.