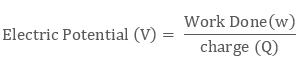Introduction of Electrostatic Potential and Capacitance
Table of Content |
|
|
What is Electrostatic?
Electrostatic is a branch of physics which deals with characteristics electric charges which are slow moving or stationary.
Examples of Electrostatic Phenomenon are:
-
Laser machine and photocopier
-
Spontaneous explosion of grain silos
-
Attraction of paper to a charger scale
In our childhood, we rubbed the scale on our head and try to attract paper from that scale. This is an example of Electrostatic Phenomenon.
Electrostatic Charge
We are familiar with charge flowing through conductors, which we usually just call "electricity". Charge can also be present on insulators and because
these materials do not allow the charge to flow, this
is called Electrostatic Charge
Charges are of two types:
-
Positive Charge
-
Negative Charge
This depends upon the addition or removal of electrons from an atom. If there are more protons than electrons the atom is positively charge and if there are more electrons than protons than the atom is negatively charge.
Fig 1.1 Line of forces for positively and negatively charged particles
Line of Force: A theoretical line in a field of force, such that a tangent at any point gives the direction of the field at that point.
Electrostatic Potential
Inside a field, the amount of work need to move a unit positive charge from one initial point to any specified point without producing any acceleration is known as Electrostatic Potential (or also known as Electric Potential and Electric Field Potential).
Usually the initial or starting point is Earth or a point which is at infinity.
Few points to keep in mind about electric potential are:
-
Electrostatic potential is denoted by V and it is a scalar quantity.
-
Electrostatic potential can be measured in volts.
Coulomb’s Law
The coulomb’s law of electrostatics is also known as Coulomb’s Inverse Square Law which describes the forces acting between the static electrically charged particles.
In its scalar form the law can be written as:

Laws of governing Electrostatics
First Law: The first law states of electrostatic state that ,like charges repel each other while unlike charges attract each other that is two positive charges will repel each other while one positive and one negative charge will attract each other.
Fig 1.2 Like and Unlike Charges
Second Law: The second law states the properties exerted between two point charges:
Fig 1.3 shows two point charge separated by distance d
-
is directly proportional to the product of their strengths.
-
is inversely proportional to the square of the distance between them.
-
is inversely proportional to the absolute permittivity of the surrounding medium.
This is known as Coulomb's Law.
Potential Gradient and Electric Field Intensity
The rate at which electrostatic charge is changed with respect to displacement is known as Potential Gradient.
Electric field intensity is the negative of potential gradient at that point.
Fig 1.5 Potential gradient and electric field intensity for a radial field
Equipotential Surfaces
The surfaces which have equal electrostatic potential at each point are known as Equipotential Surfaces.
Fig 1.4 Equipotential Surface
The work done to move any charge from one place to other place on an equipotential surface is zero as all the points have same potential.
Electric Potential Energy
The potential energy that results from conservative Coulomb forces and is associated with the configuration of a particular set of point charges within a defined system is known as Electric Potential Energy and is measured in joules.
Fig 1.6 Electrostatic potential Energy
Electrostatic Shielding
Electrostatic Shielding is the process of setting apart a certain region of space from external field. It is based on the fact that the electric field in conductor is zero.
Fig 1.7 Electrostatic Shielding
What is Capacitor?
Capacitor also known as Condenser is two terminal electric components which has ability or capacity to store energy in the form of electric charge. The storing capacity of capacitance very from small storage to high storage.
Fig 1.8 Capacitors
Capacitance in Physics
The ability of ancapacitor to store the energy in form of electric charge is known as Capacitance.
In other words, capacitance can be described as the storing ability of an capacitor and it is measured in farads.
For Example, if we connected a capacitor to a 9 volt battery and measured that it stored 9 coulombs of charge, its capacitance would be 1 farad.
Capacitor in Series and in Parallel
In Series
Fig 1.9 capacitors connected in series
Capacitor C1 and C2 are connected in series. When the capacitors are connected serially than the total capacitance that is Ctotal is less any one of the capacitor’s capacitance.
The capacitance of capacitor connected in series can be calculated as:

In Parallel
Fig 1.10 Capacitor connected in parallel
Capacitor C1 and C2 are connected in parallel. When the capacitors are connected parallel than the total capacitance that is Ctotalis any one of the capacitor’s capacitance
The capacitance of capacitor connected in parallel can be calculated as:

Electrical Capacitance
Electrical conductance of a conductor is defined as the capacity to store charge in it. Whenever charge is applied to an insulator its potential is raised to some certain level. Charge on a conductor and its electric potential are both directly proportional to each other. So, as we increase the charge electric potential also increases.
V ∝ Q
Or
Q = C V
C is the proportionality constant
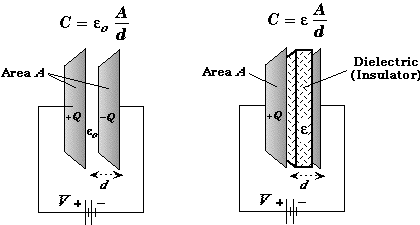
Parallel Plate Capacitor
The setup of dielectric and electrode to form a capacitor is known as parallel plate capacitor.
The two parallel conductive plates (electrodes) are used and in between medium of dielectric. The value of capacitance is dependent on the material or the medium between the two plates
Fig 1.11 Parallel Plate Capacitor
A is the common area of the two plates and d is the distance between the plates.
Capacity of Parallel Plate Capacitor
Cair = ε0A/d
Cmed = Kε0A/d
Here, A is the common area of the two plates and d is the distance between the plates.
Effect of Dielectric on Capacitance of Capacitor
Faraday have given this theory, that is if the space between two electrodes are filled with dielectric the capacitance of the capacitor will be increased.
If all the space is filled by a dielectric that is there is no place left then the capacitance of a capacitor will be increased by K. and here K is known as Dielectric Constant.
Fig 1.12 Effect of Dielectric on Capacitor
Energy Stored on a Capacitor
Energy Stored on a Capacitor can be calculated through following expression:

Energy Density
The total amount of energy per unit volume is known as Energy Density.
Energy density is denoted by U.

Numericals
(Related to coulomb’s law, electrostatic potential)
1. A point charge q = - 8.0 × 10-9 C is placed at the origin. Calculate electric field at a point 2.0 m from the origin on the z-axis.
Given data: Charge = q = -8.0 × 10-8 C
Distance = r = 2.0m
To be found: E =?
Calculations: We know that, by coulomb’s law

Putting values, we get:
E= 180N C-1
Since point is on z-axis
E = 180 NC-1 ќ
2. A particle having a charge of 20 electrons on it falls through a potential difference of 100 volts. Calculate the energy acquired by it in electron volts (eV)
Given Data: Charge = q = 20
e = 20 1.6 10-9 = 32 × 10-19C
Potential difference = ΔV = 100 V
To determine: Energy required in (eV) = E =?
Calculations:
We know that:
E = qΔV
= (32× 10-19)(100)
= 3200 × 10-19 Joules
Since 1eV = 1.6 × 10-19C
= 2000eV
E = 2 × 103 eV
(Related to energy density and parallel plate capacitors)
1. Find the energy density of a capacitor if its electric field, E = 5 V/m.
Given,
E = 5V/m
We know that,
ϵ0 = 8.8541 × 10−12 F/m
The energy density formula of capacitor is given by
U = 1 / 2 ϵ0E2
= 1 / 2 × 8.8541 × 10−12 × 52
U = 1.10×10−10 FV2/m3
2. A parallel plate capacitor is placed in the air has an area of 0.44m22 and are separated from each other by distance 0.04m. Determine the parallel plate capacitor
Given: Area A = 0.44 m22,
distance d = 0.04 m,
relative permittivity k = 1,
ϵo= 8.54 ×10−12 F/m
The parallel plate capacitor formula is given by,

Therefore, the parallel plate capacitor is9.739 × 10-11 F
Watch this Video for more reference
More Readings