Coulomb’s Law
Table of Content |
Introduction to Coulomb’s Law
Every physical phenomenon in the Physics world involves some sort of attractions and repulsions and make the world exist in a special form. It is because of attraction and repulsions between particles that the environment remains in a well-equipped and well balanced environment. If these attractions and repulsions are made to disturb or change they can give astounding results in observations.
For Example, take electrons in an atom, if the attraction between protons in the nucleus and electrons around the shells is disturbed it can even destroy the atom. Physicists have always been interested in discovering the quantitative aspect of Physics as it helps in deepening of concepts and evolving new theories and ideas from them. To find out the extent of repulsion or attraction force between two particles, having some charge, Charles – Augustin de Coulomb provided the Coulomb’s Law.
Coulomb’s Law
Coulomb’s Law is formula or quantitative aspect of electricity which gives an idea about force between two point charges. By the word point charge, we mean that in physics, the size of linear charged bodies is very small compared to the distance between them, so we consider them as point charges as it becomes easy for us to calculate the force of attraction/ repulsion between them.
Charles-Augustin de Coulomb, a French physicist in 1784, measured the force between two point charges and found that the force is inversely proportional to the square of the distance between the charges and directly proportional to the product of charges (magnitudes only).
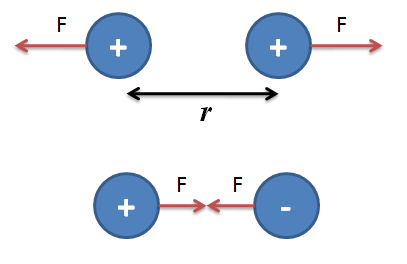
Generally, the statement, let’s say there are two charges q1 and q2. The distance between the charges is ‘r’, and the force of attraction/repulsion between them is ‘F’. Then
F ∝ q1q2
F ∝ 1/r2
F = k q1q2/ r2
where k is proportionality constant and equals to 1/4 π ε0, the symbol ε0 is called epsilon naught and it signifies permittivity of a vacuum.
The value of k comes 9 × 109 Nm2/ C2 when we take the S.I unit of value of ε0 is
8.854 × 10-12 C2 N-1 m-2
Coulomb also stated that like charges repel each other and unlike charges attract each other. This means charges of same sign will push each other with repulsive forces while charges with opposite signs will pull each other with attractive force.
Example:
Two charges 1 C and – 3 C are kept at a distance of 3 m. Find the force of attraction between them.
We have q1 = 1C, q2 = – 3C and r = 3m
Then using Coulomb’s Law and substituting above values we get
F = k q1q2/ r2
F = 9 × 109 × 1 × 3/ 32
F = 3 × 109 Newton
Example:
Two charges q1 and q2 of magnitude 3 C and 4C are kept on two corners of a right-angled triangle with sides 3m, 4m and 5m. Find the force acting on them.
We have q1 = 3 C and q2 = 4C, and r equals to 5m which is the shortest distance between both the charges. Now substituting values accordingly in the relation
F = k q1q2/ r2
F = 9 × 109 × 3 × 4/ 52
F = 4.32 × 109 Newton
Therefore the force of attraction between both the charges will be 4.32 × 109 Newton
Discovery of Coulomb’s Law
Coulomb’s discovered a useful law, which later framed the foundation of electrostatics. Coulomb performed an experiment with the help of torsion balance and two small spheres. The distance between both spheres was quite large as compared to radii of the sphere. This was done to make measurements simple and to consider two spheres as point charges. At that time people didn’t have any idea about charges and their calculations, so to make the formula exist, Coulomb made use of symmetry, for prediction of charges. He stated that if there is charge ‘q’ on a sphere, then by bringing the other sphere in contact, by symmetry charge ‘q’ will be equally divided and each sphere will acquire a charge of ‘q/2’.
Later on, he created several pairs of spheres of charges q/4,q/8 and so on. Then Coulomb varied the distance between fixed pairs of charges and measured the value of force corresponding to them. Comparing forces, he measured in his observations and discovered Coulomb’s Law. Coulomb’s Law also helped in framing a definition of charge, in a new way.
1 Coulomb or 1 C is defined as the charge when placed at a distance of 1m from another charge of space magnitude in a vacuum and experiences a repulsion force of magnitude 9×109 N.
Vector Form of Coulomb’s Law
The physical quantities are of two types namely scalars (with the only magnitude) and vectors (those quantities with magnitude and direction), Force is a vector quantity as it has both magnitude and direction. The Coulomb’s law can be re-written in the form of vectors. Remember we denote vector “F” as F, vector r as r and so on.
Let there be two charges q1 and q2, with position vectors r1 and r2 respectively. Now since both the charges are of the same sign, there will be a repulsive force between them. Let the force on the q1 charge due to q2 be F12 and force on q2 charge due to q1 charge be F21. The corresponding vector from q1 to q2 is r21 vector.
r21 = r2 – r1
To denote direction of a vector from position vector r1 to r2 , and from r2 to r1 as:
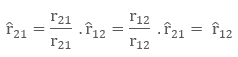
Now, the force on charge q2 due to q1, in vector form will be expressed as:
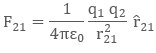
The above equation is the vector form of Coulomb’s Law.
Remarks on Vector Form of Coulomb’s Law
While applying Coulomb’s Law to find out the force between two point charges, we take care of following remarks:
-
The vector form of equation is independent of signs of both the charges, as both the forces are opposite in nature
-
The repulsive force F12 , that is force on charge q1 due to q2 and another repulsive force F21 that is force on charge q2 due to q1 are opposite in signs, due to change in position vector
F12 = - F21
This is because the position vector in case of force F12 is r12 and position vector in case of force F21 is r21, now
r12 = r1 - r2
Since both r21 and r12 are opposite in signs, they make forces of opposite signs too
This proves that Coulomb’s Law fits into Newton’s Third Law i.e. every action has its equal and opposite reaction
-
Coulomb’s Law provides the force between two charges when they’re present in a vacuum. This is because charges are free in a vacuum and don’t get interference from other matter or particles.
Limitations of Coulomb’s Law
Coulomb’s Law is derived under certain assumptions and can’t be used freely like other general formulas. The law is limited to following points:
-
The formula can only be used if the charges are static ( in rest position)
-
The formula is easy to use while dealing with charges of regular and smooth shape, and it becomes too complex to deal with charges having irregular shapes
-
The formula is only valid when the solvent molecules between the particle are sufficiently larger than both the charges
Watch this Video for more reference
More Readings