How to Determine the Photoelectric Current

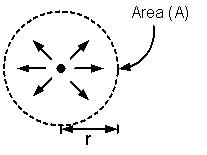
Let P be the power of a point source of electromagnetic radiations, then intensity I at distance r from the source is given by 

I = P/4πr² (W/m²)

If A is the area of a metal surface on which radiations are incident, then the power received by the plate is

P' = IA = P/4πr² (W) 

If f is the frequency of radiation, then the energy of photon is given by 

E = hf

The number of photons incident on the plate per second (called photon flux) is given by

Φ  = P' / E = [P/4πr² × A / hf]

If f > f₀ (threshold frequency) and photon efficiency of the metal plate is η%, then the number of photoelectrons emitted per second is given by

n = Φη/100 [P/4πr² × A / hf]] η/100

Finally, the photocurrent i is given by

i = ne 

Where e is the charge of an electron (e = 1.6 × 10^–19 J)

Illustration 1:

Photoelectric threshold of metallic silver is λ = 3800 Å. Ultra-violet light of λ = 2600 Å is incident on silver surface. Calculate

(i)     the value of work function in joule and in eV.

(ii)    maximum kinetic energy of the emitted photoelectrons.

(iii)    the maximum velocity of the photo electrons (mass of the electron = 9.11 x 10^–31 kg)

Solution:

(i)     I0 = 3800 Å

W = hf₀ = h c/λ₀ = 6.633 × 10^–34 × 3 × 10⁸ / 3800 × 10^–10

J = 6.63 × 10^–34 × 3 × 10⁸ / 3800 × 10^–10    J = 5.23 × 10^–19        J = 3.27 eV

(ii)    Incident wavelength λ = 2600 Å

f = incident frequency = 3 × 10⁸ / 2600 × 10^–10 Hz 

Then T_max = hf – W₀ 

hf = 6.63 × 10³⁴ × 3 × 10⁸ / 2600 × 10^–10 = 6.63 × 3 / 2.6 × 10^–19 J = 7.65 × 10^–19 J = 4.78 eV

T_max = hf – W₀ = 4.78 eV – 3.27 eV = 1.51 eV.

(iii)  T_max = 1/2 mv²_max

∴ v_max = √2T_max / m = √2 × 2.242 × 10^–19 / 9.11 × 10^–31 = 0.7289 × 10⁶ ms^–1

Illustration 2:

Sun gives light at the rate of 1400 Wm^–2 of area perpendicular to the direction of light. Assume λ(sun light) = 6000 Å. Calculate the

(a)    number of photons/sec arriving at 1m² area at that part of the earth, and

(b)    number of photons emitted from the sun/sec assuming the average radius of Earth's orbit is 1.49 x 10¹¹ m.

Solution: 

I = 1400 W / m²;       I = 6000 A

(a)    n/sec = A / E/photon = (1400 × 1) × (6000 × 10^–10) / 6.63 × 10^–34 × 3 × 10⁸ = 4.22 × 10²¹

(b)    n/sec = Power of Sun(W) / E/photon = I × (4R²) × (6000 × 10^–10) / 6.63 × 10^–34 × 3 × 10⁸ = 1.178 × 10⁴⁵

Illustration 3:

An isolated hydrogen atom emits a photon of 10.2 eV. Calculate:

(a)    momentum of photon emitted

(b)    recoil momentum of the atom

(c)    kinetic energy of the recoil atom. Mass of proton = M_p = 1.67 x 10^–27 kg.

Solution:

(a)    momentum (p) = E/c

=> p = 10.2 × 1.6 × 10^–19 / 3 × 10⁸ = 5.44 × 10^–27 kg m/s      

(b)    recoil momentum of atom = p (Law of conservation of momentum)

 => recoil momentum = 5.44 x 10^–27 kg m/s

 (c)    KE = 1/2 mv² (v = recoil speed of atom, m = mass of H-atom)

=> KE = 1/2 (p/m)² = p²/2m

=> KE = (5.44 × 10^–27)² / (2 × 1.67 × 10^–27) = 8.86 × 10^–27 J