Tangent and Normal to a Curve

 

Table of Content

Geometrical Meaning of the Derivative Tangent and Normal to a Curve Length of Tangent and Normal

Geometrical Meaning of the Derivative

The tangent to the curve y = f(x) at the point (x, y) makes an angle y with the positive x-axis. Then dy/dx = tan Ψ. Thus the derivative dy/dx or f'(x) represents the slope of the tangent to the curve at the point (x, y).

Tangent and Normal to a Curve

Having talked at length about (dy/dx)_(x=a), which gives us the slope at any point of curve, the first thing which strikes an aspirant's mind is it's use to find the equation of tangent or normal of the curve at any point on the curve since dy/dx at x = a gives the slope of tangent at any point x = a of a curve y = f(x), so we can put the value of x = a in f(x) and find the corresponding value of y.

The equation of tangent to the curve y = f(x) at point (a, f(a)) is (y - f(a)) = (dy/dx)_(x=a) (x - a) and

Equation of normal is

y - f(a) = 1/(dy/dx)_(x=a) (x - a)

Provided (dy/dx)|_(x=a) ≠ 0

Let us take another curve for explanation.

PT is the tangent to the curve y = f(x) at the point P(x₁, y₁).

PN is the normal to the curve at P.

The slope of the tangent at P(x₁, y₁) is, [dy/dx]_(x1,y1).

The slope of the normal at P(x₁, y₁) is, 1/[dy/dx]_(x1,y1).

Hence the equation of the tangent PT is, y - y₁ = [dy/dx]_(x1,y1) (x - x₁),

and the equation of the normal PN is, y - y₁ = 1/[dy/dx]_(x1,y1) (x - x₁)

or, [dy/dx]_(x1,y1) = 0.

If (dy/dx)_(x1,y1) = 0, then the equation of the normal would be x = x₁.

If the equation of the curve is in the parametric form x = f(t) and y g(t),

Then dy/dx=dy/dt/dx/dt=(g' (t))/(f' (t)).

Thus the equations of the tangent and the normal are

y - g(t) = (g' (t))/(f' (t)) (x - f(t))

and   f'(t)[x - f(t)] + g'(t)[y - g(t)] = 0.
 

Length of Tangent and Normal

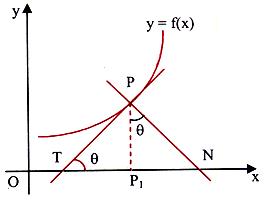
Let P(x, y) be any point on y = f(x). Let the tangent drawn at 'P' meet the 
x-axis at 'T', and normal drawn at 'P' meets the x-axis at 'N'. PT is called the length of the tangent and PN is called the length of the normal.

If 'P₁' be the projection of the point P on the x-axis then TP₁ is called the sub-tangent (projection of line segment PT on the x-axis) and NP₁ is called the sub normal (projection of line segment PN on the x-axis).

Let ∠PTN = q => ∠ P₁PN = q.

We have tan q = dy/dx and PP₁ = y.

Now, PT = y cosec q or,

PT = y√(1+ cot² θ )=y√(1+(dx/dy)² ).

Also, PN = y sec q = y√(1+tan² θ )=y√(1+(dy/dx)² ).

=> Length of the normal, PN = |y| √(1+(dy/dx)² ).

To read more, Buy study materials of Applications of Derivatives comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.