Subtangent and Subnormal

 

Sub tangent and Subnormal

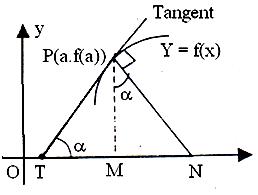
In the figure given above PT' is tangent to the curve at point P of the curve and PN'  is normal. Point T is on x axis where tangent intersects it and point N is on x axis where normal PN'  meets it.

TM'  is called sub-tangent and MN'  is called Subnormal.

From figure

TN'  = PM'  cot a

= (f(a))/(f' (a)) (f'(a) ≠ 0)

Also, MN'  = PM' . tan a

= f(a) . f'(a)
 

Illustration:

Show that the sum of the intercepts of the tangents to the curve 
√x + √y = √a on the coordinate axis is constant.

Solution:

The equation of the curve is √x + √y = √a.

Differentiating with respect to x, we have

1/2 x^-1/2 + 1/2 y^-1/2 dy/dx = 0 => dy/dx=-√(y/x).

The equation of the tangent at (x₁, y₁) is

y - y₁ = √(y₁/x₁ ).

The intercept on the x-axis = √(ax₁ ).

The intercept on the y-axis = √(ay₁ ).

Sum of the intercepts = √(ax₁ ) + √(ay₁ ) = √a (√(ax₁) + √(ay₁))

= a, which is a constant.

Illustration:

The curve = ax³ + bx² + cx + 5 touches the x-axis at P(-2, 0) and cuts the y-axis at a point Q where its gradient is 3. Find a, b, c.

Solution:

Slope of the tangent to the curve at (x₁, y₁) is

[dy/dx]_(x1,y1) = 3ax₁² + 2bx₁ + c

The point Q is (0, 5).

Since the curve passes through (-2, 0),

-8a + 4b - 2c + 5 = 0.                                                         ... (1)

Since the slope of the tangent at (-2, 0) is 0,

12a - 4b + c = 0                                                                 ... (2)

Since the slope of the tangent at (0, 5) is 3,

c = 3.                                                                                ... (3)

From (1), (2) and (3), a = -1/2,b = -3/4, c = 3.

Illustration:

Find the equation of tangent and normal to the curve x² = 8y + 6 at the point (0, - 5/4)

Solution:

Equation of the curve is

x² = 8y + 6

y = (x²-6)/8

Slope of the tangent to the curve at (0, -5/4) is dy/dx at this particular point

dy/dx=2x/8=x/4

at (0, -5/4) dy/dx = 0

equation of tangent at (0, -5/4)

y + y₁ = m(x - x₁)

y + 5/4 = 0(x - 0)

y + 5/4 = 0

Normal is perpendicular to tangent, so slope of normal = - 1/(dy/dx).

Since dy/dx = 0 hence the normal will be parallel to y axis and will pass through (0, - 5/4), hence equation of normal at (0, -5/4) is 

x = 0

To read more, Buy study materials of Applications of Derivatives comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.