Differentiability

 

Table of Content

Differentiability To find the derivative of f(x) from the first Principle Geometrical Interpretation of Differentiability List of Derivatives of Important Functions

Differentiability

Before introducing the concept and condition of differentiability, it is important to know differentiation and the concept of differentiation.

Differential coefficient of a function y= f(x) is written as

d/dx[f(x)] or f' (x) or f ⁽¹⁾ (x) and is defined by

f'(x)= lim_h→0 (f(x+h)-f(x))/h

f'(x) represents nothing but ratio by which f(x) changes for small change in x and can be understood as

f'(x) = lim_?x→0 (? y)/(? x) = dy/dx

Then f'(x) represents the rate of change of y w.r.t. x or in other words f' (x) represents slope of the tangent drawn at point 'x' of the curve f(x).

Let us understand the geometrical meaning of differentiation:

Slope of PQ = y_Q - y_p /y_Q

                = ((y+?y)-y)/((x+?x)-x) or (f(x+?x)-f(x))/((x+?x)-x)

                = ?y/?x = (f(x+?x)-f(x))/?x

Let point Q approach point P, which the curve = y= f(x) i.e. ? x → 0.

Then, we observe graphically that the slope of chord PQ becomes the slope of the tangent at the point P. which is written as dx/dy or f'(x).

        Since, point Q is approaching point P from the Right Hand side, we obtain f'(x⁺) as follows:

        f'(x+)= lim_?x→0  (f(x+?x)-f(x))/?x

(Right hand derivative)

Similarly,

        f' (x^-) = lim_?x→0 (f(x + ? x)-f(x))/(-? x),?x>0

(Left hand derivative)

Note: For a function to be differentiable at x=a, we should have f'(a^-)=f'(a⁺)

i.e. lim_h→0  (f(a-h)-f(a))/(-h) = lim_h→0  (f(a+h)-f(a))/h

 

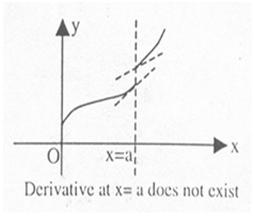
From the above graphs, one must not infer that a curve is non-differentiable only at points of discontinuity. Non differentiability conditions also arise when the curve is continuous and the curve suddenly changes direction. The easiest example of a curve being continuous and non-differentiable is y=|x| at x=0. However when there is a smooth change or gradual change in slope or trajectory of curve, the derivative exists.

Few more illustrations are given below:

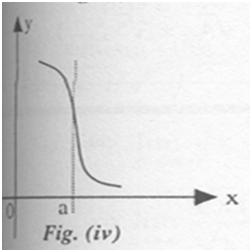
Refer to the following graphs:

 

In figure (i), f'(a) exists and is finite. In figure (ii) both f'(a^-) and f'(a⁺) exist but they are not equal. Hence f'(a) does not exist. Figure (iii) and (iv) have infinite derivatives, i.e. f'(a) = + ∞ and f' (a) = - ∞ respectively. In case of figure (v) we have f'(a) = + ∞ and f'(a⁺) = - ∞ and hence f'(a) does not exist.

 Note:  "Differentiability implies continuity but continuity does not imply differentiability"

Let y = f(x) be continuous in (a, b). Then the derivative or differential coefficient of f(x) w.r.t. x at x ∈ (a, b), denoted by dy/dx or f'(x), is

dy/dx = lim_?x→0 (f(x+?x) - f(x)) /?x                            ..... (1)

provided the limit exists and is finite and the function is said to be differentiable.
 

To find the derivative of f(x) from the first Principle

 If we obtain the derivative of y = f(x) using the formula dy/dx = lim_h→0 (f(x+h)-f(x))/h, we say that we are finding

For example, y = cos 2x.

Here f(x) = cos 2x and

Right Hand Derivative

Right hand derivative of f(x) at x = a is denoted by, Rf'(a) or f'(a⁺) and is defined as

        Rf'(a)= lim_h→0 (f(a+h)-f(a))/h,   h>0

Left Hand Derivative

Left hand derivative of f(x) at x = 1 is denoted by Lf'(a) or f'(a^-) and is defined as

        Lf'(a)= lim_h→0 (f(a-h)-f(a))/(-h),  h>0

Clearly, f(x) is differentiable at x=a if and only if Rf'(a)=Lf'(a).

 

Illustration:

Consider the function

f(x) = 

Since, the function f(x) changes its value at x = 0, there is a possibility of its being non-differentiable at x = 0

Consider,   f'(0⁺) = lim_h→0 (f(0+h)-f(0))/h = lim_h→0 sin (1/h)

                = does not exist

Also, f' (0^-) = lim_h→0 (f(0-h)-f(0))/(-h) = lim_h→0 -sin( 1/h) (does not exist.)

                                => f' (0) does not exist.

Note: lim_h→0 sin 1/h fluctuates between -1 and 1.

 Note: Whenever at x = a, f'(a+) = l₁ (a finite number) and f'(a) = l₂ (a finite number) and if l₁ ≠ l₂, then f' (a) does not exist, but f(x) is a continuous function at x = a.

Illustration:

 A function is defined as follows:

f(x)= Discuss the differentiability of the function at x=1.

Solution:          

We have R.H.D. = Rf'(1) = lim_h→0 (f(1-h)-f(1))/h = lim_h→0 (1+h-1)/h = 1

   and L.H.D. = Lf'(1)= lim_h→0 (f(1-h)-f(1))/(-h)

                 = lim_h→0 ((1-h)³-1)/(-h) = lim_h→0 (3-3h+h² ) = 3

                        ? Rf'(1)≠ Lf'(1)⇒ f(x) is not differentiable at x=1.

Illustration:

Discuss the continuity and differentiability of the function 

f(x)= at x = 0.

Solution: 

Since f'(0^-) ≠ f' (0⁺), f(x) is not differentiable at x=0.
 

Geometrical Interpretation of Differentiability

Geometrically we interpret f' (x)=lim_h→0 (f(x+h)-f(x))/h as the slope of the tangent to the graph of y = f(x) at the point (x, f(x)). Thus if there is no tangent line at a certain point, the function is not differentiable at that point. In other words, a function is not differentiable at a corner point of a curve, i.e., a point where the curve suddenly changes direction. See the following graphs:

 

Note that if a function is discontinuous at the point x = a then three is necessarily a break at that point in the graph of function. So, every differentiable function is continuous but the converse is not true. That is, a continuous function need not be differentiable.

Illustration:

Let: R->R is a function defined by f(x) = max {x, x³}. Find the set of all points on which f(x) is discontinuous and f(x) is not differentiable.

Solution:            

 We have from the graph of y=x and y=x³

                        f(x)= 

Clearly, there is no break in the graph so f(x) is everywhere continuous but there are sudden change of directions at x=-1, 0, 1. So, f(x) is not differentiable at x ∈ {-1, 0, 1}

List of Derivatives of Important Functions

• d/dy (xⁿ ) = nx^(n-1)

• d/dx (cosec x) = -cosec x cot x

• d/dx (x) = 1

• d/dx (e^x ) = e^x

• d/dx (1/x) = -1/x²

• d/dx (ln|x| ) = 1/x

• d/dx (1/xⁿ ) = -n/x⁽ⁿ⁺¹⁾ ,   x>0

• d/dx (sin^-1 x) = 1/√(1-x² )

• d/dx (sin x ) = cos x

• d/dx (cos^-1 x) = 1/√(1-x² )

• d/dx (cos x ) = -sin x

• d/dx (tan^-1 x) = 1/(1-x² )

• d/dx (tan x ) = sec² x

• d/dx (cot^-1 x) = (-1)/(1+x² )

• d/dx (cot x ) = -cosec² x

• d/dx (sec^-1 x) = 1/(|x|√(x²-1))

• d/dx (sec x ) = sec x tan x

• d/dx (cosec^-1 x) = (-1)/(|x|√(x²-1))

To know more about the study material of engineering and medical exams, please fill up the form given below:

Q1.	Q2.	Q3.	Q4.	Q5.
(a)	(a)	(a)	(a)	(a)

To read more, Buy study materials of Limtis and Continuity comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.