Continuity
Table of Content |
Introduction to Continuity

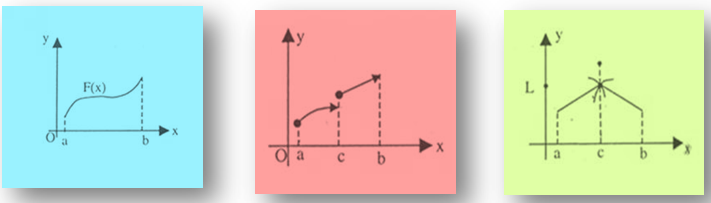
 Continuity is also an important component of differential calculus. Limits and continuity go hand in hand. Both the concepts are quite interrelated and limits lays the groundwork for the concept of continuity. In simple words, the graph of a function is said to be continuous at x = c if while travelling along the graph of the function and in fact even crossing the point x = c whether from Left to Right or from Right to Left, one does not have to lift his pen. The figure drawn on the left shows the graph of a continuous function since it can be made in one flow without lifting the pen and without any sort of breaks.
Continuity is also an important component of differential calculus. Limits and continuity go hand in hand. Both the concepts are quite interrelated and limits lays the groundwork for the concept of continuity. In simple words, the graph of a function is said to be continuous at x = c if while travelling along the graph of the function and in fact even crossing the point x = c whether from Left to Right or from Right to Left, one does not have to lift his pen. The figure drawn on the left shows the graph of a continuous function since it can be made in one flow without lifting the pen and without any sort of breaks.
A function f(x) is said to be continuous at x = a if lim x→a- f(x) = lim x→a+ f(x) = f(a)
i.e. L.H.L. = R.H.L. = f(a) = value of the function at a i.e. lim x→a f(x) = f(a)
If f(x) is not continuous at x = a, we say that f(x) is discontinuous at x = a.
For the function to be continuous at any point x = a, the function must be defined at that point and limiting values of f(x) when x approaches a, is equal to f(a).
Continuity means the function should not have any break or sudden jump at any point in the given domain.
The above three figures clearly illustrate the concept of continuity of a function. The first graph is of a continuous function while the second and third graphs denote discontinuous function.
So the condition for continuity if function at x = a can be defined as L.H.L.= f(a) = R.H.L. i.e.
lim x→a- f(x) = lim x→a+ f(x) = f(a)
i.e. left hand limit is equal to the value of the function at that point and is equal to the right hand limit of the function at that point.
|
|
Hence, a function is said to be discontinuous in any of the following situations:
-
lim x→a- f(x) and lim x→a+ f(x) exist but are not equal.
-
lim x→a- f(x) and lim x→a+ f(x) exist and are equal but not equal to f(a).
-
At least one of the limits does not exist.

Note:
If you are given a function and you are required to comment on the continuity of the function, then instead of attempting to find the limits you should just figure out the points of the domain where the function is not defined. This can help you solve the problem easily and quickly.
Properties of Continuous Functions
Let f(x) and g(x) be functions, both continuous at x = a. Then
-
f(x) + g(x) is continuous at x = a
-
f(x) - g(x) is continuous at x = a.
-
f(x).g(x) is continuous at x = a.
-
f(x)/g(x) is continuous at x = a, provided g(a) ≠ 0.
Continuity in an Interval
A real function 'f' is said to be continuous in an open interval (a, b) if it is continuous at every point in the interval (a, b). Function 'f' is said to be continuous for closed interval [a, b] if it is continuous ∀ x ∈ (a, b) and lim x→a+ f(x) = f(a) and lim x→b- f(x) = f(b)
While solving problems one does not evaluate continuity condition at all points in the interval but uses his elementary knowledge of the function to find points of discontinuity and if none exists then function is continuous in the entire interval.
Let us define a function h(x) given by
h(x) = f(x) for a < x < b
= g(x) for b < x < c
Where f(x) and g(x) are continuous in their respective intervals. Then continuity of h(x) is checked only at x = b, as it is the only point where h(x) changes from f(x) to g(x) and hence is a likely point of discontinuity.

Note:
-
The necessary and sufficient condition for continuity of f at x = a ('a' being finite) is that both lim x→a- f(x) and lim x→a+ f(x) should exist and be equal to f(a).
-
If a function is continuous on a closed interval [a, b], a and b are necessarily finite, it is bounded on it. It may not be always true in case of open interval (a, b).
eg. f(x) = 1/x ∀ 0 < x ≤ 1
The function is continuous but not bounded in the interval (0, 1).
-
f(x) is said to be continuous in an open interval (a, b) if it is continuous at every point in this interval. f(x) is said to be continuous in the closed interval [a, b] if
-
(a) f(x) is continuous in (a, b)
-
(b) lim x→a+ f(x) = f(a)
-
(c) lim x→a- f(x) = f(a)
-

Continuity of some of the common functions
The below table lists some of the important functions with the intervals in which they are always continuous:
|
Functions f(x) |
Interval in which f(x) is continuous |
|
Constant C |
(-∞, ∞) |
|
bn, n is an integer > 0 |
(-∞, ∞) |
|
|x-a| |
(-∞, ∞) |
|
x-n, n is a positive integer. |
(-∞, ∞) – {0} |
|
a0xn + a1xn-1 +........ + an-1x + an |
(-∞, ∞) |
|
p(x)/q(x), p(x) and q(x) are polynomials in x |
R - {x : q(x) = 0} |
|
sin x |
R |
|
cos x |
R R-{(2n-1)π/2 : n = 0, ±1,........} |
|
tan x |
R - {nπ : n = 0, ±1,........} |
|
cot x |
R-{(2n – 1)π/2 : n = 0, ±1, ± 2,........} |
|
sec x |
R – {(2n – 1)π/2 : n = 0, ±1, ± 2,........} |
|
ex |
R |
|
ln x |
(0, ∞) |
Illustration:
Discuss the continuity of
f(x)= 
Solution:
We rewrite f(x) as f(x) = 
As we can see, f(x) is defined as a polynomial function in each of the intervals (-∞, -2). (-2, 0), (0, 3), and (3, ∞). Therefore it is continuous in each of these four intervals.
At the point x = -2
lim x→ -2- f(x)= lim x→ -2 (-x – 1) = 1, and lim x→ -2+ f(x) = lim x→ -2+ (2x + 3) = -1
Therefore, lim x→ -2 f(x) does not exist.
Thus f(x) is discontinuous at x = -2.
At a point x = 0, lim x→0- f(x) = lim x→0+ f(x) = f(0) = 3,
Therefore f(x) is continuous at x = 0.
At a point x = 3, lim x→3- f(x) = lim x→3+ f(x) = f(3) =12
Therefore, f(a) is continuous at x = 3.
So, we conclude that f(x) is continuous at all points in R except at x = -2.
Intermediate Value Theorem
 If f is continuous on the interval [a, b] and f(a) ≠ f(b), then for any value c ∈ (f(a), f(b)), there exists at least one ‘w’ belongs to (a, b) for which f(c) = w.
If f is continuous on the interval [a, b] and f(a) ≠ f(b), then for any value c ∈ (f(a), f(b)), there exists at least one ‘w’ belongs to (a, b) for which f(c) = w.
Note that, continuity through the interval [a, b] is essential for the validity of this theorem.
View the following video on intermediate value theorem:
Extreme Value Theorem
If the function f is continuous on the interval [a, b], then f assumes or takes on a minimum or the least value ‘d’ and a greatest or the maximum value ‘c’ on this interval.
Note:
The extreme value theorem holds good only provided the function in reference is continuous.

Some Important Results
-
If f(x) is continuous and g(x) is discontinuous, then f(x) + g(x) is discontinuous.
-
If f(x) is continuous and g(x) is discontinuous at x = a, then the product f(x) . g(x) may or may not be discontinuous.
-
Even if f(x) and g(x) are both discontinuous at x = a, the product need not necessailry be discontinuous.
-
A continuous function whose domain is a closed interval must have its range also as a closed interval.
-
If a function f is continuous and onto on the closed interval {a, b}, then f -1 is also continuous.
-
If f(a) and f(b) possess opposite signs then there exists at least one solution of the equation f(x) = 0 in the open interval (a, b) provided f is continuous in {a, b}.
Continuity of Composite Functions
If the function u = f(x) is continuous at the point x = a, and the function y = g(u) is continuous at the point u = f(a), then the composite function y = (gof)(x) = g(f(x)) is continuous at the point x = a.
Illustration:
Find the points of discontinuity of y = 1/(u2 + u - 2) where u = 1/(x-1)
Solution:
The function u = f(x) = 1/(x-1) is discontinuous at the point x = 1.
The function y = g(u) = 1/(u2 + u – 2) = 1/(u + 2)(u – 1) is discontinuous at u = -2 and u = 1.
⇒1/(x-1) = -2
⇒ x = 1/2
⇒1/(x-1)=1
⇒x=2
Hence the composite function y = g(f(x)) is discontinuous at three points
x = 1/2, x = 1 and x = 2.
Continuity of functions in which signum function is involved
 The figure shown here is that of a signum or sign function. This function, as we know is defined as
The figure shown here is that of a signum or sign function. This function, as we know is defined as
sgn (x) = 1, x > 0
= 0, x = 0
= -1, x < 0
Hence, the signum function as defined above is clearly discontinuous at x = 0 but is continuous elsewhere.
In general, we can say that f(x) = sgn (s(x)) is discontinuous at x = a if s(a) = 0.
Illustration:
let f(x) = x + a, if x < 0
= |x – 1|, if x ≥ 0
and g(x) = x + 1, if x < 0
= (x-1)2 + b, if x ≥ 0
Where a and b are non-negative real numbers. Determine the composite function gof. If (gof)(x) is continuous for all real x determine the values of a and b. (IIT JEE 2002)
Solution:
(gof)(x) = f(x) + 1, if f(x) < 0
= (f(x) -1)2 + b, if f(x) ≥ 0
Hence, (gof)(x) = x + a + 1, if x < 0
= (x + a – 1)2 + b, if –a ≤ x < 0
= (|x-1| - 1)2 + b, if x ≥ 0
As (gof)(x) is continuous at x = -a,
(gof)(-a) = (gof)(-a+) = (gof)(-a-)
So, 1 + b = 1 + b = 1 hence, this gives b = 0.
Also, gof is continuous at x = 0
So, gof(0) = gof(0+) = gof(0-)
So, b = b = (a – 1)2 + b
Hence, a = 1.


Q1. For a signum function, which of the following statement is true?
(a) It is discontinuous at x = 0 but is continuous elsewhere
(b) It is continuous everywhere.
(c) It is discontinuous everywhere.
(d) none of above.
Q2. If f(a) and f(b) possess opposite signs then there exists at least one solution of the equation f(x) = 0 in
(a) the open interval (a, b)
(b) the open interval (a, b) provided f is continuous in {a, b}.
(c) the closed interval [a, b]
(d) none of above.
Q3. The domain in which xn, n is a positive integer is continuous is
(a) It is discontinuous at x = 0 but is continuous elsewhere
(b) (-∞, ∞)
(c) (-∞, ∞) – {0}
(d) only 0.
Q4. Which of the following statements correctly describe the relationship between limits and continuity?
(a) Existence of limit at x = a ⇒ Continuity at the point x = a and conversely.
(b) Existence of limit at x = a ⇒ Continuity at the point x = a
(c) Continuity at the point x = a ⇒ existence of limit at x = a and the converse also holds good.
(d) Continuity at the point x = a ⇒ existence of limit at x = a but not the converse.
Q5. Which of the following pair of functions are always continuous?
(a) signum and greatest integer function
(b) greatest integer function and polynomial functions
(c) point functions and signum functions
(d) polynomial functions and exponential functions.
|
Q1. |
Q2. |
Q3. |
Q4. |
Q5. |
|
(a) |
(b) |
(c) |
(d) |
(d) |
Related Resources
-
You may wish to refer Types of Discontinuities.
-
Click here to refer the most Useful Books of Mathematics.
-
For getting an idea of the type of questions asked, refer the previous year papers.
To read more, Buy study materials of Limtis and Continuity comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.
View courses by askIITians


Design classes One-on-One in your own way with Top IITians/Medical Professionals
Click Here Know More

Complete Self Study Package designed by Industry Leading Experts
Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child
Click Here Know More