Focal Chord of Parabola

 

Table of Content

Intersection of a Straight Line with a Parabola Chord with a given middle point Focal Chord of a Parabola Length of the chord Position of a point relative to a Parabola Related Resources

Intersection of a Straight Line with a Parabola

The combined equation of straight line y = mx + c and parabola y² = 4ax gives us the co-ordinates of point(s) of their intersection.

The combined equation m²x² + 2x (mc – 2a) + c² = 0 will give those roots. The straight line therefore meets the parabola at two points. 

Points of intersection of y² = 4ax and y = mx + c are given by (mx+c)² = 4ax i.e. m²x² + 2x(mc – 2a) + c² = 0. …… (i) 

Since (i) is a quadratic equation, the straight line meets the parabola in two points, real, coincident, or imaginary. The roots of (i) are real or imaginary according as {2(mx – 2a)}² – 4m²c² is positive or negative, i.e. according as – amc + a² is positive or negative, that is, according as mc is less than or greater than a, (taking a as positive). 

Note: 

When m is very small, one of the roots of equation (i) is very large; when m is equal to zero, this root is infinitely large. Hence every straight line parallel to the axis of the parabola meets the curve in one point at a finite distance and in another point at an infinite distance from the vertex. It means that a line parallel to the axis of the parabola meets the parabola only in one point. 
 

Chord with a given middle point

Equation of the chord of the parabola y² = 4ax whose middle point is (x₁, y₁) is 

(y-y₁) = 2a/y₁(x-x₁)

This can be written as T = S₁, where T = yy₁ – 2a(x+x₁) and S₁ = y₁² – 4ax₁.
 

Focal Chord of a Parabola

The chord of the parabola which passes through the focus is called the focal chord.

Any chord to y² = 4ax which passes through the focus is called a focal chord of the parabola y² = 4ax. 

Let y² = 4ax be the equation of a parabola and (at², 2at) a point P on it. Suppose the coordinates of the other extremity Q of the focal chord through P are (at₁², 2at₁).

Then, PS and SQ, where S is the focus (a, 0), have the same slopes

⇒ (2at-0)/(at²- a) = (2at₁ - 0)/(at₁² - a)

⇒ tt₁² – t = t₁t² – t₁

⇒ (tt₁ + 1) (t₁ – t) = 0.

Hence t₁ = –1/t, i.e. the point Q is (a/t², –2a/t).

The extremities of a focal chord of the parabola y² = 4ax may be taken as the points t and –1/t. 
 

Length of the chord 

The abscissae of the points common to the straight line y = mx + c and the parabola y² = 4ax are given by the equation m²x² + (2mx – 4a) x + c² = 0. 

= 4(mc-2a)² / m⁴ – 4c²/m² = 16a(a-mc)/ m⁴ and (y₁ – y₂) = m(x₁-x₂)

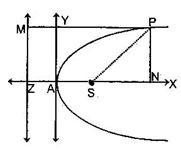
Focal Distance of a Point 

The focal distance of a point P on the parabola

y² = 4ax is the distance between the point P and the focus S, i.e. PS. Thus the focal distance of P = PS = PM = ZN = ZA + AN = a + x.

or PS = a + at² = a(1 + t²). 
 

Position of a point relative to a Parabola 

Consider the parabola y² = 4ax. 

If (x₁, y₁) is a given point and y₁² – 4ax₁ = 0, then the point lies on the parabola. But when y₁² – 4ax₁ ≠ 0, we draw the ordinate PM meeting the curve in L. Then P will lie outside the parabola if PM > LM, i.e., PM² – LM² > 0. 
Now, PM² = y₁² and LM² = 4ax₁ by virtue of the coordinates of L satisfying the equation of the parabola. Hence, the condition for P to lie outside the parabola becomes y₁² – 4ax₁ > 0. 

Similarly, the condition for P to lie inside the parabola is y₁² – 4ax₁ < 0.

Illustration: 

Find the Length of the chord intercepted by the parabola y² = 4ax from the line y = mx + c. Also find its mid-point.

Solution: 

Simply by applying the formula of length of the line joining (x₁, y₁) and (x₂, y₂) we get, 

Length of the chord = √((x₁-x₂)² + (y₁-y₂)² ) 

= √((x₁-x₂)² + m²(x₁-x₂)²) 

= |x₁ – x₂|√(1+m² ) = 4√(a(a-mc)) √(1+m² ) 

[ ? x₁ + x₂ = (-2(m-2a))/m² and x₁x₂ = c²/m² ] 

The midpoint of the chord is ((2a-mc)/m², 2a/m)

Illustration: 

Prove that the circle with any focal chord of the parabola y² = 4ax as its diameter touches its directrix. 

Solution: 

Let AB be a focal chord. If A is (at², 2at), then B is (a/t² ,-2a/t). 

Equation of the circle with AB as diameter is 

(x – at²) (x-a/t²) + (y – 2at) (y + 2a/t) = 0. 

For x = –a, this gives (a² (1 + t² )2)/t² + y² – 2ay (t-1/t) – 4a² = 0. 

⇒ a² (t-1/t)2 + y² – 2ay(t – 1/t) = 0 

⇒ [y – a(t – 1/t)]2 = 0, which has equal roots. 

Hence x + a = 0 is a tangent to the circle with diameter AB.

Illustration: 

Find the locus of the centre of the circle described on any focal chord of a parabola as diameter. 

Solution: 

Let the equation of the parabola be y² = 4ax. 

Let t₁, t₂ be the extremities of the focal chord. Then t₁ . t₂ = – 1. 

The equation of the circle on t₁, t₂ as diameter is 

(x – at₂²) (x – at₂²) + (y – 2at₁) (y – 2at2) = 0 

or x² + y² – ax (t₁² + t₂²) – 2ay (t₁ + t₂) + a² t₁² t₁² + 4a² t₁t₂ = 0 

⇒ x² + y² – ax (t₁² + t₂²) – 2ay (t₁ + t₂) – 3a² = 0. (? t₁t₂ = –1) 

If (α,β) be the centre of the circle, then α = a/2 (t₁²+t₂² ) If (α, β) be the centre of the circle, then α = a/2 (t₁²+t₂²) 

β = a (t₁ + t₂) ⇒ (t₁ + t₂)² = β²/a² ⇒ t₁² + t₂2 + 2t1t2 =β2/a2 ⇒ 2α/a-2= β2/a2 

⇒ 2aα – 2a² = β² ⇒ β² = 2a (α – a). 

Hence locus of (α, β) is y² = 2a(x – a). 
 

Related Resources

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

• Fast Track your revision with the ultimate Revision Notes on Parabola.

To read more, Buy study materials of Parabola comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.